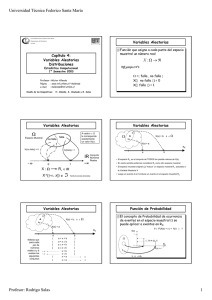
Introducción a las distribuciones de probabilidad.

Distribuciones de probabilidad.
A pesar de la variedad y diversidad de experiencias en el marco de la probabilidad, existen
situaciones reales que por su similitud se pueden agrupar definiendo un modelo teórico,
llamado distribución de probabilidad. Es decir, los procesos reales se modelizan mediante
distribuciones de probabilidad que posteriormente se aplicarán en las más variadas ramas del
conocimiento, en la biología, la psicología, la física o las finanzas.
Las distribuciones de probabilidad trabajan con variables aleatórias , que por ser funciones, nos
permiten desarrollar sobre ellas nuestros conocimientos de análisis: continuidad, derivabilidad,
integración..etc.
Las variables aleatorias se dividen en dos grandes grupos, las variables aleatorias discretas, y
las variables aleatorias continuas que estudiaremos representandolas en los dos grandes
modelos, la distribución binomial o de Bernoulli y la distribución normal o de Gauss. Por último
veremos como ambas se relacionan mediante la aproximación de la binomial a la normal.
Distribuciones de
probabilidad
Variable aleatoria
Variable aleatoria
discreta
Función de
probabilidad
Variable aleatoria
continua
Función de
distribución
Función de
densidad
Distribución Binomial
B(n,p)
Función de
distribución
Distribución Normal
N(0,1) – N(μ,σ)
Aproximación
de la Binomial
a la Normal
1 . Variable aleatoria
Para poder utilizar los métodos propias de las matemáticas y realizar un estudio numérico de
los problemas de probabilidad,es necesario “cuantificar” los resultados de los experimentos
aleatorios, esto es asignar a cada resultado de un experimento aleatorio un número.
Esto siempre es posible, variando en cada caso el criterio prefijado, aunque en un principio no
parezca sencillo daremoos algunos ejemplos en los que establecemos una aplicación,
correspondencia o función entre cada uno de los elementos del espacio muestral asociado a un
experimento y un subconjunto de números reales.
Ejemplo 1:
Sea el experimento aleatorio: lanzamiento de dos monedas. El espacio muestral asociado sería
E= {(C,C),(C, X), (X, C), (X, X)}. Si elegimos la correspondencia entre cada uno de los cuatro
elementos del espacio muestral y el número de caras obtenidas podemos representar el
siguiente gráfico y habremos construido una variable aleatoria.
E
R
11.02
(C,C)
(C,X)
(X,C)
(X,X)
2
1
0
Ejemplo 2:
Sea el experimento aleatorio: selección de un alumno de 2º de BACH de CCSS y estudio de su
talla. El espacio muestral asociado estaría compuesto por los 30 alumnos que componen la
sección y todas las posibles alturas de cada uno de ellos serán los números reales que les
vamos a asociar mediante la correspondencia o función. En este caso observamos que la
representación mediante un gráfico no es tan sencilla como en el caso anterior pues en
principio la altura de estos alumnos puede ser cualquier valor comprendido entre el valor
extremo inferior y extremo superior del intervalo en el que estarán comprendidas las alturas de
los 30 alumnos de la clase.
Dado un experimento aleatorio de espacio muestral E, se llama variable aleatoria (v.a.) a la
correspondencia, aplicación o función matemática que establecemos entre los elementos
del espacio muestral E y cualquier subconjunto de los números reales
Como vemos en los anteriores ejemplos y por comparación con las variables estadísticas
podemos diferenciar dos tipos de variables aleatorias:
Variable aleatoria discreta : que cómo ocurre en el ejemplo 1 sólo puede tomar un número finito
de valores(para mayor rigor convendría afirmar infinito numerable, pero este concepto lo
dejaremos para lecciones venideras.
Ejemplos:
X= A cada individuo de una población le asigna el número de hermanos que tiene.
Y= En el lanzamiento de dos dados, a cada una de las posibilidades del espacio muestral le
asigna el valor de la suma de puntos obtenida.
Z= En un examen de diez preguntas al examen de cada alumno se le asigna los valores del
número de respuestas correctas.
Variable aleatoria continua: que cómo ocurre en el ejemplo 2 puede tomar, al menos
teóricamente, los infinitos valores de un intervalo de 