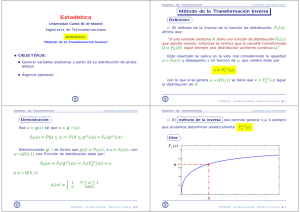
Método de la Transformación Inversa

Estadı́stica
Universidad Carlos III de Madrid
Ingenierı́a de Telecomunicaciones
APÉNDICE:
“Método de la Transformación Inversa”
OBJETIVOS:
• Generar variables aleatorias a partir de su distribución de probabilidad
• Algunos ejemplos
Estadı́stica - Ing. Telecomunicaciones
Universidad Carlos III de Madrid
Método de la Transformación Inversa
Definición:
El método de la inversa de la función de distribución,
afirma que:
FX (x ),
“si una variable aleatoria X tiene una función de distribución FX (x )
que admite inversa, entonces se verifica que la variable transformada
= FX (X ) sigue siempre una distribución uniforme continua .”
U
u
U
Este resultado se aplica en la vida real considerando la igualdad
= FX (x ) y despejando x en función de u , que vendrá dado por
x = FX 1(u )
con lo que si se genera
la distribución de X .
u U (0; 1) se tiene que x = FX 1(u ) sigue
APÉNDICE - Variables Aleatorias: “Método de la Inversa” # 1
Estadı́stica - Ing. Telecomunicaciones
Demostración:
Sea
Universidad Carlos III de Madrid
u = g (x ) tal que x = g
1
(u ):
FU (u ) = P (U u ) = P (X g
1
(u )) = FX (g
Seleccionando g ( ) de forma que g (x ) = FX (x ), o
(0; 1) con Función de distribución dada por:
uU
FU (u ) = FX (g
y
1
(u )) = FX (FX 1(u )) =
1
(u ))
u = FX (x ), con
u
u U (0; 1)
fU (u ) =
1
0
0
u1
resto
APÉNDICE - Variables Aleatorias: “Método de la Inversa” # 2
Estadı́stica - Ing. Telecomunicaciones
Universidad Carlos III de Madrid
El método de la inversa nos permite generar v.a.’s siempre
que podamos determinar analı́ticamente
FX 1(u )
.
Idea:
FX (x)
1
0.8
u
0.6
0.4
0.2
0
x
APÉNDICE - Variables Aleatorias: “Método de la Inversa” # 3
Estadı́stica - Ing. Telecomunicaciones
Universidad Carlos III de Madrid
Algunos ejemplos
Ej1: Generación de v.a’s exponenciales:
E
Recordemos que la función de distribución de una v.a. Exponencial
xp() viene dada por
FX (x ) =
0
e
1
x
x <0
0x y >0
Por el método de la inversa tenemos que considerando la igualdad
u = FX (x ), tenemos que para 0 x , se verifica que:
e
1
1
1
log(1
x = u
u=e
u) = x
x
APÉNDICE - Variables Aleatorias: “Método de la Inversa” # 4
Estadı́stica - Ing. Telecomunicaciones
Universidad Carlos III de Madrid
Por tanto, podemos generar variables exponenciales generando
y después calculando
x=
1
log(1
u
u)
Veremos cómo en la práctica 2 de MATLAB.
APÉNDICE - Variables Aleatorias: “Método de la Inversa” # 5
Estadı́stica - Ing. Telecomunicaciones
Universidad Carlos III de Madrid
Ej2: Generación de v.a.’s Weibull
Ahora supongamos que estamos interesados en generar v.a.’s
X Weibull(; )
que representan por ejemplo el tiempo de vida de un componente
electrónico. Y que tiene como función de distribución
FX (x ) =
donde
1
e
0
(x= )
x >0
0x
; > 0 son parámetros dados.
APÉNDICE - Variables Aleatorias: “Método de la Inversa” # 6
Estadı́stica - Ing. Telecomunicaciones
Universidad Carlos III de Madrid
Nuevamente, mediante el método de la inversa, tenemos que considerando u = FX (x )
e
e
1
(x= )
=
(x= )
=1
(x= ) =
u
u
u)
x= = [ ln(1 u )] x = [ ln(1 u )] :
ln(1
1
1
Por tanto, generando
x = [
u )] u U (0; 1)
y aplicando la transformación
1
ln(1
, obtendremos variables aleatorias Weibull.
APÉNDICE - Variables Aleatorias: “Método de la Inversa” # 7