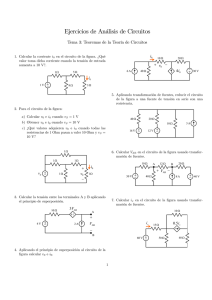
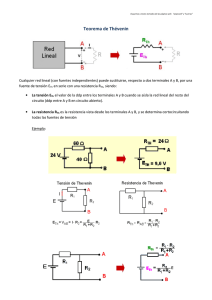
EQUIVALENTE DE THEVENIN

EQUIVALENTE DE THEVENIN
Elemento variable
(carga RL)
Circuito simplificado
Objetivo: Simplificar al máximo un circuito eléctrico el cual alimenta a una carga
(por lo general variable) para facilitar de esta manera su análisis
El circuito simplificado consiste en una fuente de voltaje (VTH)
en serie con una resistencia(RTH)
Aplicaciones:
*Analizar el comportamiento de una carga variable (RL)
*Determinar el valor de carga (RL) con el cual se logrará
la máxima transferencia de potencia
*Calcular las corrientes de corto circuito en redes eléctricas
CASO 1. Fuentes independientes y Resistencias
1.- Determinar el voltaje de circuito abierto entre a y b mediante
cualquier técnica de análisis(nodos, mallas, superposición)
-VS – R1IS + Vab = 0
Vab = Voc = VTH = VS + R1IS
2.- Calcular la Req entre las terminales a y b con las fuentes apagadas
(Fuentes de corriente en circuito abierto, fuentes de voltaje en corto)
R eq = R
TH
= R1 +R2
CASO 2. Fuentes independientes, controladas y Resistencias
1. Calcular el voltaje de Thévenin, mediante cualquier técnica
de análisis( la más conveniente de acuerdo a los elementos)
IX =IS
-R1IS – KIS + Vab = 0
Vab = (R1 + K)IS = Voc =VTH
2. Calcular la corriente de corto circuito(ISC) que circularía de a a b
si el elemento se reemplaza por un corto circuito
IA = IS
IA = IX + IB
I X = I A – IB
L.V.K.
-R1(IA – IB) – K(IA - IB) + R2IB = 0
(R1 + R2 +K)IB = (R1 + K)IA = (R1 + K)IS
IB =
R1 + K
Is = Isc
R1 + R 2 + K
3. Calcular la resistencia de Thévenin como el cociente entre
VTH e ISC
R TH =
Voc
Isc
=
( R 1 + K ) Is
R1 + K
R1 + R 2 + K
= R1 + R 2 + K
Is
CASO 3. Fuentes controladas y Resistencias
Circuito Pasivo == > VTH = 0 V
Para calcular la resistencia de Thévenin, el circuito debe ser
excitado con una fuente de 1V ó 1A (lo que resulte más apropiado de acuerdo
a los componentes del circuito ) y calcular la RTH como el cociente entre Vab e Is
Si se aplica una fuente de 1V
calcular la corriente que esta entrega.
Si se aplica fuente de 1A, calcular el
voltaje entre sus terminales
Ejemplo
a
b
En este caso conviene aplicar una fuente de voltaje ya que
de esta manera ,la variabl e de control (V1) queda definida
V1
V 2 −V1
R2
+
V2
R3
+ KV 1 = 0 ⇒ V 2
= R2
1
R2
Is =
V1
R1
+
RTH =
V1 −V 2
R2
1
Is
− KV 1
+
1
R3
TEOREMA DE MAXIMA TRANSFERENCIA DE POTENCIA
2
 VTH

PL = 
 [RL ]
(
+
)
R
R
 TH
L 
RTH
a
VTH
RL
2
2
dPL  ( RTH + RL ) 2 (VTH ) − (VTH )[2]RL ( RTH + RL ) 
=
=0
dRL 
( RTH + RL ) 4

( RTH + RL ) 2 = [2]RL ( RTH + RL )
b
RL = RTH
Para lograr máxima transferencia de potencia a la carga, el valor
de RL debe ajustarse a un valor igual a la resistencia de Thévenin (RL = RTH)
Para esta condición (RL = RTH)
2
VTH
PL =
4 RTH