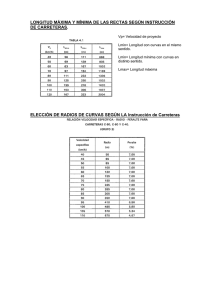
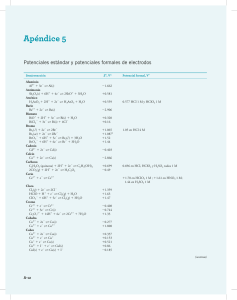
dW dt =P = 2 3 z2e2 c3 v˙2 = dW dr r˙ dW dr = 2 3 z2e2 c3 v˙2 v
Anuncio

Problema 1. Una partícula no relativista de carga ze, masa m y energía cinética E efectúa una colisión frontal con un campo central de fuerza fijo de tipo finito. La interacción es repulsiva y viene descrita por un potencial V (r), que se hace mayor que E a distancias próximas. a) Demuestre que la energía total radiada viene dada por 4 z 2e 2 q m ∆W = 3 m2c3 2 Z ∞ rmin dV 2 dr p dr V (rmin ) − V (r) donde rmin es la distancia mínima al centro de fuerzas. b) Si la interacción es un potencial de Coulomb V (r) = total radiada es: 8 zmv05 ∆W = 45 Zc3 v0 es la velocidad de la carga en el infinito. dW 2 z 2e2 2 dW =P = v̇ = ṙ dt 3 c3 dr dW 2 z 2e2 v̇ 2 = 3 c3 v dr 1 z Z e2 , r demuestre que la energía 1 v̇ = − V ′(r) r m 1 2 E = mv 2 + V (r), v = (E − V (r)) 2 m v=0 con r = rmin, E = V (rmin) 2 z 2e2 ∆W = 3 2 3c m Z ∞ ′ 2 (V (r)) dr q 2 = 2 rmin V rmin − V (r) m q 4 z 2e2 m 3 c3m2 2 Z ∞ (V ′(r))2dr q rmin V rmin − V (r) m v̇ = −V ′(r), Potencial de Coulomb:V (r) = A= Z ∞ rmin zZe2 r r −4dr q E− zZe r u = r −1, , 2 2 du = −r −2dr A= Z umin du √ 0 5 2 2 u 16 · E = 15 · (zZe2)3 E − zZe2u 5 q 4z e m 16 · E 2 ∆W = 3 2 (zZe2)2 = 2 3 3c m 2 15 · (zZe ) 64 z q m 52 E 3 2 45 c m Z 2 1 E = mv02 2 3 64 z m 5 8 zm 5 ∆W = v = v 45 c3m2Z 8 0 45 c3Z 0 2 2 Problema 2. Mostrar que e+ + e− → γ no se puede dar en el vacío. + k µ = p− µ + pµ k 2 = 0 = (p−)2 + (p+)2 + 2p−.p+ = −2m2c4 + 2p−.p+ p−.p+ = m2c4 Evaluemos p−.p+ en el sistema propio del electrón: ~ p .p = 0, imc (p ~ +, iE+/c) = −mE+, E+ < 0 − + 3 1 Reacciones Nos interesa estudiar procesos del tipo M → m1 + m2. En el sistema de laboratorio(L) la partícua M está en reposo. La conservación de momentum implica: ~p1 = ~p = −p ~2 La conservación de la energía: p p 2 2 M = ~p + m1 + ~p 2 + m22 (1) El decaimiento se puede dar sólo si: ∆M = M − m1 − m2 > 0 A partir de (1) se puede encontrar ~p 2. Sin embargo es más simple usando covarianza. Sea P = p1 + p2 4 Consideremos : (P − p1)2 = p22 = −m22 = −M 2 − 2P .p1 − m21 = −M 2 + 2ME1 − m21 M 2 + m21 − m22 E1 = 2M M 2 + m22 − m21 E2 = 2M K i = E i − mi = ∆M m ∆M 1 − i − 2M M Ejercicio 1. π → µ + ν̄ . M = 139.6 Mev,m µ = 105.7 Mev, mν̄ = 0 Problema 3. Límite GZK p + γ → p + π0 Encuentre la energía mínima del protón de tal manera que al interactuar con un fotón del fondo de radiación cósmica, cree un pión en reposo en el sistema propio del protón. 5