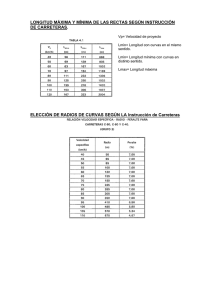
DESTILACIÓN MULTICOMPONENTES F-U-G Métodos Cortos Dr. Edgar Omar Castrejón González INGENIERÍA QUÍMICA Algoritmo INICIO Alimentación especificada Especificar las escisiones de dos componentes clave Determinar la presión de la columna y tipo de condensador, Pb y Pr Repetir solamente si las escisiones estimadas y calculadas de los componentes no clave difieren considerablemente Aplicar Flash (adiabático) a alimentación para presión de columna Calcular Nmin (Fenske) Calcular las escisiones de los componentes no clave A continuación A Calcular la relación de reflujo mínima (Underwood) Calcular el número de etapas teóricas para Roperación (Guilliland) Calcular la localización de la etapa de alimentación (Kirkbride) Calcular los servicios del condensador y del ebullidor FIN Ecuación de Fenske, Nmin Balance de materia, etapa N VN 1 y N 1 LN 1 x N 1 LN x N VN y N LN 1 VN y x N 1 y N VN 1 LN y y N 1 x N Ecuación de equilibrio, etapa 1 yi ,1 K i ,1 x i ,1 para yi , j yi ,2 K i ,2 x i ,2 siendo , yi ,1 x i ,2 yi ,2 K i ,2 K i ,1 x i ,1 x i ,3 x K x yi ,3 K i ,3 K i ,2 K i ,1 x i ,1 i ,2 i ,1 i ,1 Ecuación de Fenske, Nmin Generalizando para etapa N yi ,N K i ,N K i ,N 1 ...K i ,2 K i ,1 xi ,1 (1) Para el componente j y j ,N K j ,N K j ,N 1 ...K j ,2 K j ,1 x j ,1 (2) Dividiendo (1) entre (2) yi ,N K i ,N K i ,N 1 ...K i ,2 K i ,1 x i ,1 x i ,1 i , j ,N i , j ,N 1 ... i , j ,2 i , j ,1 y j ,N K j ,N K j ,N 1 ...K j ,2 K j ,1 x j ,1 x j ,1 Despejando y sabiendo que x N 1 y N xi ,N 1 x j ,1 i , j ,N i , j ,N 1 ... i , j ,2 i , j ,1 x j ,N 1 xi ,1 N N min k 1 k Ecuación de Fenske, Nmin Donde i = Ligero clave (LK) j = Pesado clave (HK) Desventaja: Se deben conocer las condiciones de cada etapa (P, T, xi, yi) para conocer las Ki Suponiendo volatilidades constantes xi ,N 1 x j ,1 N min x j ,N 1 xi ,1 Despejando Nmin m ( i , j ) N ( i , j )1 N MIN xi ,N 1 x j ,1 log xi ,1 x j ,N 1 log i , j 1/2 N MIN di bj log bi d j log m Distribución de componentes no-clave Si i = componente no clave j = componente de referencia r (HK) di dr N min i , r m bi br Como fi = di + bi fi bi dr N min 1 i , r m br dr N min f i i , r m br di dr N min 1 i , r m br Rmin, Net infinitas, Zonas de composición cte. Punto de contacto o punto de infinitud Se presenta en sistemas binarios ideales Rmin, Net infinitas, Zonas de composición cte. Punto de contacto o punto de infinitud Se presenta en sistemas binarios no ideales Rmin, Net infinitas, Zonas de composición cte. Sistemas multicomponente Clase I: Tienen 1 punto de infinitud. Todos los componentes se distribuyen. Estrecho punto de ebullición entre LK y HK. Clase II: Tienen 2 puntos de infinitud. Uno o más de los componentes solo aparece en D o en B No todos se distribuyen. Hay 2 ptos. de infinitud lejos de la alimentación Hacia D sí se distribuyen, pero hacia B no. Clase I: Forma general BM desde el punto de infinitud hasta D V yi , L x i , Dx i ,D V L D yi , K i , x i , Sustituyendo K i , xi ,V L x i , Dx i ,D Clase I: Forma general Multiplicando por Para j K j , x j ,V L x j , Dx j ,D V L x i , K i , xi , Dx i ,D K i , x i , Dx i ,D L K i , K i , x i , y V L x j , K j , x j , Dx j ,D K j , x j , Dx j ,D L K j , K j , x j , Dx j ,D Dxi ,D L L K i , K i , x i , K j , K j , x j , L i , j , Dxi ,D i , j , xi , K j , L Dx j ,D x j , xi ,D x j ,D i , j , x j , L xi , D i , j , 1 Clase I: Forma general Para separaciones Clase I las composiciones de la zona de contacto son idénticas a las del equilibrio de flash de la alimentación xi , xLK ,F y x j , x HK ,F Ec. de Underwood para clase I: x i ,D x j ,D i , j , x j , L x i , D i , j , 1 (L )min F LF F xLK ,D x HK ,D LK ,HK ,F x HK ,F L xLK ,F D LK ,HK ,F 1 Dx LK ,D Dx HK ,D LK ,HK ,F LF x HK ,F LF x LK ,F LK ,HK ,F 1 Distribución de componentes no clave Dxi ,D LF x i , F 0 i ,HK ,F 1 DxLK ,D LK ,HK ,F i ,HK ,F Dx HK ,D 1 L x 1 L x LK ,HK ,F LK ,HK ,F F LK ,F F HK ,F Dxi ,D LF x i , F 1 Para Clase I Balance de Energía sobre la zona de rectificación. Reflujo externo (L min )EXTERNO D ( Rmin )EXTERNO Si V y L son constantes, ( Rmin )EXTERNO (L )min D (L )min ( HV H L ) D( HV HV ) D( H V H L ) Clase II: Forma general x i ,D x j ,D i , j , x x L i , j , D i , j , 1 i ,r , zi ,F 1 q i ,r , Problema: Valores de x i , i , j , i ,HK ,F zi ,F 1q i , HK ,F i ,HK ,F xi ,D 1 Rmin i , HK , F Correlación de Gilliland • El número de etapas influye en el costo del sistema de separación. El reflujo influye en los costos de operación de la columna. • Un menor reflujo es necesitado a mayor número de etapas. • La correlación de Gilliland provee una aproximación entre el número de etapas y la razón de reflujo utilizada. Correlación de Gilliland Debe de existir una relación entre el número de etapas teóricas con el número de etapas mínimas y la razón de reflujo. 𝑌= 𝑁 − 𝑁𝑚𝑖𝑛 = 1 − exp 𝑁+1 1 + 54.4𝑋 11 + 117.2𝑋 𝑋−1 𝑋 0.5 Localización del plato de alimentación • Una buena aproximación para la localización del plato de alimentación se obtiene usando la ecuación empírica de Kirkbride: 𝑁𝑅 = 𝑁𝑆 𝑧𝐻𝐾,𝐹 𝑧𝐿𝐾,𝐹 𝑥𝐿𝐾,𝐵 𝑥𝐻𝐾,𝐷 2 𝐵 𝐷 0.206 • En la práctica, las columnas están equipadas con varias etapas de alimentación. Ejemplo 1 La siguiente mezcla de alimentación ha de separarse por destilación ordinaria a 120 psia y 175.7 °F de forma que se obtenga un destilado con 92.5% de lo que se alimenta de nC4 y unas colas de 82 % de iC5 a) Estime el número mínimo de etapas de equilibrio C3 5 que se requieren aplicando la ecuación de Fenske. iC4 15 nC4 25 b) Utilice la ecuación de Fenske para determinar la iC5 20 distribución de los componentes no clave entre el nC5 35 destilado y las colas. c) Utilice el método de Underwood para estimar Rmin. d) Determine el número de etapas teóricas que se requieren, utilizando la correlación de Guilliland suponiendo Rop = 1.2Rmin, un ebullidor parcial y un condensador total. e) Estime la localización de la etapa de alimentación. QD y QB Componente lbmol/h f) Repita todos los cálculos considerando que la columna opera a 80 psia. Distribución inicial destilado con 92.5% de lo que se alimenta de nC4 y unas colas de 82 % de iC5 Componente lbmol/h D Componente lbmol/h C3 iC4 nC4 iC5 nC5 F C3 iC4 nC4 iC5 nC5 5 15 23.125 20 0 COLUMNA 5 15 25 LK 20 HK 35 Componente lbmol/h B C3 iC4 nC4 iC5 nC5 0 0 1.875 16.4 35 Ejemplo 2 Pcol = 80 psia Alimentación en su punto de burbuja a 160 psia Calcular: a) Nmin y Rmin. b) Netapas si Rop = 1.25 Rmin. c) Localización de etapa de alimentación. d) Servicios de condensador y ebullidor. RESUMEN individual: Parte 1: Métodos de grupo (Kremser), pag. 501-525. Agregar un ejemplo resuelto en MathCad Parte 2: Métodos de grupo de Edminster, pag. 525-536. Agregar un ejemplo resuelto en MathCad