Hallar un vector tangente unitario a la curva

Anuncio

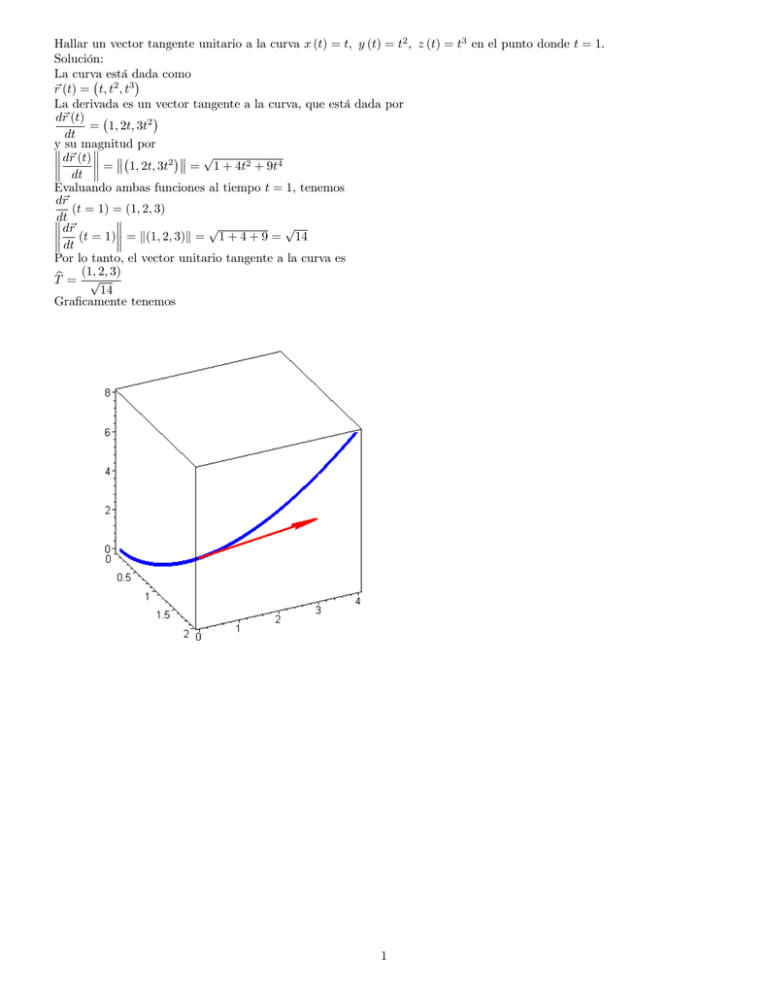
Hallar un vector tangente unitario a la curva x (t) = t; y (t) = t2 ; z (t) = t3 en el punto donde t = 1.
Solución:
La curva está dada como
~r (t) = t; t2 ; t3
La derivada es un vector tangente a la curva, que está dada por
d~r (t)
= 1; 2t; 3t2
dt
y su magnitud por
p
d~r (t)
= 1; 2t; 3t2 = 1 + 4t2 + 9t4
dt
Evaluando ambas funciones al tiempo t = 1, tenemos
d~r
(t = 1) = (1; 2; 3)
dt
p
p
d~r
(t = 1) = k(1; 2; 3)k = 1 + 4 + 9 = 14
dt
Por lo tanto, el vector unitario tangente a la curva es
(1; 2; 3)
Tb = p
14
Gra…camente tenemos
1