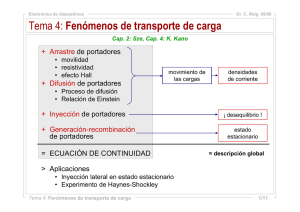
Movimiento térmico de portadores
Anuncio

Transporte de portadores Corriente en los semiconductores Movimiento térmico de los portadores Dentro del semiconductor los portadores de corriente están sometidos a un movimiento de agitación térmica (movimiento browniano). Se trata de un movimiento aleatorio, ya que no hay ninguna dirección preferente. Un portador se mueve en una dirección, colisiona con un átomo u otro portador, se frena o cambia de dirección, sufre el impacto de un portador que lo acelera, etc. Conceptos fundamentales El tiempo promedio entre colisiones se llama τc[s] y varía entre 1014 y 10-13 s a 300K. Entre colisión y colisión los portadores adquieren una velocidad térmica: vth [cm/s]. Aproximadamente es 107 [cm/s] ¡LOS PORTADORES NO VAN A NINGÚN LADO! La longitud característica del movimiento térmico se denomina: Camino libre medio y se denota λ [cm] λ varía entre 1 y 10 nm. Arrastre de portadores Si aplicamos un campo eléctrico sobre un semiconductor se produce un movimiento ordenado de portadores en dirección del campo. Veamos: Ε= Campo eléctrico [V/cm] Sabemos que : F=qE Operando tendremos: F m.a; a dv Portadores: Electrones qE v t cm / s me dv dt F dt m Portadores: huecos v qE t cm / s mh La velocidad varía permanentemente pero se puede obtener una promedio: Velocidad neta en dirección del campo La velocidad promedio de los portadores es la línea punteada en el gráfico La velocidad media se puede asumir como: qE v c cm / s 2mh,e O se puede escribir como: q c v E cm / s 2mh,e A esta velocidad provocada por el campo se le llama velocidad de arrastre y a la constante que los relaciona se le llama movilidad μ: Portadores: Electrones q c n 2me cm 2 V . s cm vn,arrastre n E s Portadores: huecos q c p 2mh cm 2 V . s cm v p ,arrastre p E s Densidad de Corriente de arrastre Analizando las anteriores ecuaciones se pueden obtener algunas conclusiones rápidas: Si τc es grande la movilidad μ será grande también. Si la masa m es pequeña, la movilidad μ será grande. La movilidad también depende del dopaje como se muestra en el siguiente gráfico: Movilidad en función del dopaje Para un bajo nivel de dopaje, es limitada por colisiones con la red Para medio o alto nivel de dopaje, es limitada por colisiones con los dopantes Los huecos son mas "pesados" que los electrones: para el mismo nivel de dopaje, n > p Densidad de corriente de arrastre Jarrastre α velocidad de arrastre Jarrastre α concentración de portadores Jarrastre α carga de los portadores J n,arrastre qnVarrastre qnn E J p,arrastre qpVarrastre qp p E J total,arrastre q(nn p p ) E Densidad de corriente de arrastre La constante que relaciona la densidad de corriente con el campo no es otra que la conductividad σ o su inversa ρ, la resistividad. q(nn p p ) cm 1 1 cm q(n n p p ) Entonces podemos escribir la relación: J E E J Que es la ley de Ohm. Que es la ley de Ohm. En un semiconductor tipo n: En un semiconductor tipo p: 1 cm n qN D n 1 cm p qN A p La relación entre el dopado y la resistividad es como se muestra en el siguiente gráfico (para el silicio a 300K): Siguiendo con el tratamiento de la relación, vemos que: dV J nq dx • Ya que como sabemos: dV E dx Por tanto las relaciones las podemos escribir como: dV J e ni qe dx dV J h ni q h dx dV J J e J h ni q( e h ) dx Se establece una corriente de portadores por causa del gradiente de potencial. Densidad de Corriente de difusión Evidentemente, la agitación térmica no da lugar a ninguna corriente puesto que no hay ninguna dirección privilegiada. Dada una sección del semiconductor, el número de electrones que la atravesarán en un sentido será el mismo, en promedio, que los que la atravesarán en sentido contrario. Este movimiento de agitación térmica da origen a una corriente, llamada corriente de difusión, que se produce cuando hay diferencias en la concentración de un portador en el volumen del semiconductor. En este caso, ocurre un flujo de portadores en el interior del semiconductor que va en el sentido de tender a igualar la concentración. Como los portadores tienen carga, su movimiento origina una corriente. Elementos de la difusión: •Un medio material (Cristal de Si). •Un gradiente de partículas (huecos y electrones) • Dentro del medio las colisiones entre las partículas y el medio dispersan a las partículas en direcciones aleatorias: sin embargo, el movimiento neto de las partículas es en dirección contraria al gradiente Como dijimos, el movimiento neto de las partículas es en dirección contraria al gradiente. El flujo de partículas es, por tanto, directamente proporcional a la derivada de la concentración y de signo contrario. Flujo de difusión α gradiente de concentración # de partículas Flujo cm 2 s n Dn dn dx dp p Dp dx donde D es el coeficiente de difusión característico de cada tipo de proceso. El signo menos en la expresión anterior se añade para indicar que el movimiento de las partículas se producirá desde donde hay más concentración hasta donde hay menos, es decir, en el sentido decreciente de la concentración. Densidad de corriente de difusión Se entiende que Dn y Dp son los coeficientes de difusión para e− y h+ respectivamente. cm 2 D s D mide la facilidad con la que se difunden los portadores en respuesta a un gradiente de concentración: La densidad de corriente de difusión para electrones y huecos se obtendrá simplemente multiplicando la carga por el flujo de difusión de partículas, por lo que: J n,difusión qDn dn A dx cm 2 J p ,difusión qD p dn A dx cm 2 Densidad de Corriente Total El resultado completo de las corrientes es obviamente la suma de ambas, de difusión y de arrastre: dp J p J p ,arrastre J p ,difusión qp p E qD p dx J n J n ,arrastre J n,difusión qn nE qDn dp dx J Total J p J n Como la relación se encuentra en equilibrio la suma de las corrientes será cero. Relación de Einstein: Existe una relación entre los coeficientes de difusión y movilidad, que se conoce como relación de Einstein, que establece la siguiente relación: Dn K BT n q Dp K BT p q Semiconductores extrínsecos El semiconductor extrínseco sea tipo P o N tienen una concentración de cargas libres mucho mayor. Un material de Si tipo N tiene ND=1017 carga/cm3. ND representa también la concentración de electrones libres debidos a las impurezas. Como se puede ver las impurezas en un semiconductor drogado son en cantidades mínimas. El equilibrio térmico se consigue con n.p = ni2 que es la llamada ley de acción de masas. Unión PN La unión PN está conformada por material semiconductor tipo P, por un lado, y material tipo N, por el otro como muestra la figura: P N En la zona de la unión algunos huecos la atraviesan y se recombinan con los electrones de la zona de tipo P. En forma paralela, algunos electrones de la zona de tipo N atraviesan la unión y se recombinan con los huecos de la zona de tipo P.