TRANSICIÓN DE PERCOLACIÓN EN FLUJO EN ROCAS Y
Anuncio

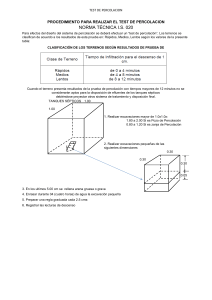
TRANSICIÓN DE PERCOLACIÓN EN FLUJO EN ROCAS Y EXPONENTES ANÓMALOS SULLY GÓMEZ ISIDRO UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN FACULTAD DE MINAS POSGRADO EN APROVECHAMIENTO DE RECURSO HIDRÁULICOS 2000 TRANSICIÓN DE PERCOLACIÓN EN FLUJO EN ROCAS Y EXPONENTES ANÓMALOS SULLY GÓMEZ ISIDRO IC, M. Sc. Tesis para optar el título de doctor en ingeniería En aprovechamiento de recursos hidráulicos. Director OSCAR MESA SÁNCHEZ IC, PhD. UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN FACULTAD DE MINAS POSGRADO EN APROVECHAMIENTO DE RECURSO HIDRÁULICOS 2000 ii iii iv v A mi familia, a mis amigos, a mi país adolorido. vi AGRADECIMIENTOS Expreso mis más sentidos agradecimientos a Doctor Oscar José Mesa Sánchez, Director de esta Tesis, por sus oportunas y sabias orientaciones y por su gran confianza en mi. Posgrado en Aprovechamiento de Recursos Hidráulicos, profesores, estudiantes y trabajadores, quienes con su calidad técnica y humana apoyaron siempre el desarrollo de esta investigación. Universidad Industrial de Santander, que me brindó su apoyo material y pedagógico para la realización de la Tesis. Colciencias, por su apoyo económico en el inicio, desarrollo y culminación del doctorado; por su apoyo se hace posible la investigación en este país. Diana Ospina, por su valiosa e incansable ayuda en la búsqueda bibliográfica y su apoyo personal. Angela María de Jesús Bustamante, por el apoyo logístico y espiritual que me brindó durante este proceso. vii La tierra que no es labrada llevará abrojos y espinas aunque sea fértil, así el entendimiento humano. Santa Teresa de Jesús viii CONTENIDO pág. 1. INTRODUCCION 1 2. REVISION DE LITERATURA 4 2.1 El flujo en fracturas simples 4 2.2 Sistemas de fracturas 6 2.3 Conectividad de fracturas 9 2.4 Teoría de percolación en sistemas de fracturas. 10 2.5 Pruebas hidráulicas 12 3. FUNDAMENTOS DE FLUJO EN ROCAS 14 3.1 Conceptos fundamentales de flujo 15 3.2 Planteamiento del problema del flujo en medios fracturados 18 3.2.1 Condiciones de flujo en la escala de la fractura 18 3.2.2 Condiciones de flujo en la escala de sistemas de fracturas 19 3.2.3 Ecuaciones de flujo en rocas 21 3.2.3.1 Analogía ente el flujo de calor en materiales y el flujo en acuíferos 24 3.2.3.2 Solución analítica a la ecuación de calor 25 3.3 Planteamiento matemático para flujo en medio poroso fracturado 26 3.4 Grupos de renormalización, funciones homogéneas y exponentes anómalos 28 3.4.1 Autosemejanza, escalamiento y homogeneidad. 29 3.4.2 Grupos de renormalización 30 ix 3.4.2.1 Grupos de renormalización de Lie 31 3.4.2.2 Conceptos básicos 32 3.4.2.3 Aplicación de los Grupos de Lie a la ecuación de difusión 34 3.4.2.4 Solución de la ecuación de flujo en medio poroso a partir de Grupos de Lie 36 3.5 Análisis dimensional y soluciones asintóticas 38 3.6 Leyes de conservación de masa 42 3.7. No-linealidad del flujo en yacimientos y acuíferos 44 3.7.1 Flujo en medios elásticos 44 3.7.2 Flujo en medios elastoplásticos. 45 3.7.2.1 Variaciones de presión a partir de perturbaciones en los yacimientos 46 3.7.2.2 Proceso de caída de presión 46 3.7.2.3 Proceso de aumento de presión 47 3.7.3 Coeficiente de difusividad en acuíferos 47 3.7.4 Leyes de autosemejanza en el flujo en pozos 48 3.7.4.1 Ley de autosemejanza de primer orden 48 3.7.4.2 Ley de similaridad de segundo orden 50 3.7.5 El problema con coeficiente discontinuo en pruebas de pozos 51 3.7.5.1 Bombeo periódico en pozos 52 3.7.5.2 Ley de autosemejanza de segundo orden 54 3.7.6 Recuperación de niveles 55 3.8 Teoría de percolación y el flujo en rocas 56 3.8.1 El flujo en rocas como una transición de percolación 57 3.8.2 Transición de fase y umbrales de percolación 59 3.8.2.1 Transición de percolación 61 3.8.2.2 Leyes de escalamiento en sistemas de tamaño finito 63 3.8.2.3 Probabilidad de percolación y escalamiento 65 3.8.2.4 Umbrales de percolación en mallas de tamaño finito. 67 3.8.3 Caracterización de racimos de fracturas 68 3.8.4 Estructura del racimo principal 69 3.8.5 Escalamiento de parámetros de flujo desde la teoría de percolación 71 x 4. EXPERIMENTOS NUMÉRICOS EN ACUÍFEROS FRACTURADOS 74 4.1 Estimación de umbrales de percolación 75 4.1.1 Simulaciones Montecarlo 75 4.1.2 Probabilidad de percolación y estimación de umbrales 76 4.1.3 Estimación del exponente ν 79 4.1.4 Longitud de correlación para sistemas simulados 80 4.2 Modelo de acuíferos fracturados como sistemas de percolación 82 4.2.1 Modelo de flujo 88 4.2.1.1 Programa de flujo 88 4.2.1.2 Realizaciones de arreglos de fracturas 89 4.2.2 Estimación de parámetros hidráulicos 90 4.3 Discusión y análisis de resultados 94 5. CONCLUSIONES Y RECOMENDACIONES 105 REFERENCIAS 112 xi LISTA DE FIGURAS pág Figura 3.1 Esquema explicativo del VER. Bear (1972). 16 Figura 3.2 Esquema de flujo en planos de fracturas continua. 17 Figura 3.3 Esquema de canales de flujo en el plano de la fractura. 19 Figura 3.4 Esquema de intersección de planos de fracturas. 20 Figura 3.5 Oscilación de presión de bombeo periódico 53 Figura 3.6 Esquema de una malla de percolación por sitios 62 Figura 3.7 Esquema de comportamiento de la densidad de sitios 64 Figura 3.8 Esquema de variación de probabilidad de percolación 65 Figura 3.9 Sección Vertical de un campo de pozos 68 Figura 3.10 Ejemplo de patrones que simulan fracturas aleatorias 70 Figura 3.11 Conductividad y Resistencia en sistemas de percolación 72 Figura 4.1 Umbrales de percolación en mallas de tamaño finito 77 Figura 4.2 Variación del umbral de percolación en función de L 78 Figura 4.3 Efecto de tamaño finito en el umbral de percolación 79 Figura 4.4 Estimación del exponente ν 80 Figura 4.5 Comportamiento de la longitud de correlación 81 Figura 4.6 Mallas radiales de percolación 84 Figura 4.7.1 Sistema de fracturas sobre el umbral de percolación. 85 Figura 4.7.2 Racimo principal en malla 128 con densidad 0.6 86 Figura 4.7.3 Localización de pozos de observación. 87 Figura 4.8 Ajuste de curvas de abatimiento en simulaciones numéricas, Pozo de observación 1 y 2 Figura 4.9 92 Ajuste de curvas de abatimiento en simulaciones numéricas, Pozo de observación 3 y 4 93 xii Figura 4.10 Variación de difusividad y conductividad hidráulica. Efecto de escala. Figura 4.11 95 Conductividad hidráulica y efecto de cercanía al umbral de percolación . Figura 4.12 96 Parámetros hidráulicos en función de cercanía al umbral de percolación. 97 Figura 4.13 Parámetros hidráulicos en función del tamaño del sistema 100 Figura 4.14 Parámetros hidráulicos en función de la resolución del sistema 102 Figura 4.15 Comportamiento transitorio de la cabeza hidráulica en acuíferos 104 xiii LISTA DE TABLAS pág. Tabla 1. Umbrales de percolación estimados para mallas cilíndricas 77 Tabla 2. Valores de Δ para mallas de tamaño finito 79 Tabla 3. Leyes de escalamiento de los parámetros hidráulicos 82 Tabla 4. Resultados de simulaciones en malla 128 98 Tabla 5. Resultados de simulaciones en malla 256 98 Tabla 6. Exponentes de la ley de escalamiento. Resolución 3.9. 100 Tabla 7. Exponentes de la ley de escalamiento. Resolución 1. 101 xiv RESUMEN El objetivo de este trabajo es ofrecer un mayor conocimiento sobre la física del fenómeno del flujo en sistemas de fracturas en rocas bajo los efectos de pruebas hidráulicas. Se presentan lineamientos importantes para el estudio del flujo en sistemas geológicos que tienen un alto grado de heterogeneidad, entre ellos, la interpretación y manejo de estos medios como el producto de una transición de fase. Para obtener las leyes de escalamiento de los parámetros hidráulicos que rigen el flujo en esta aproximación y considerar el efecto de las escalas en el fenómeno, se diseñan experimentos numéricos que representan sistemas de fracturas en estado de transición y se encuentran sobre un umbral de flujo. Para simular pruebas hidráulicas sobre estos sistemas se aplican condiciones de flujo que permiten representar pruebas de bombeo en arreglos radiales de acuíferos fracturados. Las leyes de escalamiento de fenómenos críticos son universales y se expresan en forma de ley de potencia, en este trabajo se obtienen los exponentes críticos de los parámetros que rigen el flujo en sistemas de fracturas. Se expone la teoría de un caso de flujo no lineal en pozos y se plantea un problema de bombeo que da lugar a la consideración de una nueva escala. Se espera proyectar estas teorías en la interpretación y manejo de pruebas hidráulica de campo, así como también resaltar escalas relevantes del fenómeno y sus exponentes anómalos, no consideradas en los enfoques clásicos de solución. xv ABSTRACT This work aims at understanding the flow phenomena in fracture systems under hydraulic test effects. Important features are presented for studying flow in geologic media that have high degree of heterogeneity. The most important feature is the consideration of the fractured medium as a phase transition. To obtain scaling laws of hydraulic parameters near the thresholds and to consider the scale effect numerical experiments are designed to represent fracture systems in percolation transition. In order to simulate hydraulic tests on these systems flow conditions are imposed in form of pumping tests in fractured aquifers using radial percolation arrays. Universality in critical phenomena permits us to express hydraulic parameters in form of power laws. In this work critical exponents in fracture systems are obtained. Besides, dimensional analysis and renormalization group in the flow theory are briefly presented in a special case of nonlinear flow in pumping well. In that case we have to consider a new scale, the well radio. We hope to project the above theories toward the interpretation and handling of field hydraulic tests and to present important scales and their anomalous exponents in the study of rock flow phenomena, not considered in classical theories of solution. xvi xvii