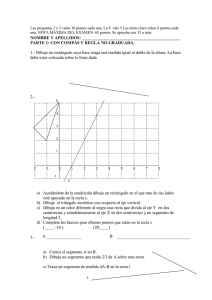
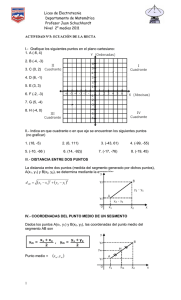
ejercicios de geometría (1º y 3º eso)
Anuncio

GEOMETRÍA BÁSICA. 2013-2014. PERPENDICULARIDAD: Existe perpendicularidad entre dos elementos cuando estos se cortan formando un ángulo de 90º 1º Caso de perpendicularidad. (MEDIATRIZ). A) Partimos de un segmento AB. B) Hacemos centro en A y en B, con una medida mayor que la mitad del segmento, y dibujamos 2 arcos. C) Los dos arcos se cortan en los puntos C y D. D) Al unirlos dibujamos la mediatriz del segmento, obteniendo el punto M. Definición de mediatriz: perpendicular que corta al segmento en dos partes iguales. 2º Caso. A) Partimos de una recta r y un punto P exterior a ella. B) Con centro en P y una medida mayor que la distancia de P a la recta dibujamos un arco que la corte en dos puntos. A y B. C) Seguidamente operamos como en el caso anterior, haciendo la mediatriz. D) Obteniendo la perpendicular que pasa por P. 3º Caso. A) Partimos de una recta r y un punto P exterior a ella. B) Tomamos dos puntos cualesquiera en la recta A y B. C) Haciendo centro en A y en B con distancia hasta P, dibujamos dos arcos que se cortaran en el punto C. D) Unimos P con C y obtenemos la perpendicular pedida. 4º Caso. A) Partimos de una recta y un punto P en ella. B) Con centro en P y una medida cualquiera hacemos una semicircunferencia que corte a la recta en dos puntos A y B. C) Procediendo a continuación como la mediatriz, dándonos el punto C. D) Unimos C con P y hemos dibujado la perpendicular. 5º Caso. (MÉTODO DE LOS 4 ARCOS). A) Partimos de una semirrecta. B) Con centro en A y con una medida cualquiera dibujamos un arco que corte a la semirrecta en B. C) Con centro en B y con igual radio dibujamos un arco que se corte con el anterior en C. D) Centro en C y realizamos la misma operación para obtener D. E) Repetimos lo mismo con centro en D y obtenemos E. F) Unimos A con E, para dibujar la perpendicular por A. PARALELISMO: El paralelismo se produce entre rectas cuyos puntos sean equidistantes. 1º Caso. A) Partimos de una recta r y un punto exterior P. B) Haciendo centro en P, con una medida mayor que la distancia de P a la recta trazamos un arco que corte a la misma en A. C) Con centro en A e igual radio hacemos otro arco que pase por P y corte a la recta en B. D) Se toma la distancia de B a P, y se traslada a partir de A, de modo que el arco se corta en C. E) Unimos C con P y ya hemos dibujado la paralela. 2º Caso. A) Partimos de una recta r y nos mandan dibujar otra a una distancia concreta. B) Tomamos dos puntos cualesquiera en la recta A y B. C) Aplicamos el caso nº 4 de perpendicularidad en cada uno de ellos. D) Teniendo las perpendiculares medimos sobre ellas la distancia concreta, dándonos dos puntos. E) Unimos los dos puntos y podemos dibujar la paralela. 3º Caso. A) Partimos de la recta y un punto exterior P. B) Tomamos un punto cualquiera en la recta A. C) Haciendo centro en A y con radio hasta P, dibujamos una semicircunferencia que corte a la recta en B y C. D) Se toma la distancia de B a P y se lleva a partir de C, obteniendo D. E) Se une P con D y podemos dibujar la recta pedida. BISECTRIZ: es la semirrecta que divide a un ángulo en dos partes iguales. 1º Caso. A) Partimos de un ángulo Â. B) Haciendo centro en A con una medida cualquiera dibujamos un arco que cortará en dos puntos B y C a las semirrectas lado. C) Con igual medida se hace centro en B y en C y se dibujan dos arcos que se cortaran en D. D) Se une D con A y ya se determina la bisectriz. 2º Caso. A) Partimos del ángulo Â. B) Con centro en A se dibujan dos arcos de diferente radio. C) Obteniéndose los puntos B, C, D y E. D) Ahora se unen de forma cruzada, y se origina el punto F. E) Se une A con F y se consigue la bisectriz. ÁNGULO: El ángulo es la superficie comprendida entre dos semirrectas de inicio común. Se mide en grados minutos y segundos. 1º Caso. (SUMA DE ÁNGULOS). A) Partimos de dos ángulos el  y el B. B) Sobre una de las semirrectas lado de uno de los ángulos trasladamos la abertura del otro, hacía fuera. C) Obteniendo así la suma de ambos. 2º Caso. (RESTA DE ÁNGULOS). A) Partimos de dos ángulos el  y el B. B) Sobre una de las semirrectas lado del ángulo mayor trasladamos la abertura del otro ángulo hacía dentro. C) Obteniendo así la diferencia entre ambos. TRAZADO DE ÁNGULOS CON COMPÁS. Este trazado se fundamenta en la utilización de los ángulos y sus posibles combinaciones, además de la operatividad de sus bisectrices. POLÍGONOS: Los polígonos son superficies bidimensionales, acotadas. El polígono básico es el triángulo. ELEMENTOS DE UN POLÍGONO: Lados: son los segmentos que acotan la superficie. Vértices: son los puntos de corte de los lados de un polígono. Ángulos: son los grados comprendidos entre dos lados de un polígono. TRIÁNGULOS Alturas: son las perpendiculares a los lados desde el vértice opuesto. Pie de la altura: es el punto donde se produce la perpendicularidad. Ortocentro: punto de corte de las tres alturas. Triángulo órtico: es el triángulo que tiene como vértices los pies de las alturas. Mediatrices: son las perpendiculares que dividen a los lados en dos partes iguales. Circuncentro: es el punto de corte de las tres mediatrices del triángulo: Circunferencia circunscrita: es la circunferencia de centro el circuncentro y que pasa por los tres vértices del triángulo. Medianas: son los segmentos que unen el punto medio del lado con el vértice opuesto. Baricentro: es el punto de corte de las tres medianas del triángulo. Triángulo complementario: es el que tiene por vértices los puntos medios de los lados del triángulo. Bisectriz: es la semirrecta que divide al ángulo en dos partes iguales. Incentro: es el punto de corte de las tres bisectrices del triángulo. Circunferencia inscrita: es la circunferencia tangente interior al triángulo, cuyo centro es el incentro. CONSTRUCCIÓN DE POLÍGONOS: TRIÁNGULO CONOCIENDO EL LADO. A) Partimos del segmento AB. B) Haciendo centro en A y centro en B con la medida del lado, se trazan dos arcos que se cortaran en el punto C. C) Se une C con cada uno de los extremos del segmento y ya está dibujado el triángulo. TRIÁNGULO CONOCIENDO EL RADIO. A) Se parte de dos rectas perpendiculares que se cortan en O. B) Con centro en O se dibuja una circunferencia de radio dado. Obteniéndose los puntos A, B, C, y D. C) Con centro en C y medida igual a la del radio se dibuja una semicircunferencia que pasa por O, dándonos los puntos de corte E y F. D) Dichos puntos se unen con A, y se consigue el triángulo. CUADRADO CONOCIENDO EL LADO. A) Se parte del segmento AB. B) Por el extremo A se dibuja una perpendicular repasando el trazado de los cuatro arcos. C) Se toma la medida del lado y se hace centro en A dibujando un arco que corte a la perpendicular en G. D) Con centro en G e igual medida de dibuja otro arco en sentido hacía arriba. E) Con centro en B e igual medida hacemos otro arco que se corte con el anterior en H. Cuarto vértice del pentágono. F) Se unen los puntos A, B, G y H. CUADRADO CONOCIENDO EL RADIO. A) Partimos de las dos rectas perpendiculares que se cortan en O. B) Con centro en O y radio dado, se dibuja una circunferencia que se cortará en los puntos A, B, C y D. C) Sí se unen estos cuatro puntos se obtiene un cuadrado inscrito en la circunferencia. D) Pero si se dibujan las paralelas a los diámetros por los puntos anteriores obtenemos otros cuatro: E, F, G, y H. Que son vértices del cuadrado circunscrito. PENTÁGONO CONOCIENDO EL LADO. A) Partimos del segmento AB. B) Dibujamos la mediatriz del segmento y dibujamos una paralela a ella por el extremo B. C) Con centro en B y con medida AB dibujamos un arco que se corte con la paralela a la mediatriz en C. D) Con centro en M hasta C, trazamos un arco que se corte con la prolongación del segmento en D. E) Desde A hasta D, dibujamos un arco que se cortará con la mediatriz en E. F) Desde E y con medida AB se traza una semicircunferencia hacía abajo. Ésta se cortará con los arcos desde A y desde B, con la medida AB. G) Obteniéndose los puntos F y G, vértices del pentágono. PENTÁGONO CONOCIENDO EL RADIO. A) Se parte de las dos rectas perpendiculares que se cortan en O. B) Con centro en O y radio dado se dibuja la circunferencia dándonos los puntos A, B, C y D. C) Con centro en D y radio el de la circunferencia se dibuja una semicircunferencia que cortará a la circunferencia en los puntos E y F. D) Se unen E y F, encontrando el punto M en el radio DO. E) Desde M hasta A se dibuja un arco que corte al radio CO en el punto G. F) Desde A hasta G se dibuja otro arco en sentido ascendente, que corte a la circunferencia en H. G) El segmento AH es el lado del pentágono buscado. HEXÁGONO CONOCIENDO EL LADO. A) Se parte del segmento AB. B) Con centro en A y en B con la medida del lado se dibujan dos arcos que se cortaran en O. C) Con centro en O y radio hasta A se dibuja una circunferencia sobre la cual llevaremos cinco veces más la medida del segmento. HEXÁGONO CONOCIENDO EL RADIO. A) Se parte de las dos rectas perpendiculares que se cortan en el punto O. B) Con centro en O y radio dado se hace una circunferencia obteniéndose los puntos A, B, C y D. C) Con centro en A y en B con la medida del radio se dibujan dos semicircunferencias que pasen por O, teniéndose los puntos: E, F, G y H. D) A se une con E y F; mientras que B se une con G y H. Después se une E con G y F con H. Consiguiéndose el hexágono.