Campo
Anuncio

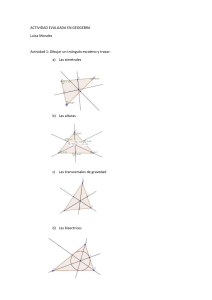
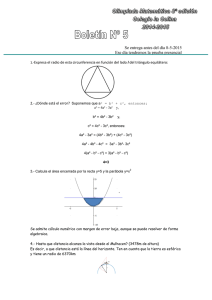
Problema 271 Sean un triángulo isósceles, con ; su ortocentro y su triángulo órtico. Demostrar que es el inverso de respecto de la circunferencia de diámetro . Solución de Saturnino Campo Ruiz, Profesor de Matemáticas jubilado, de Salamanca. Sea el centro de esa circunferencia. Para que rencia se ha de verificar sea el inverso de respecto de esa circunfe- (*). Sea es el simétrico de respecto del lado ; como sabemos, está en la circunferencia circunscrita al triángulo isósceles , diametralmente opuesto a y por ello el triángulo es rectángulo en . Tenemos pues y según el teorema de la altura, ese producto es igual como queríamos demostrar. al cuadrado de la altura sobre la hipotenusa, o sea, a