T * Cv = f ( T )
Anuncio

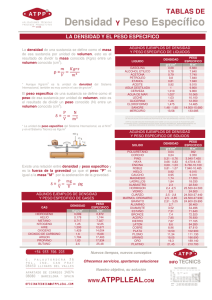
Hoja 1 / 1 TURBOMAQUINAS 67.20 UTILIZACION DE LAS TABLAS DE SCHMIDT Para poder desarrollar en forma adecuada las formulas de la mayor parte de los procesos termodinámicos en los que intervienen gases se ha recurrido a la simplificación de considerar gases ideales con calor especifico constante. Pero esta no es la realidad ya que en la mayor parte de los gases reales los calores específicos aumentan con la temperatura, especialmente a temperaturas elevadas. La razón por la cual se recurre a la idealización de los gases suponiendo que tienen calores específicos constantes es para poder desarrollar las formulas con un grado adecuado de complejidad. Si fuera necesario desarrollar la teoría teniendo en cuenta que los calores específicos no son constantes, la complejidad de las formulas seria tal que seria imposible desarrollar dicha teoría. Las tablas de SCHMIDT han sido preparadas para cálculos termodinámicos a volumen constante, tales como los que se desarrollan en los motores de combustión interna. En las turbinas a gas el proceso de combustión se desarrolla a presión constante y la utilización de las tablas de Schmidt no es directo. Las tablas de Schmidt presentan el valor medio del producto M*Cv ( Peso molecular por el calor especifico a volumen constante ) entre 0 y T ºK ( columnas 2 y 6 ) en función de la temperatura en ºK ( columnas 1 y 5 ). Nosotros necesitamos el valor medio de Cp ( calor especifico a presión constante ) entre temperaturas definidas Ti y Tj ( ambas distintas de cero ). Recordemos que donde Cp = Cv + R / M (1) Cp = Calor especifico a presión constante Cv = Calor especifico a volumen constante R = Constante universal para los gases = 8.3143 J / Mol * ºK M = Peso molar del gas en Kg / Mol La formula anterior vale tanto para los gases reales como para los gases ideales ya que su deducción fue hecha sobre bases termodinámicas sin limitaciones. Para obtener el valor medio del calor especifico a presión constante, podemos construimos una gráfica de la función T T * Cv 0 = ( gráfica en la próxima hoja ) f(T) (2) Hoja 2 / 2 T * Cv T 0 T * Cv Tj 0 Pendiente = Cv Pendiente = Cv Pendiente = Cv Ti 0 Ti Tj = Tj * Cv 0 Tj Ti T Tj Del gráfico anterior surge que el valor buscado de rectas, y esta dado por: Tj Cv Ti T 0 Cv Tj Ti es la pendiente de una de las Ti - Ti * Cv 0 (3) Tj - Ti De esta expresión podemos pasar a: Tj Tj Cp Ti = Cv Ti + R / M (4) que será el valor del calor especifico a presión constante medio entre las temperaturas Ti y Tj, que necesitamos utilizar entre dichas temperaturas.