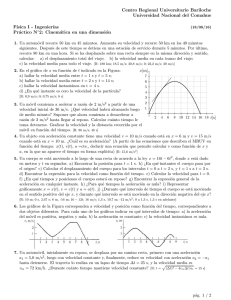
5/4 Sustituyendo la x por el valor dado, 22-3=2-1 ==> 2-1=2-1

PARCIAL No 1. CÁLCULO DIFERENCIAL 2016-2
código
Nombre:
Comprender la evaluación es parte de la evaluación. No se resuelven dudas durante el examen. Las tres primeras preguntas son de
selección múltiple y se debe incluir una justificación o porqué de la elección. Las dos últimas son abiertas.
1. Una de las siguientes es falsa, indicar cuál es y porqué
a) la función y = x3 es una función creciente
√
b) el dominio para f (x) = x2 − 25 es
Df = (−∞, −5] U [5, ∞)
√
c) el dominio para la función f (x) = x − 3 es
Df = [3, ∞)
5. Si se lanza una bola directamente hacia arriba con una
velocidad de 40 pies/s, su altura (en pies) después de t
segundos está dada por y = 40t − 16t2 . a)¿Cuál es la
altura máxima que alcanza la bola? b) ¿Para qué valor
de t se presenta la máxima altura?
d) la recta que pasa por los puntos (1, 3) y (5, −2)
tiene pendiente m = − 53
La pendiente vale m=-5/4
a) la altura máxima es 25pies
b) la máxima altura se presenta para t=5/4 segundos
2. Es válido afirmar que
a) f (x) = 3x + 4 es una recta paralela
con g (x) = 4x + 3
b) f (x) =
x2
si x < 0
, es una función par
1 − x si x ≥ 0
c) si f (x) = ex entonces f (ln x) = x2
d) La solución de 22x−3 = 2−1 es x = 1.
Sustituyendo la x por el valor dado,
22-3=2-1 ==> 2-1=2-1
3. Para la función f (x) =
x+1
es válido afirmar que
2 (x − 1)
a) x=1 es una ası́ntota vertical
b) y=1 es una ası́ntota horizontal
c) La gráfica pasa por el origen
d) Corta el eje x en 1
Si x=1 en el denominador resulta un cero...
.
4. El gerente de una fábrica de muebles encontró que cuesta $2 200 fabricar 100 sillas en un dı́a y $4 800 producir
300 sillas en un solo dı́a. a) Exprese el costo en función del número de sillas producidas, suponiendo que es
lineal. b) ¿Cuál es la pendiente de la gráfica y qué representa? c) ¿Cuál es la intersección en y de la gráfica y
qué representa?
a) y=13x+900
b) m=13, representa que
por cada silla el costo sube en $13
c) b=900, significa que aunque no se fabrican sillas
existen unos costos fijos de 900...