Gu´ıa de Problemas Resueltos de F´ısica General.

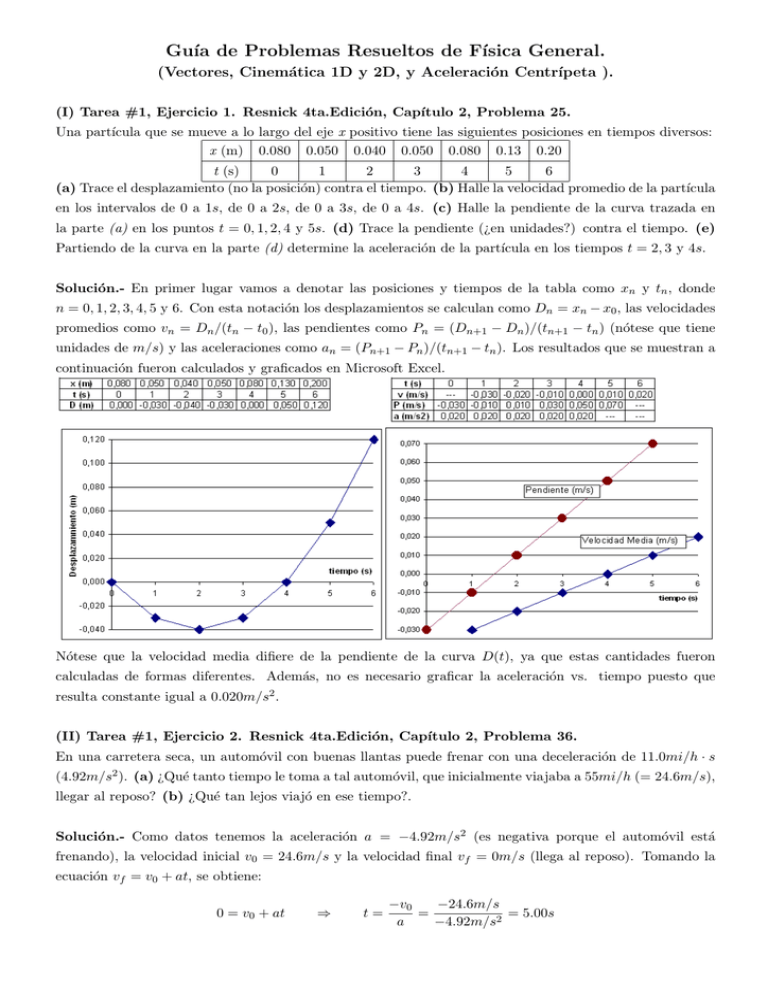
Guı́a de Problemas Resueltos de Fı́sica General.
(Vectores, Cinemática 1D y 2D, y Aceleración Centrı́peta ).
(I) Tarea #1, Ejercicio 1. Resnick 4ta.Edición, Capı́tulo 2, Problema 25.
Una partı́cula que se mueve a lo largo del eje x positivo tiene las siguientes posiciones en tiempos diversos:
x (m) 0.080 0.050 0.040 0.050 0.080 0.13 0.20
t (s)
0
1
2
3
4
5
6
(a) Trace el desplazamiento (no la posición) contra el tiempo. (b) Halle la velocidad promedio de la partı́cula
en los intervalos de 0 a 1s, de 0 a 2s, de 0 a 3s, de 0 a 4s. (c) Halle la pendiente de la curva trazada en
la parte (a) en los puntos t = 0, 1, 2, 4 y 5s. (d) Trace la pendiente (¿en unidades?) contra el tiempo. (e)
Partiendo de la curva en la parte (d) determine la aceleración de la partı́cula en los tiempos t = 2, 3 y 4s.
Solución.- En primer lugar vamos a denotar las posiciones y tiempos de la tabla como xn y tn , donde
n = 0, 1, 2, 3, 4, 5 y 6. Con esta notación los desplazamientos se calculan como Dn = xn − x0 , las velocidades
promedios como vn = Dn /(tn − t0 ), las pendientes como Pn = (Dn+1 − Dn )/(tn+1 − tn ) (nótese que tiene
unidades de m/s) y las aceleraciones como an = (Pn+1 − Pn )/(tn+1 − tn ). Los resultados que se muestran a
continuación fueron calculados y graficados en Microsoft Excel.
Nótese que la velocidad media difiere de la pendiente de la curva D(t), ya que estas cantidades fueron
calculadas de formas diferentes. Además, no es necesario graficar la aceleración vs. tiempo puesto que
resulta constante igual a 0.020m/s2 .
(II) Tarea #1, Ejercicio 2. Resnick 4ta.Edición, Capı́tulo 2, Problema 36.
En una carretera seca, un automóvil con buenas llantas puede frenar con una deceleración de 11.0mi/h · s
(4.92m/s2 ). (a) ¿Qué tanto tiempo le toma a tal automóvil, que inicialmente viajaba a 55mi/h (= 24.6m/s),
llegar al reposo? (b) ¿Qué tan lejos viajó en ese tiempo?.
Solución.- Como datos tenemos la aceleración a = −4.92m/s2 (es negativa porque el automóvil está
frenando), la velocidad inicial v0 = 24.6m/s y la velocidad final vf = 0m/s (llega al reposo). Tomando la
ecuación vf = v0 + at, se obtiene:
0 = v0 + at
⇒
t=
−24.6m/s
−v0
=
= 5.00s
a
−4.92m/s2
Para la parte (b) utilizamos la ecuación vf2 = v02 + 2a(xf − x0 ), y resulta:
0 = v02 + 2a(xf − x0 )
⇒
xf − x0 =
−(24.6m/s)2
−v02
=
= 61.5m
2a
2 × −4.92m/s2
Nótese que se calculó xf − x0 lo que representa el desplazamiento, y además no se utilizó el tiempo calculado
en la parte (a), debido a que en su defecto se utilizó la velocidad final.
(III) Tarea #1, Ejercicio 3. Resnick 4ta.Edición, Capı́tulo 2, Problema 39.
Un tren partió del reposo y se movió con aceleración constante. En un momento dado estaba viajando a
33.0m/s, y 160m más adelante lo estaba haciendo a 54.0m/s. Calcule (a) la aceleración, (b) el tiempo
requerido para recorrer 160m, (c) el tiempo requerido para que alcance una velocidad de 33.0m/s, y (d) la
distancia recorrida desde el reposo hasta el momento en que el tren tuvo una velocidad de 33.0m/s.
Solución.- En este problema se conocen las velocidades en dos puntos de la trayectoria: v1 = 33.0m/s y
v2 = 54.0m/s, donde x2 − x1 = 160m es la distancia entre aquellos dos puntos. Para calcular la aceleración
utilizamos la ecuación vf2 = v02 + 2a(xf − x0 ) con los subı́ndices inicial= 1 y final=2, con lo que queda:
v22 = v12 + 2a(x2 − x1 )
⇒
a=
(54.0m/s)2 − (33.0m/s)2
v22 − v12
=
= 5.71m/s2 .
2(x2 − x1 )
2 × 160m
La parte (b) se refiere al tiempo que paso entre los puntos x1 y x2 , donde el tren recorrió 160m. Para ello
podemos utilizar la ecuación xf = x0 + 12 t(v0 + vf ) con los subı́ndices utilizados anteriormente:
1
x2 = x1 + t(v1 + v2 )
2
⇒
t=
2(x2 − x1 )
2 × 160m
=
= 3.68s.
v2 + v1
54.0m/s + 33.0m/s
Las partes (c) y (d) se refieren al tiempo y al desplazamiento del tren cuando, partiendo del reposo, adquiere
una velocidad final de vf = 33.0m/s. Para calcular el tiempo podemos utilizar la ecuación vf = v0 + at con
v0 = 0m/s:
vf = at
⇒
t=
vf
33.0m/s
=
= 5.78s;
a
5.71m/s2
mientras que para calcular el desplazamiento, podemos recurrir a la ecuación vf2 = v02 + 2a(xf − x0 ):
vf2 = 2a(xf − x0 )
⇒
xf − x0 =
vf2
(33.0m/s)2
=
= 95.4m.
2a
2 × 5.71m/s2
(IV) Tarea #1, Ejercicio 4. Resnick 4ta.Edición, Capı́tulo 2, Problema 58.
Una pelota arrojada hacia arriba tarda 2.25s en llegar a una altura de 36.8m. (a) ¿Cuál fue su velocidad
inicial?, (b) ¿Cuál es su velocidad esta altura?, (c) ¿Cuánta más altura alcanzará la pelota?
Solución.- Para calcular la velocidad inicial podemos utilizar la ecuación y = y0 + vo t + 12 at2 con y0 = 0m
(colocando el origen en el suelo) y a = −g (g = 9.8m/s2 ):
1
y = v0 t − gt2
2
⇒
v0 =
y 1
36.8m 1
+ gt =
+ (9.8m/s2 )(2.25s) = 27.4m/s.
t
2
2.25s
2
La velocidad para esa altura se encuentra utilizando la ecuación v 2 = v02 + 2a(y − y0 ) o con v = v0 + at,
donde v0 es la velocidad inicial calculada en la parte anterior. De la segunda ecuación resulta:
v = v0 − gt = 27.4m/s − (9.8m/s2 )(2.25s) = 5.33m/s.
El hecho de que la velocidad resultó positiva nos indica que para 2.25s la pelota está subiendo. Por otro
lado, la altura máxima se calcula introduciendo la velocidad igual a cero en la ecuación v 2 = v02 + 2a(y − y0 ):
0 = v02 − 2gy
⇒
y=
(27.4m/s)2
v02
=
= 38.3m.
2g
2 × 9.8m/s2
(V) Tarea #1, Ejercicio 5. Resnick 4ta.Edición, Capı́tulo 2, Problema 53.
(a) ¿A qué velocidad debe ser arrojada una pelota verticalmente hacia arriba con objeto de que llegue a
una altura máxima de 53.7m?. (b)¿Cuánto tiempo estuvo en el aire?
Solución.- Al igual que el problema anterior, la altura máxima implica las condiciones v = 0m/s, y0 = 0m
y a = −g en la ecuación v 2 = v02 + 2a(y − y0 ):
0=
v02
− 2gy
⇒
v0 =
p
2gy =
q
2 × 9.8m/s2 × 53.7m = 32.4m/s.
Para este caso, el tiempo de vuelo se calcula imponiendo la condición y = 0m en la ecuación y = y0 +v0 t+ 12 at2 :
1
0 = v0 t − gt2
2
⇒
t=
2v0
2 × 32.4m/s
=
= 6.62s.
g
9.8m/s2
(VI) Tarea #1, Ejercicio 6. Resnick 4ta.Edición, Capı́tulo 3, Problema 19.
Dos vectores están dados por ~a = 4ı̂ − 3̂ + k̂ y ~b = −ı̂ + ̂ + 4k̂. Halle (a) ~a + ~b, (b) ~a − ~b, (c) un vector ~c
tal que ~a − ~b + ~c = 0.
Solución.~a + ~b = (4 + (−1))ı̂ + (−3 + 1)̂ + (1 + 4)k̂ = 3ı̂ − 2̂ + 5k̂.
~a − ~b = (4 − (−1))ı̂ + (−3 − 1)̂ + (1 − 4)k̂ = 5ı̂ − 4̂ − 3k̂.
Si ~a − ~b + ~c = 0, despejamos ~c y queda:
~c = −(~a − ~b) = −(5ı̂ − 4̂ − 3k̂) = −5ı̂ + 4̂ + 3k̂.
(VII) Tarea #1, Ejercicio 7. Resnick 4ta.Edición, Capı́tulo 3, Problema 23.
Dos vectores ~a y ~b tienen magnitudes iguales de 12.7
unidades.
Están orientados como se muestra en la
figura y su vector suma es ~r. Halle (a) las componentes
x y y de ~r, (b) la magnitud de ~r, y (c) el ángulo que
forma ~r con el eje +x.
Solución.El vector ~a en su forma canónica resulta:
~a = 12.7 cos(28.2o )ı̂ + 12.7 sin(28.2o )̂ = 11.19ı̂ + 6.001̂.
Por otro lado, el vector ~b tiene una inclinación de (28.2 + 105)o con respecto al eje +x. Con esto resulta:
~b = 12.7 cos(133.2o )ı̂ + 12.7 sin(133.2o )̂ = −8.694ı̂ + 9.258̂.
Conocidas las componentes de ~a y ~b (formas canónicas), podemos calcular la suma:
~r = ~a + ~b = (11.19 + (−8.694))ı̂ + (6.001 + 9.258)̂ = 2.50ı̂ + 15.3̂.
Finalmente calculamos el módulo y la dirección de ~r:
||~r|| =
p
2.502 + 15.32 = 15.5.
15.3
θ = arctan
2.50
µ
¶
= 80.7o .
(VIII) Quiz #1, Ejercicio I.
~ y B:
~ El vector A
~ tiene una magnitud de 7 y está orientado 45o en dirección NorConsidere los vectores A
~ = 8ı̂ − 3̂. Calcule (a) las componentes en “X” y “Y ” de A,
~ (b) el vector A
~ + B,
~
Este, mientras queda B
~ − A,
~ y (d) la cantidad A
~ • B̂.
(c) la magnitud y dirección del vector B
Solución.- Como el ángulo de orientación está dirgido desde el Norte hacia el Este, las componentes del
~ (forma canónica) se hallan como:
vector A
~ = 7 sin(45o )ı̂ + 7 cos(45o )̂ = √7 ı̂ + √7 ̂ = √7 (ı̂ + ̂).
A
2
2
2
En la parte (b) la suma se calcula como:
~+B
~ =
A
µ
7
√ + 8 ı̂ +
2
¶
µ
7
√ − 3 ̂,
2
¶
mientras que en la parte (c) la resta se calcula como:
~ ≡B
~ −A
~ = 8 − √7 ı̂ + −3 − √7 ̂.
C
2
2
¶
µ
µ
¶
~ resultan:
La magnitud y dirección del vector C
~ =
||C||
sµ
¶2
s
70
7 2
+ 3+ √
= 122 − √ ≈ 8.5,
2
2
Ã
!
√
−3 2 − 7
√
θ = arctan
≈ −69o .
8 2−7
7
8− √
2
¶
µ
~ (B̂) es necesario primero calcular el módulo de dicho vector:
Para calcular el unitario de B
~ =
||B||
p
82 + 32 =
√
73,
~ es:
con ello resulta que la forma canónica del unitario de B
B̂ =
~
8ı̂ − 3̂
8
3
B
= √ ı̂ − √ ̂.
= √
~
73
73
73
||B||
Y finalmente realizamos el producto escalar de la parte (d):
~ • B̂ =
A
µ
7
7
√ ı̂ + √ ̂ •
2
2
¶
µ
3
7×8
7 × −3
35
8
√ ı̂ − √ ̂ = √ √ + √ √ = √
≈ 2.9
73
73
2 73
2 73
146
¶
(IX) Quiz #1, Ejercicio II.
Una partı́cula parte desde el reposo y desde el origen de un sistema de coordenadas con una aceleración
constante de 10m/s2 . (a) ¿Cuánto tiempo pasará hasta que la partı́cula recorre una distancia de medio
kilómetro?. (b) ¿Cuánto tiempo pasará hasta que la partı́cula adquiere una velocidad de 30km/h?. (c)
¿Qué distancia habrá recorrido después de minuto y medio?. (d) ¿Qué distancia recorrerá hasta que la
partı́cula adquiera una velocidad de 20km/h?.
Solución.- Como datos generales del problema tenemos la posición inicial x0 = 0m (parte del origen),
velocidad inicial v0 = 0m/s (parte del reposo) y la aceleración a = 10m/s2 .
En la pregunta (a) se tiene como un dato particular la posición final x = 500m, con la que se puede calcular
el tiempo de recorrido mediante la ecuación x = x0 + v0 t + 21 at2 :
1
x = at2
2
⇒
t=
r
2x
=
a
s
2 × 500m
= 10s.
10m/s2
Luego, en la parte (b) se tiene como dato particular la velocidad final de v = 30km/h = (25/3)m/s. El
tiempo transcurrido hasta alcanzar esta velocidad puede hallarse de la ecuación v = v0 + at:
v = at
⇒
t=
(25/3)m/s
5
v
=
= s ≈ 0.83s.
2
a
10m/s
6
De la parte (c) se tiene un tiempo de recorrido t = 90s y para calcular el tramo de dicho recorrido utilizamos
la misma ecuación que en la parte (a):
1
1
x = at2 = (10m/s2 )(90s)2 = 40500m = 40.5km
2
2
De la parte (d) se tiene una velocidad final v = 20km/h = (50/9)m/s y se pide encontrar el recorrido. Para
este caso empleamos la ecuación v 2 = v02 + 2a(x − x0 ), resultando:
v 2 = 2ax
⇒
x=
((50/9)m/s)2
125
v2
=
=
m ≈ 1.54m.
2a
2 × 10m/s2
81
(X) Tarea #2, Ejercicio I.
~ B
~ y C:
~ El vector A
~ tiene una magnitud de 5 unidades y está orientado 45o
Considere los vectores A,
~ tiene una magnitud de 11 unidades y está orientado 30o en dirección
en dirección Nor-Oeste; el vector B
~ = −ı̂ + 7̂. Calcule: (a) las componentes en “X” y “Y ” de los vectores A
~ y
Sur-Este; y por último C
~ (b) los vectores unitarios de A,
~ B
~ y C.
~ (c) la gráfica del plano cartesiano con los vectores A,
~ B
~ yC
~
B.
~ =C
~ − (Â + B).
~ (e) E
~ = (A
~ • C)
~ B̂. (f ) la magnitud y dirección de F~ = (B
~ − A)
~ × Ĉ.
(1cm = 1u). (d) D
(g) G =
~ B
~
A•
3
~
− 5||B̂ × C||.
~ y B
~ es necesario tener en cuenta la dirección cardinal que
Solución.- Para calcular las compentes de A
~ se encuentra orientado desde el Norte hacia el Oeste, por lo
tienen cada uno de estos vectores. El vector A
tanto
~ = −5 sin(45o )ı̂ + 5 cos(45o )̂ = − √5 ı̂ + √5 ̂ ≈ −3.54ı̂ + 3.54̂,
A
2
2
~ está orientado desde el Sur hacia el Este, lo que implica
mientras que el vector B
√
11
11 3
o
o
~
B = 11 sin(30 )ı̂ − 11 cos(30 )̂ = ı̂ −
̂ ≈ 5.50ı̂ + 9.53̂.
2
2
La siguiente figura muestra la representación de estos vectores en el plano cartesiano.
Los vectores unitarios se calculan como:
 =
B̂ =
Ĉ =
− √52 ı̂ +
~
A
=
~
5
|A|
√5 ̂
2
−1
1
= √ ı̂ + √ ̂ ≈ −0.71ı̂ + 0.71̂,
2
2
√
√
11
~
ı̂ − 112 3 ̂
B
3
1
= 2
= ı̂ −
̂ ≈ 0.50ı̂ − 0.87̂,
~
11
2
2
|B|
~
−1
C
−ı̂ + 7̂
7
= √ ı̂ + √ ̂ ≈ −0.14ı̂ + 0.99̂.
=√
2
2
~
50
50
1 +7
|C|
Nótese que |Â| = |B̂| = |Ĉ| = 1, y que si graficamos estos vectores unitarios en el plano cartesiano, quedarı́an
sobre sus respectivos vectores ordinarios.
~ puede calcularse de la siguiente forma:
El vector D
~ = C
~ − (Â + B)
~
D
~ = −ı̂ + 7̂ −
D
~ =
D
Ã
√ !
1
11
11 3
−1
√ ı̂ + √ ̂ + ı̂ −
̂
2
2
2
2
!
Ã
√ !
1
11
11 3
ı̂ + 7 − √ +
̂
−
2
2
2
Ã
1
−1 + √
2
~ ≈ −5.79ı̂ + 15.82̂.
D
~ se puede calcular por partes
El vector E
~•C
~ =
A
−5
5
40
√ × (−1) + √ × 7 = √
2
2
2
Ã
√ !
r
20
40 1
3
3
~
~
~
ı̂ −
̂ = √ ı̂ + 20
̂
E = (A • C)B̂ = √
2
2
2 2
2
~ ≈ 14.14ı̂ + 24.49̂.
E
Mientras que el vector F~ se calcula como:
Ã
!
√
11
5
11
5
3
~ −A
~ =
ı̂ −
̂ − − √ ı̂ + √ ̂ ,
B
2
2
2
2
!
à √
!
Ã
11 3
5
5
11
~
~
+ √ ı̂ −
+ √ ̂,
B−A =
2
2
2
2
~ −A
~ ≈ 9.04ı̂ − 13.06̂.
B
¯
¯
ı̂
¯
¯
~ − A)
~ × Ĉ ≈ ¯ 9.04
F~ = (B
¯
¯
¯ −0.14
̂
¯
k̂ ¯¯
¯
−13.06 0 ¯¯ = 7.10k̂.
0.99
¯
0 ¯
La magnitud de F~ es aproximadamente 7.10 y la dirección es sobre el eje z positivo (+k̂).
Por último, calculamos la cantidad escalar G como:
√
√
3
5
−55
11
−11
−5
~•B
~ =√ ×
+√ ×
= √ (1 + 3) ≈ −53.13.
A
2
2
2
2
2 2
¯
¯ ı̂
̂
¯
¯
~
¯
B̂ × C ≈ ¯ 0.50 0.87
¯
¯ −1
7
~ ≈ 4.37, al final tenemos
Debido a que ||B̂ × C||
G=
¯
k̂ ¯¯
¯
0 ¯¯ = 4.37k̂
¯
0 ¯
~•B
~
A
~ ≈ −53.13 − 5 × 4.37 = −39.54.
− 5||B̂ × C||
3
3
(XI) Tarea #2, Ejercicio II.
Un proyectil parte del reposo con una rapidez inicial de v0 = ||~v0 || = 50m/s y con una inclinación de
35o arriba del suelo. Si sólo el suelo detiene el movimiento del proyectil (en caı́da), calcule: (a) El vector
velocidad final y la rapidez final. (b) La altura máxima y alcance horizontal. (c) El tiempo de vuelo. (d)
Los tiempos para los que el proyectil se encuentra a un tercio de su altura máxima. (e) El tiempo para el
cual el proyectil ha recorrido horizontalmente dos tercios del alcance. (f ) El vector velocidad a un cuarto
del tiempo de vuelo. (g) El vector posición a tres cuartos del tiempo de vuelo.
Solución.- Las ecuaciones de cinemática bidimiensional con aceleraciones constantes son
1
x(t) = xo + vox t + ax t2 ,
2
1
x(t) = xo + t(vx + vox ),
2
vx (t) = vox + ax t,
1
y(t) = yo + voy t + ay t2 ,
2
1
y(t) = yo + t(vy + voy ),
2
vy (t) = voy + ay t,
2
vx2 (x) = vox
+ 2ax (x − xo ),
2
vy2 (y) = voy
+ 2ay (y − yo )
En cualquier instante del tiempo t, los vectores posición y velocidad en 2D están dados por
~r(t) = x(t)ı̂ + y(t)̂,
~v (t) = vx (t)ı̂ + vy (t)̂.
En un movimiento parabólico se tiene ax = 0 y ay = −g (donde g = 9.8m/s2 ). Además, si colocamos el
origen de coordenadas en el lugar donde comienza el movimiento (xo = yo = 0), las ecuaciones de cinemática
se simplifican como:
x(t) = vox t,
(1)
vx (t) = vox ,
(2)
1
y(t) = voy t − gt2 ,
2
1
t(vy + voy ),
y(t) =
2
vy (t) = voy − gt,
vy2 (y)
2
voy
=
(3)
(4)
(5)
− 2gy,
(6)
Ahora, con estas ecuaciones calculemos primero el tiempo de vuelo. Utilizando la ecuación 3 imponemos la
condición de que la partı́cula está en el suelo (y = 0)
1
0 = voy t − gt2
2
1
0 = t voy − gt ,
2
µ
⇒
¶
la cual es una ecuación cuadrática con 2 posibles valores de t. El primer valor es t = 0, que es cuando se
inicia el movimiento; mientras que el segundo es cuando
1
voy − gtv = 0
2
⇒
tv =
2voy
2vo sin θ
2 × 50m/s × sin(35o )
=
=
= 5.85s,
g
g
9.8m/s2
que es el tiempo en el cual la partı́cula llega al suelo nuevamente o tiempo de vuelo. Con tv hallamos la
velocidad en “Y ” con la que la particula pega al suelo. Para ello utilizamos la ecuación 5
vy (tv ) = voy − gtv = voy − g
µ
2voy
g
¶
= −vo sin θ = −28.68m/s.
Ya que vx = vox = v0 cos θ = 40.96m/s, el vector velocidad en el momento de impacto con el suelo es
~v (tv ) = (40.96ı̂ − 28.68̂)m/s.
Con este mismo tv y la ecuación 1 se halla el alcance o desplazamiento horizontal máximo L = x(tv )
L = vox tv = v0 cos θ
v 2 sin(2θ)
2vo sin θ
= o
= 239.7m,
g
g
Mientras que la altura máxima (H) la calculamos imponiendo vy = 0 en la ecuación 6
2
0 = voy
− 2gH
⇒
H=
2
voy
v 2 sin2 θ
= o
= 41.96m.
2g
2g
Para encontrar los tiempos en los que la partı́cula está a un tercio de la altura máxima, volvemos a utilizar
la ecuación 3 con y(tH/3 ) = H/3, es decir
H
1
= voy tH/3 − g(tH/3 )2
3
2
3g(tH/3 )2 − 6voy tH/3 + 2H = 0,
⇒
donde la solución con tH/3 es
tH/3 =
−(−6voy ) ±
q
(−6voy
2(3g)
)2
− 4(3g)(2H)
=
6voy ±
r
2 − 24g
36voy
6g
³ v2 ´
oy
2g
=
(6 ±
√
12)voy
1 voy
= 1± √
.
6g
3 g
µ
Lo que quiere decir que tH/3 puede ser igual a 1.24s ó 4.62s (subida y bajada respectivamente).
¶
Para encontrar el tiempo en el cual la partı́cula ha recorrido dos tercios del alcance L, recurrimos a la
ecuación 1 con x(t2L/3 ) = 2L/3, es decir
2L
= vox t2L/3
3
⇒
t2L/3 =
2L
=
3vox
³
2
2v02 sin θ cos θ
g
3vo cos θ
´
=
4vo sin θ
= 3.90s.
3g
Por otro lado, la velocidad en “Y ” en un cuarto del tiempo de vuelo es (ecuación 5)
vy (tv /4) = voy − g
tv
2voy
vo sin θ
= voy − g
=
= 14.34m/s.
4
4g
2
El vector velocidad en este caso es
~v (tv /4) = (40.96ı̂ + 14.34̂)m/s.
Para calcular el vector posición a tres cuartos del tiempo de vuelo, calculamos cada componente por separado
[x(3tv /4) , y(3tv /4)]. Dichas componentes resultan de las ecuaciones 1 y 3 respectivamente
3tv
3L
3v 2 sin(2θ)
=
= o
= 89.89m,
4
4
8g
µ
¶
1 3tv 2 3vo2 sin2 θ
3tv
− g
= 31.47m,
=
y(3tv /4) = voy
4
2
4
8g
~r(3tv /4) = (89.89ı̂ + 31.47̂)m.
x(3tv /4) = vox
(XII) Tarea #2, Ejercicio III. Sears-Zemansky 11va.Edición, Problema ∼3.27.
Un avión vuela con una velocidad de 90.0m/s y un ángulo de 16.0o debajo de la horizontal. Cuando está
114m directamente arriba de un perro parado en el suelo plano, se cae una maleta del compartimiento de
equipaje. (a) ¿A qué distancia del perro caerá la maleta?. (b) ¿Cuál es la rapidez de la maleta al chocar
con el suelo?. Haga caso omiso de la resistencia del aire.
Solución.- Coloquemos el origen del sistema de coordenadas donde está parado el perro, tal como se muestra en la figura. Debido a ello, las ecuaciones de cinemática bidimensional (presentadas al principio del
problema anterior) quedan como sigue
x(t) = vox t,
(7)
vx (t) = vox ,
(8)
1
y(t) = yo + voy t − gt2 ,
2
1
y(t) = yo + t(vy + voy ),
2
vy (t) = voy − gt,
2
vy2 (y) = voy
− 2g(y − yo ),
(9)
(10)
(11)
(12)
vox = +vo cos θ = 86.5m/s,
voy = −vo sin θ = −24.8m/s.
Nótese que la única ecuación que sirve para hallar la distancia a la que caerá la maleta es la ecuación
7. Sin embargo, en ella está explı́cita el tiempo (en nuestro caso serı́a el tiempo de vuelo, tv ). Para hallar
el tiempo desde que sale la maleta del avión hasta que llega al suelo utilizamos la ecuación 9 e imponemos
y = 0 (que llega al suelo)
1
0 = yo + voy tv − gt2v
2
⇒
tv =
−voy ±
q
2 − 4(− 1 g)y
voy
o
2
2(− 12 g)
=
−voy ±
q
2 + 2gy
voy
o
−g
.
Numéricamente tomamos el signo negativo de “±” y resulta
tv =
−(−24.8m/s) ±
p
(−24.8m/s)2 + 2(9.8m/s2 )(114m)
= 2.916s.
−9.8m/s2
Con este tiempo de vuelo calculamos la posición de la maleta cuando llega al suelo
x(tv ) = vox tv = (86.5m/s)(2.916s) = 252.3m.
La rapidez de impacto es la rapidez para el tiempo de vuelo. La velocidad en “X” para cualquier valor de t
es igual a vox ; mientras que en “Y ”
vy (tv ) = voy − gtv = −24.8m/s − (9.8m/s2 )(2.916s) = −53.4m/s.
Por lo tanto, la rapidez queda
||~v (tv )|| =
q
(86.5m/s)2 + (−53.4m/s)2 = 101.7m/s.
(XIII) Tarea #2, Ejercicio IV. Resnick 4ta.Edición, Capı́tulo 4, Problema 49.
Un avión antitanques está ubicado en el borde de una meseta a una altura de 60.0m sobre la llanura que lo
rodea. La cuadrilla de cañón avista un tanque enemigo estacionado en la llanura a una distancia horizontal
de 2.20km del cañón. En el mismo instante, la tripulación del tanque ve el cañón y comienza a escapar
en lı́nea recta de éste con una aceleración de 0.900m/s2 . Si el cañón antitanques dispara balas con una
velocidad de salida de 240m/s y un ángulo de elevación de 10o sobre la horizontal, ¿cuánto tiempo esperarán
los operadores del cañón antes de disparar para darle al tanque?
Solución.- Definamos a tE como el tiempo de espera del cañón, de forma que el tiempo total de la bala
desde que el tanque comienza a escapar hasta que la bala impacta con el tanque es
ttotal = tE + tv ,
donde tv es el tiempo de vuelo de la bala. Si colocamos el origen del sistema de coordenadas en el suelo
abajo del cañón, las ecuaciones de cinemática bidimensional de la bala quedan exactamente igual que en
el problema anterior (ecuaciones 7-12), puesto que en ambos casos la partı́cula inicia su movimiento a una
cierta altura del origen. Con la ecuación 9 podemos encontrar el tiempo de vuelo imponiendo y = 0
1
0 = yo + voy tv − gt2v
2
⇒
tv =
−voy ±
q
2 − 4(− 1 g)y
voy
o
2
2(− 12 g)
=
−voy ±
q
2 + 2gy
voy
o
−g
Como voy = vo sin θ = 41.68m/s, el resultado numérico de tv da
tv =
−41.68m/s ±
p
(41.68m/s)2 + 2(9.8m/s2 )(60m)
= 9.76s.
−9.8m/s2
De igual forma, con la ecuación 7 podemos encontrar el punto de impacto como L = x(tv )
L = vox tv = (240m/s) cos(10o )(9.76s) = 2306.8m.
.
Respecto al tanque, las ecuaciones que rigen su movimiento son
1
x̃(t) = x̃o + at2 ,
2
1
x̃(t) = x̃o + tṽx ,
2
ṽx (t) = at,
ṽx2 (x) = 2a(x̃ − x̃o ),
(13)
(14)
(15)
(16)
donde x̃o = 2200m, a = 0.9m/s2 y se ha impuesto ṽxo = 0. Sin sufrir mucho podemos calcular el tiempo
que tarda en llegar el tanque al punto de impacto (ti ) utilizando la ecuación 13 e imponiendo x̃(ti ) = L
1
L = x̃o + at2i
2
⇒
ti =
s
2(L − x̃o )
=
a
s
2(2306.8m − 2200m)
= 15.406s.
0.900m/s2
Puesto que la bala y el tanque deben tardar lo mismo en llegar al punto de impacto, el tiempo que tarda la
bala (ttotal ) y el tiempo que tarda el tanque (ti ) deben ser iguales
tE + tv = ti
⇒
tE = ti − tv = 15.406s − 9.79s = 5.65s
(XIV) El coyote intentando atrapar al correcaminos.
El coyote camina por una carretera a una velocidad de 1m/s en dirección norte. Por detrás de él viene un
correcaminos corriendo al doble de la velocidad. Cuando el correcaminos está 4m de distancia del coyote,
este último se percata pero mantiene su estado de movimiento. Cuando el correcaminos da alcance al coyote
y lo deja atrás, éste instantáneamente comienza a acelerar a 0.2m/s2 para intentar alcanzar al correcaminos.
(a) ¿Cuánto tiempo transcurre desde que el coyote se percata del acercamiento del correcaminos hasta que
los dos se encuentran?. (b) Realice los cálculos necesarios para determinar si el coyote pudo dar alcance al
correcaminos.
Solución.- Para la parte (a), resulta conveniente colocar el origen en la posición del correcaminos cuando
se percata del coyote. En ese momento, el correcaminos tendrá una posición inicial xo = 0m, mientras que
el coyote x̃o = 4m, de forma que las posiciones en función del tiempo para ambos quedan:
x(t) = vo t,
(Correcaminos)
x̃(t) = x̃o + ṽo t.
(Coyote)
El momento en que los dos se encuentran se halla con x(t) = x̃(t):
vo t = x̃o + ṽo t
⇒
t=
4m
x̃o
=
= 4s
vo − ṽo
2m/s − 1m/s
Ahora bien, como en la parte (b) el coyote trata de alcanzar al correcaminos cambiando su movimiento con
una determinada aceleración, necesitamos recolocar el origen del sistema de coordenadas en el lugar donde
el correcaminos intercepta al coyote (parte (a)). Con este nuevo origen las posiciones en función del tiempo
quedan:
x(t) = vo t,
(Correcaminos)
1
x̃(t) = ṽo t + ãt2 ,
2
(Coyote)
Obviamente, el coyote alcanzó al correcaminos puesto que el coyote estuvo aumentando su velocidad sin
algún lı́mite, y el tiempo en el que ésto ocurrió puede hallarse en la intersección x(t) = x̃(t):
1
vo t = ṽo t + ãt2
2
⇒
t=
2(vo − ṽo )
2(2m/s − 1m/s)
=
= 10s.
a
0.2m/s2
(XV) Sears-Zemansky 11va.Edición, Problema 3.63 (Salto del rı́o II).
Un profesor de fı́sica hacı́a acrobacias audaces
en su tiempo libre. Su última acrobacia fue un
un intento por saltar un rı́o en motocicleta (ver
Figura). La rampa de despegue está inclinada
53.0o , el rı́o tiene 40.0m de anchura y la ribera
lejana está 15.0m bajo el tope de la rampa. El
rı́o está 100m abajo de la rampa. Puede despreciarse la resistencia del aire. (a) ¿Qué rapidez
se necesita en el tope de la rampa para alcanzar
apenas el borde de la ribera lejana?. (b) Si su
rapidez era sólo la mitad del valor obtenido en
(a), ¿dónde cayó?.
Solución.- Para la parte (a) coloquemos el origen justo donde termina la rampa y la moto despega. Con
este sistema de coordenadas la posición inicial es xo = yo = 0m y la posición en la que deseamos que llegue
la moto es xf = 40.0m y yf = −15.0m (el signo negativo de yf se debe a que la moto caerá a una altura
negativa desde nuestro sistema de referencia). Ası́ pues, las ecuaciones de movimiento de la moto son:
x(t) = (vo cos θ)t,
vx (t) = vo cos θ,
1
y(t) = (vo sin θ)t − gt2 ,
2
1
t(vy + vo sin θ),
y(t) =
2
vy (t) = vo sin θ − gt,
vy2 (x) = (vo sin θ)2 − 2gy.
(17)
(18)
(19)
(20)
(21)
(22)
El tiempo de vuelo (tv ) se obtiene al imponer que la moto ha llegado al punto final en las ecuaciones 17 y
19 simultáneamente, es decir
xf
= (vo cos θ)tv ,
(23)
yf
1
= (vo sin θ)tv − gt2v .
2
(24)
En la primera de estas dos ecuaciones se despeja tv y ese valor algebraico se introduce en la segunda, con lo
que resulta
yf = xf tan θ −
gx2f
,
2vo2 cos2 θ
que es la ecuación de la trayectoria de la moto. De esta ecuación se despeja vo
xf
vo =
cos θ
s
g
40.0m
=
2(xf tan θ − yf )
cos(53.0o )
s
9.8m/s2
= 17.83m/s.
2[40.0m × tan(53.0o ) − (−15.0m)]
Para la parte (b) retomemos las ecuaciones 23 y 24. Sabemos que con vo ≥ 17.83m/s la moto llega al menos
al bore de la ribera y que con alguna otra rapidez inicial (ṽo ) menor a vo , la moto cae al rı́o. Con el sistema
de referencia de la parte (a) el rı́o está en y = −100m, por lo tanto, imponiendo que la rapidez inicial sea
ṽo < vo (ej: ṽo = vo /2) y la posición en “Y ” sea igual a ỹf = −100m podemos encontrar un nuevo tiempo
de vuelo, t̃v (desde que la moto sale de la rampa hasta que cae al rı́o) de la ecuación 24 como
1
ỹf = (ṽo sin θ)t̃v − g(t̃v )2
2
1
g(t̃v )2 − (ṽo sin θ)t̃v + ỹf = 0,
2
⇒
cuya solución es
t̃v =
ṽoy ±
q
(ṽoy )2 − 2g ỹf
g
,
ṽoy ≡
vo
sin θ = 7.12m/s.
2
Con el signo positivo del “±”, numéricamente resulta
t̃v =
7.12m/s ±
p
(7.12m/s)2 − 2(9.8m/s2 )(−100m)
= 5.30s.
9.8m/s2
Introduciendo este tiempo de vuelo en la ecuación 23, obtenemos la posición en “X” en el rı́o como
x̃f = (ṽo cos θ)t̃v = 56.87m.
Es decir que la moto cayó al rı́o a una distancia de 56.87m desde la pared del precipicio donde saltó el
profesor de fı́sica con la moto.
(XVI) Sears-Zemansky 11va.Edición, Problema 3.30.
Un modelo de rotor de helicóptero tiene cuatro aspas, cada una de 3.20m de longitud desde el eje central
hasta la punta. El modelo se gira en un túnel de viento a 550rpm. (a) ¿Qué rapidez lineal tiene la punta
del aspa en m/s?. (b) ¿Qué aceleración radial tiene la punta del aspa, expresada como un múltiplo de g?
Solución.- Las siglas rpm quieren decir “revoluciones por minuto” o “vueltas por minuto”. Con una simple
regla de tres podemos averigüar el tiempo en dar una vuelta (periodo, T )
500 vueltas
→
1 vuelta
→
1 min
1 vuelta × 1 min
T =
= 0.002 min = 0.12s.
500 vueltas
La rapidez lineal se calcula teniendo una longitud de arco, lo que en nuestro caso es toda la circunferencia
(S = 2πR). Por lo tanto, la rapidez lineal es
v=
S
2π × 3.20m
=
= 167.55m/s.
T
0.12s
El módulo de la aceleración radial en múltiplos de g es
( 2πR )2
v2
4π 2 R
4π 2 × 3.20m
ar
=
= T
=
=
= 895.20
g
gR
gR
gT 2
9.8m/s2 × (0.12s)2
⇒
ar = 895.20g.
(XVII) Sears-Zemansky 11va.Edición, Problema 3.31.
En una prueba de un “traje g”, un voluntario gira en un cı́rculo horizontal de 7.0m de radio. ¿Con qué
periodo la aceleración centrı́peta tiene magnitud de (a) 3.0g?, (b) ¿10g?.
Solución.- Del problema anterior tenemos v = 2πR/T , consecuentemente
4π 2 R
v2
=
ar =
R
T2
⇒
T = 2π
s
R
.
ar
Si ar = βg (donde β es un valor adimensional que indica cuantas veces la gravedad es la aceleración
centrı́peta) entonces
T = 2π
s
R
= 2π
βg
s
7.0m 1
5.31s
√ ≈ √
9.8m/s2 β
β
β = 3.0
⇒
T = 3.066s
β = 10
⇒
T = 1.679s
(XVIII) Sears-Zemansky 11va.Edición, Problema 3.32.
El radio de la órbita terrestre del Sol (suponiendo que fuera circular) es de 1.50 × 108 km, y la Tierra la
recorre en 365 dı́as. (a) Calcule la magnitud de la velocidad orbital de la Tierra en m/s. (b) Calcule la
aceleración radial hacia el Sol en m/s2 . (c) Repita las partes (a) y (b) para el movimiento del planeta
Mercurio (radio orbital = 5.79 × 107 km, periodo orbital = 88.0 dı́as).
Solución.- En metros el radio de la órbita terrestre del Sol es R = 1.50 × 1011 m, y un año en segundos es
igual a (con el dı́a bisiesto)
T = 365.25 × 24 × 60 × 60s = 31557600s.
Tomando el arco completo de la órbita, el módulo de la velocidad y la aceleración centrı́peta resultan
v =
ar =
2π × 1.50 × 1011 m
2πR
=
= 29865m/s,
T
31557600s
v2
(29865m/s)2
=
= 5.95 × 10−3 m/s2 .
R
1.50 × 1011 m
Para el plantea Mercurio (R = 5.79 × 1010 m y T = 7603200s) se tiene
v =
ar =
2π × 5.79 × 1010 m
= 47848m/s,
7603200s
(47848m/s)2
= 39.54 × 10−3 m/s2 .
5.79 × 1010 m