Tabla de integrales inmediatas - Página de Jaime Pinto Rodríguez
Anuncio

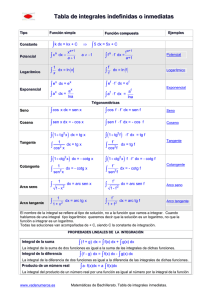
Tabla de integrales inmediatas: TABLA DE INTEGRALES INMEDIATAS Funciones simples Funciones compuestas dx x C k dx kx C n x dx x n 1 C n 1 n -1 1 x dx ln x C x e dx e x C n u u ' dx u n 1 C n 1 u' u dx ln u C e u u ' dx eu C ax a dx ln a C au a u ' dx ln a C cos x dx sen x C cos u u ' dx senu C sen x dx cos x C sen u u ' dx cos u C x 1 cos 2 (1 tg 2 (1 tg x) dx tg x C 1 2 1 2 2 1 1 u 2 dx arc cotg x C 1 u 1 x2 1 1 x 2 u) u' dx tg u C 1 dx arc tg x C 1 2 sen u u ' dx cotg u C 2 1 1 x 1 cos u u ' dx tg u C sen x dx cotg x C 1 x u dx tg x C x n -1 2 u ' dx arc tg u C 2 u ' dx arc cotg u C 1 dx arc sen x C dx arc cos x C 1 1 u2 1 1 u2 u ' dx arc sen u C u ' dx arc cos u C Integral Indefinida Dada una función f(x), decimos que la función F(x) es una primitiva de f(x) si se cumple: F'(x) = f(x). Se representa por: f ( x) dx F ( x) C Propiedades de la integral indefinida [ f ( x) g ( x)]dx f ( x) dx g ( x) dx Integración por sustitución El método de integración por sustitución consiste en introducir una variable t, que sustituye a una expresión apropiada en función de x, de forma que la integral se transforme en otra de variable t, más fácil de integrar. Integración por partes Integración de funciones racionales u dv u v v du *grado [P(x)] grado [Q(x)] P( x) R( x) Q( x) dx C (x) dx Q(x) dx * grado [P(x)] < grado [Q(x)] - si Q(x) tiene sólo raíces reales simples: P( x) A B M Q( x) dx x a dx x b dx ... x m dx - si Q(x) tiene raíces reales simples y múltiples: P ( x) A1 A2 Q( x) dx x a dx ( x a) 2 dx ... Ap ( x a) p dx Bp B1 B2 dx dx ... ( x b)q dx ... x b ( x b) 2 Mp M1 M2 dx dx ... ( x m)r dx xm ( x m) 2 - si Q(x) tiene una raíz real simple y dos complejas conjugadas: R ( x) A Mx N dx 2 qx r Q( x) dx x a dx px Integración de funciones circulares - Para calcular la primitiva sen m x cos n x dx , siendo n o m impares, hacemos el cambio sen x = t o cos x = t, respectivamente. - Para calcular la primitiva sen m x cos n x dx siendo n y m pares, la transformamos, utilizando las fórmulas del seno y coseno del ángulo doble, en otra más fácil de obtener.