Apertura hexagonal
Anuncio

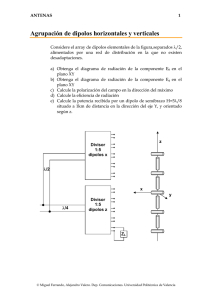
ANTENAS 1 Apertura hexagonal En la apertura hexagonal de lado a=4λ de la figura, los campos son uniformes y la polarización es horizontal. a) Calcular el campo radiado en la dirección del máximo y la potencia total radiada por la apertura. b) Calcular la Directividad y el Área efectiva. c) Obtener una expresión integral para el campo radiado en todo el espacio por la apertura. d) Calcular los campos radiados en el plano E. e) Calcular el diagrama de radiación en el plano H. G E = Ex xˆ G E H = H y yˆ = x yˆ η y E x Solución a Campo máximo Los campos radiados por una apertura con polarización horizontal son Eθ = j ⎛η ⎞ e − jkr jk y ' cos φ ⎜ cos θ + 1⎟ ∫∫ E ( x ', y ') e jk x x 'e y dx ' dy ' 2λ r ⎝ Z0 ⎠ s' Eφ = − j ⎛η ⎞ e − jkr jk y ' sin φ ⎜ + cos θ ⎟ ∫∫ E ( x ', y ' ) e jkx x 'e y dx ' dy ' 2λ r ⎝ Z0 ⎠ s' Si la apertura es uniforme, los campos radiados tendrán un máximo en la dirección del eje z. La relación de los campos en la apertura es la del espacio libre. kx = 0 k y = 0 Z0 = η e− jkr cos φ Ex A λr e− jkr sin φ Ex A Eφ = − j λr Eθ = j © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 2 En el eje z hay una indeterminación en la orientación de los ejes en coordenadas esféricas. En este caso es mejor representar la polarización del campo en cartesianas G e− jkr E= j E Axˆ λr x El área del hexágono se puede calcular dividiendo la figura en seis triángulos equiláteros ⎛1 3 ⎞ 3 2 A = 6 ⎜⎜ a a ⎟⎟ = 3 a 2 ⎝2 2 ⎠ Potencia total radiada La potencia se puede calcular a partir de la integración de la densidad de potencia en la misma Wt = ∫∫ s' Ex2 η ds ' = Ex2 η A Directividad Se ha visto que la directividad se puede calcular a partir de los campos en la apertura. D= 2 2 Pm 4π r 2 Eθ + Eφ = Wt Wt η 4π r 2 2 ⎛ ⎞ ⎜ ∫∫ Ea ( x ', y ') ds ' ⎟ 4π ⎠ D = 2 ⎝ s' 2 λ ∫∫ Ea ( x ', y ') ds ' s' Si la apertura es uniforme D= 4π λ 2 A Aef = A = 3 3 2 a 2 Campos radiados La integral doble de los campos es © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 3 ∫∫ E ( x ', y ') e jk x x ' e jk y y ' dx ' dy ' y s' Esta integral se puede reducir a una integral unidimensional. E x Si y(x) es el contorno del hexágono. a xmax ∫ xmin e jk x x ' xmax ⎛ ⎛ ymax ( x ) jk y ' ⎞ sin ( k y y ( x ) ) ⎞ ⎟dx ' ⎜ ∫ e y dy ' ⎟dx ' = ∫ e jk x x ' ⎜ y ( x ) ⎜ y ( x) ⎟ ⎜ ⎟ k y x ( ) y xmin ⎝ min ⎠ ⎝ ⎠ La fórmula se puede interpretar como una agrupación en x, de aperturas rectangulares como la marcada en la figura. Diagrama en el plano E El plano E es el XZ, en dicho plano k x = k sin (θ ) cos (φ ) = k sin (θ ) cos ( 0 ) = k sin (θ ) k y = k sin (θ ) sin (φ ) = k sin (θ ) sin ( 0 ) = 0 El diagrama será proporcional a la integral jk x ' ∫∫ E ( x ', y ') e x e s' jk y y ' dx ' dy ' = Ex xmax ∫ 2 y ( x )e jkx x ' dx ' xmin Esta integral es la transformada de Fourier del contorno, es decir de una función como un triángulo truncado La transformada de Fourier de dicha función se puede calcular por resta de dos triángulos equiláteros de lados 2a y a respectivamente. Dicha transformada es proporcional a las áreas de los triángulos. y a a a x © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 4 2 ⎛ ⎛ k x 2a ⎞ ⎞ ⎛ ⎛ kx a ⎞ ⎞ sin ⎜ sin ⎜ 4 ⎟ ⎟ 3 2 ⎜ ⎜⎝ 4 ⎟⎠ ⎟ ⎝ ⎠ 2 ⎟ − ⎟ F ( k x ) = 3a ⎜ a ⎜ 4 ⎜ k x 2a ⎟ ⎜ kx a ⎟ ⎜ ⎟ ⎜ ⎟ 4 4 ⎝ ⎠ ⎝ ⎠ 2 Los campos en el plano E son Eθ = j e − jkr ( cosθ + 1) 2 Ex F ( k x , a ) 2λ r Eφ = 0 Diagrama en el plano H El plano H es el YZ ⎛π ⎞ k x = k sin (θ ) cos (φ ) = k sin (θ ) cos ⎜ ⎟ = 0 ⎝2⎠ ⎛π ⎞ k y = k sin (θ ) sin (φ ) = k sin (θ ) sin ⎜ ⎟ = k sin (θ ) ⎝2⎠ ∫∫ E ( x ', y ') e s' jk x x ' e jk y y ' dx ' dy ' = Ex ymax ∫ 2 x ( y )e jk y y ' dy ' ymin El problema es similar al anterior del plano E, pero con una forma diferente para la función a transformar, que es x a a/2 Eθ = 0 Eφ = − j − jkr e (1 + cosθ ) 2 ExG ( k y , b ) 2λ r a/2 y a 3 La función a transformar es la suma de una función uniforme y un triángulo, ambas de la misma anchura, a 3 . La transformada es proporcional al área de las figuras G ( k y ) = a2 ⎛ ⎛ kya 3 ⎞ ⎞ ⎛ ⎛ kya 3 ⎞ ⎞ ⎜ sin ⎜ ⎜ sin ⎜ ⎟⎟ ⎟⎟ ⎜ ⎟ ⎜ ⎟⎟ 2 4 ⎜ ⎟ ⎜ 3 ⎝ ⎠ + 1 a2 3 ⎝ ⎠ ⎜ ⎟ ⎜ ⎟ 2 ⎜ kya 3 ⎟ 2 2 ⎜ kya 3 ⎟ ⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟ 2 4 ⎝ ⎠ ⎝ ⎠ 2 © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia