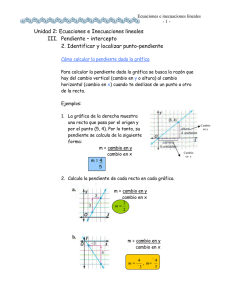
¿Cómo encontrar la pendiente?
Anuncio

Ecuaciones e inecuaciones lineales -1- Unidad 2: Ecuaciones e Inecuaciones lineales III. Pendiente – intercepto 2. Identificar y localizar punto-pendiente Cómo calcular la pendiente dada la gráfica Para calcular la pendiente dada la gráfica se busca la razón que hay del cambio vertical (cambio en y o altura) al cambio horizontal (cambio en x) cuando te deslizas de un punto a otro de la recta. Ejemplos: 1. La gráfica de la derecha muestra una recta que pasa por el origen y por el punto (5, 4). Por lo tanto, su pendiente se calcula de la siguiente forma: m = cambio en y cambio en x m=4 5 2. Calcula la pendiente de cada recta en cada gráfica. m = cambio en y cambio en x 3 m 2 m = cambio en y cambio en x m 4 4 , m 3 3 Cambio en y Cambio en x Ecuaciones e inecuaciones lineales -2m = cambio en y cambio en x m 0 2 m0 m = cambio en y cambio en x 3 m 0 No es posible dividir entre cero m es no definida Cómo calcular la pendiente dado dos puntos Para calcular la pendiente de dos puntos dados, se utiliza la siguiente fórmula: y y No importa cuál m 2 1 , donde x1 x 2 . x 2 x1 par ordenado se elija como ( x1 , y1 ) Ejemplo: Calcula la pendiente de la recta que pasa por (2, -5) Y (7, -10). Sea (2, -5) = ( x 1 , y 1 ) Y (7, -10) = ( x 2 , y 2 ) m y 2 y1 10 (-5) 5 10 5 5 1 m = -1 72 5 5 x 2 x1 Ecuaciones e inecuaciones lineales -3- Cómo calcular la forma punto-pendiente para un punto dado Para un punto dado x1 , y1 en una recta no vertical con pendiente m, la forma punto-pendiente de una ecuación lineal es: y y1 m( x x1 ) Se puede escribir una ecuación en la forma puntopendiente de la gráfica de cualquier recta no vertical si se conoce la pendiente de la recta y las coordenadas de un punto sobre la recta. Ejemplos: 1). Escribe la forma punto-pendiente de una ecuación para una recta que pasa por (-3, 5) con 3 pendiente . 4 y y1 m(x x1 ) 3 y 5 ( x -(-3)) (-3)) 4 y 5 3 ( x 3) 4 Se remplaza x1 por -3, y1 3 por 5 y m por . 4 Una ecuación de la recta es y 5 La gráfica es: 3 ( x 3) . 4 Ecuaciones e inecuaciones lineales -42). Escribe la forma punto-pendiente de la ecuación de una recta que pasa por (-8, 3) y (4, 5). Primero, calcular la pendiente de la recta. y y 53 2 1 m 2 1 x 2 x1 4(-8) 12 6 Segundo, usar cualquier punto como ( x1 , y1 ) en la forma punto-pendiente. Si usas (-8, 3): y y1 m(x x1 ) y3 1 ( x (-8)) 6 y 3 1 ( x 8) 6 Si usas (4, 5): y y1 m(x x1 ) y5 1 ( x 4) 6 Ambas ecuaciones son equivalentes.