4pp - Departamento de Informática - Universidad Técnica Federico

Universidad Técnica Federico Santa María
Universidad Técnica Federico Santa María
Variables Aleatorias
Departamento de Informática
ILI-280
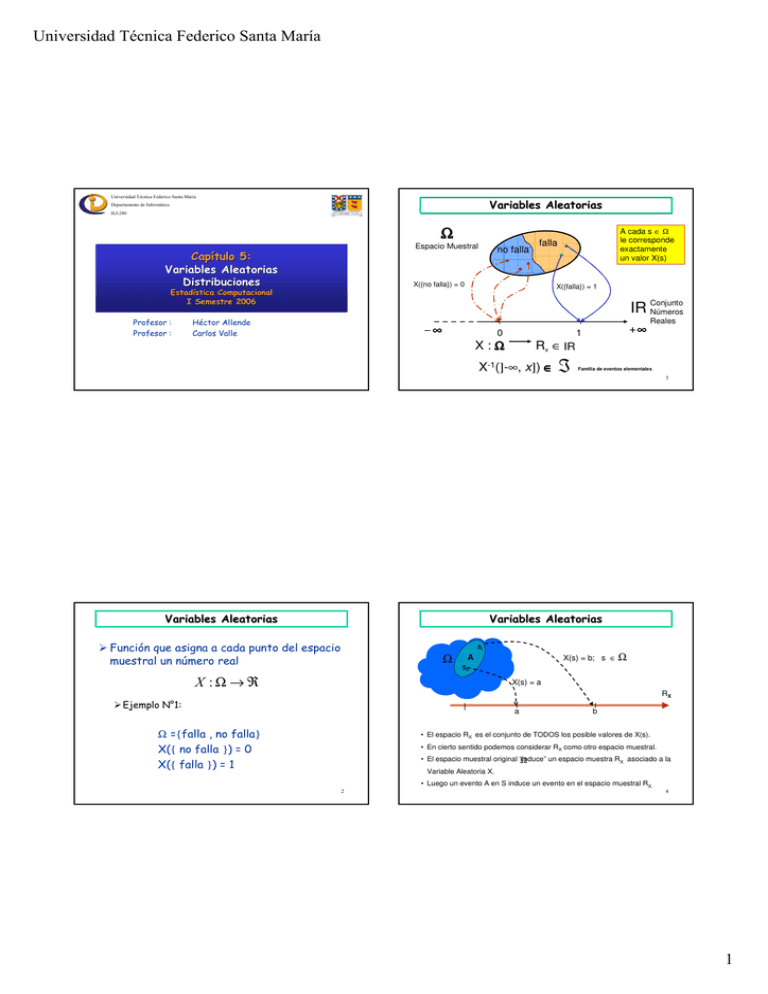
Ω
Espacio Muestral
Capítulo 5:
Variables Aleatorias
Distribuciones
no falla
X({no falla}) = 0
X({falla}) = 1
Estadística Computacional
I Semestre 2006
Profesor :
Profesor :
A cada s ∈ Ω
le corresponde
exactamente
un valor X(s)
falla
IR Conjunto
Números
Héctor Allende
Carlos Valle
−∞
0
+∞
1
X:Ω
Reales
Rx ∈ IR
X-1(]-∞,
x]) ∈
ℑ
Familia de eventos elementales
3
Variables Aleatorias
Variables Aleatorias
Función que asigna a cada punto del espacio
muestral un número real
si
Ω
X(s) = b; s ∈ Ω
A
sk
X :Ω → ℜ
X(s) = a
RX
Ejemplo N°1:
a
Ω ={falla , no falla}
X({ no falla }) = 0
X({ falla }) = 1
b
• El espacio RX es el conjunto de TODOS los posible valores de X(s).
• En cierto sentido podemos considerar RX como otro espacio muestral.
• El espacio muestral original “induce”
un espacio muestra RX asociado a la
Ω
Variable Aleatoria X.
• Luego un evento A en S induce un evento en el espacio muestral RX.
2
4
1
Universidad Técnica Federico Santa María
Variables Aleatorias
Variable Aleatoria
X :Ω →ℜ
si
X(s) = b; s ∈ Ω
A
X −1 (] − ∞, x ]) ∈ ℑ
sk
X(s) = a
RX
Nótese que
para cada
par de
números
reales a y b
existen los
siguientes
conjuntos
a
(
(
[
[
a<x<b
a<x≤b
a≤x<b
a≤x≤b
(
x<b
x≤b
x>a
(
x≥a
-∞
-∞
b
)
]
)
]
Sea C ∈ ℑ (con C ⊆ Ω) Soporte contable
f:C → ℜ
C = {ci : i ∈ I ⊆ N }
i) f (ci ) ≥ 0
ii)
)
]
7
Variable Aleatoria Discreta
Sea X una variable aleatoria
Si el número de valores de X (esto es su Recorrido).
Es finito (contable) o.
Es contablemente infinito (denumerable).
Entonces llamamos a X una variable aleatoria discreta.
Esto es, los valores de X (w) pueden ser enumerados.
x1, x2, x3, …, xn, …
0 ≤ P(X(s) = x ) = f(x) ≤ 1
f(x)
1
[0, 1]
RX
0
En el caso contable la lista es finita.
En el caso denumerable la lista es infinita contable
X(s) = x
s
X: Ω
i
Usando la transformacion X
∞
∞
El concepto de Probabilidad de ocurrencia
de eventos en el espacio muestral Ω se
puede aplicar a eventos en RX.
f: R
∑ f (c ) = 1
i∈I
Función de Probabilidad
Ω
Variable Aleatoria Discreta
RX
6
8
2
Universidad Técnica Federico Santa María
Variable Aleatoria Discreta
Función de Cuantía de una v.a. discreta
x(ci ) = xi
Sea C ∈ℑ , conjunto de eventos elementales de una familia
de eventos del espacio muestra; C ⊆ Ω
P( A) =
Sea A el evento tal los eventos elementales ci∈C pertnezcan
también a A, esto es ci ∈ C ∩ A. Usando la transformación
X:
∑
i
P( X = xi ) ≥ 0
∑ P( X = x ) = 1
i
i
Función de Distribución
x(ci ) = xi
F ( x) = ∑ P( X = xi ) = ∑ f ( xi )
f (c j ) = ∑ P ( X = xi )
j∈{i:ci ∈C ∩ A}
f (c j ) = ∑ P( X = xi )
Propiedades función de cuantía:
p(ci ) = P(ci ) ≥ 0
P( A) =
∑
j∈{i:ci ∈C ∩ A}
es una función definida sobre el Espacio
Muestral, que mapea en el conjunto de los Números Reales
los eventos elementales definidos en C = { ci: i ∈ I ⊆ N }, tal
que:
X : C →ℜ
i
xi ≤ x
xi ≤ x
9
Función de Probabilidad v.a discreta
Esperanza y Varianza de una v.a. discreta
A cada resultado posible xi se
asocia un número
Esperanza de una v.a.d. X
E [ X ] = ∑ xi P ( X = xi )
f ( xi ) = P ( X ( s ) = xi )
llamado la probabilidad de xi
Los f(xi) deben satisfacer:
i
f(xi)
Varianza de una v.a.d X
0 ≤ f ( xi ) ≤ 1
V [X ] = ∑ ( xi − E [X ]) 2 P ( X = xi )
∑ f (x ) = 1
i
i
x
i
El conjunto de pares
(xi, f(xi)) se le denomina
Función de Probabilidad o
Cuantía.
11
x1 x2 x3 x4 x5 x6
xn
P (X=5) = f(5) Función de Probabilidad de “masa”
Función de Frecuencia
10
12
3
Universidad Técnica Federico Santa María
Distribución Bernoulli
Distribución Binomial
Consideremos un solo experimento ε
sea A un evento asociado con tal experimento.
supongamos que P(A) = p; luego P(Ac) = 1- p
Sea la v.a. X(A ) = 1
P(X = 1) = p
X(Ac) = 0
f(x)
Supongamos que de una línea de producción
se extraen n piezas con reemplazo, las
cuales pueden ser defectuosas o no con una
probabilidad “p”.
P(X = 0) = 1 – p
X: N° de piezas defectuosas en las n
extracciones
p = 0,7
Entonces
Entonces su función de
cuantía es
 n
P( X = k ) =   p k (1 − p) n −k
k 
f(x) = P(X =x) = px (1 – p)1-x
X = 0, 1
0<p<1
x
0
0
1
13
15
Distribución Bernoulli
Distribución Binomial
Variable aleatoria discreta Bernoulli:
• Sean n repeticiones independientes del experimento.
• Ω consiste de todos los posibles secuencias { a1, a2, a3, .., an},
donde cada ai puede ser un evento A o un evento Ac.
• Existen 2n de tales secuencias.
X :Ω → ℜ
Sea la variable aleatoria
X := número de veces que
ocurre el evento A
sus posibles valores son:
0, 1, 2, 3 , ....., n
donde se tienen sólo 2 eventos posibles:
P( X ( w) = 0) = 1 − p
f(x)
0,300
P( X ( w) = 1) = p
0,200
Esperanza:
Varianza:
k = 0,1,..., n
E [X] = 0 ( 1 - p ) + 1 * p = p
V [X] = ( 0 - p )2( 1 - p ) + ( 1 - p )2 p
=p(1-p)
n = 16
p = 0,2
f(x) = P(X = x) =
n
x
px (1 –p)n-x
0,100
0,000
14
x
0
1
2
3
4
5
6
7
8
9
x = 0, 1, 2,......,n
0<p<1
16
4
Universidad Técnica Federico Santa María
Distribución Binomial
Esperanza:
Varianza :
Notación:
Distribución Hipergeométrica
E [X] = np
V [X] = np (1-p)
Surge en poblaciones que contienen
elementos clasificables en 2 estratos (con
defectos: D ; sin defectos: N - D).
X ~ Bi ( n, p )
Características:
Se utiliza en el muestreo de una población finita
con reemplazo.
También cuando la población es muy grande, con
o sin reemplazo, ya que “p” se hace
relativamente constante.
Consideremos un lote de tamaño N. Se
extrae una muestra de tamaño n sin
reemplazo.
X: N° de artículos defectuosos en la muestra
17
19
Distribución Binomial
Distribución Binomial
 D  N − D
 k   n − k 

P( X = k ) =   
N
 
n
k =0,1,2,.....,min{
{ n,D}
E[X ] = n
D
N
V [X ] = n
D( N − D)( N − n)
N 2 ( N − 1)
Es aplicable al muestrear lotes de tamaño pequeño
en relación al tamaño de la muestra (N ≤ 10 n).
18
20
5
Universidad Técnica Federico Santa María
Distribución de Poisson
Distribución de Poisson
Supongamos que tenemos una muestra de
tamaño grande, para lo cual la probabilidad
de encontrar un artículo defectuoso es
pequeño “p”, y por lo tanto “np” el número
total de artículos defectuosos en la
muestra.
Sea λ = np.
Entonces
P( X = k ) =
λk e − λ
k!
Esperanza:
Varianza:
E [X] = λ
V [X] = λ
Caso límite: X ∼ B( n , p )
k
 n  λ   λ 
P( X = k ) =    1 − 
 k  n   n 
con
n −k
I (k )
{
}
0 ,1, 2 ,.... , n
n→∞ y p≈0
P( X = k ) =
k = 0,1,2,....
λk
k!
e −λ I N 0 ( k )
21
Distribución de Poisson
23
Construcción de un Modelo Probabilístico
Ejemplo:
Las piezas a la salida de una línea de producción se
clasifican en defectuosas (D) o no defectuosas (N).
Se toma tres piezas aleatoriamente y se clasifican de
acuerdo a este esquema. El Ω para este experimento es:
Ω = {NNN, NND, NDN, DNN, NDD, DND, DDN, DDD}
La probabilidad que una pieza sea defectuosa es p y no
cambia. Eso implica que si la población es finita, las
observaciones se hacen con reemplazo
Interesa el número de piezas D y no el orden en que
salen.
Se define una v.a. X igual al número de piezas
defectuosas; luego, X = { 0, 1, 2, 3). Encontrar (xi, f(xi))
22
24
6
Universidad Técnica Federico Santa María
Creando un modelo probabilístico
f(x)
Variables Aleatorias Continuas
Cuando el experimento ε se realiza sobre un espacio muestral
Ω que está relacionado con escalas intevalares.
tales como mediciones de distancias, volúmenes, pesos,
tiempos, velocidad, voltajes, intensidad, caudal,
temperatura, etc.
Ya que los posibles valores de X en un intervalo, a < x < b, son
infinitos - no enumerables - no podemos hablar del i-ésimo
valor de X = xi; En tales casos se habla de Variables
Aleatorias Continuas, donde Rx es un intervalo o un conjunto
de intervalos; entonces existe una función continua especial:
3(1-p)2p
0,5
(1-p)3
0,4
3(1-p) p2
0,3
0,2
p3
0,1
x
0
0
1
2
3
f :ℜ → ℜ
Ω = {NNN, NND, NDN, DNN, NDD, DND, DDN, DDD}
X(NND)= 1
X(NDN)= 1
X(DNN)= 1
f ( x) = lim
3 P(N) P(N) P(D)
h →0
P ( x < X < x + h)
>0
h
25
27
Función de distribución v.a. discreta
F(x)
F(x) = 0
Variables Aleatorias Continuas
x < x1
1
1
= Σ f( xi )
x1 ≤ x < x2
= Σ f( xi )
x2 ≤ x < x3
= Σ f( xi )
x3 ≤ x < x4
i=1
2
i=1
3
i=1
4
= Σ f( xi )
i=1
Sea X una variable
aleatoria continua. La
función densidad de
probabilidad (pdf) es
una función que
satisface:
f(x) > 0;
P(X=x5) = f(x5) Función de Probabilidad de “masa”
Función de Frecuencia
x3
x4
x5
x6
a
x
b
∀ x ∈ Rx ∈ −∞, +∞
A: { x| a < x ≤ b)
∫ f(x) dx = 1
x
x2
A: un evento
x4 ≤ x < x5
0
x1
f(x)
Rx
xn
26
b
P(A) = P(a < x < b) =
∫ f( x ) dx
a
28
7
Universidad Técnica Federico Santa María
Distribuciones de Probabilidad Continuas
Función de distribución acumulada
Están definidas por una densidad de v. a. X
Si X es una variable aleatoria, la Función de Distribución
Acumulada mide la probabilidad de un suceso en un intervalo de
valores:
f :ℜ → ℜ
se dice densidad de probabilidad
F ( x) = P( X ≤ x)
Propiedades:
Si X es una v.a. Discreta
Discreta
f(x) ≥ 0
F ( x) =
∞
Si X es una v.a. Continua
x
∑ f (x )
F ( x) =
i
∀i ∃xi ≤ x
∫ f(x)dx = 1
−∞
Donde la suma es tomada
sobre todos los índices i
que satisfacen xi ≤ x
-∞
∫ f (t )dt
Donde la sumatoria es
reemplazada por una
integración para todos
los valores de t ≤ x
29
31
Propiedades y Definiciones
Construcción de Modelos de Probabilidad
b
∫
1. P ( a ≤ x ≤ b) = f ( x) dx
a
2. F ( x ) = P ( X ≤ x) =
Sea F : ℜ → ℜ es una función de distribución,
entonces:
x
∫ f (t )dt
F es no decreciente
F es continua por la derecha
lim f ( x ) = 0 y lim f ( x ) = 1
−∞
3. F (-∞
∞) = 0 ; F (∞
∞) = 1
4. Fx es no decreciente
5. E [ X ] =
6.
x → −∞
b
A = ∫ f ( x)dx
f(x)
∫ xf ( x)dx
a
a
x
b
|R
V [X ] = ∫ ( x − E [X ]) 2 f ( x)dx
R
30
x →∞
Luego P(]] -∞
∞ , x ]) = F(x) define una Probabilidad
Además:
P( ]a,b]
P( [a,b]
P( ]a,b[
P( [a,b[
)=
)=
)=
)=
F(b) - F(a)
F(b) - F(a-)
F(b-) - F(a)
F(b-) - F(a-)
32
8
Universidad Técnica Federico Santa María
Variables Aleatorias Continuas
Sea X una variable aleatoria
continua que puede tomar
cualquier valor entre a ≤ x ≤ b;
cuya pdf es:
f (x) =
1
b−a
Distribución Uniforme
a≤ x≤b
f(x)
Sea a = 3; b = 12
0,2
A: el evento { 4 < x < 7 }
0,1
Entonces:
7
x
0,0
2 3 4 5 6 7
8 9 10 11 12
a
b
min
P(A) = P(4 < x < 7)
=
∫
1
9
dx
4
máx
1
P(A) =
3
33
Distribución Uniforme
Función de densidad
f ( x) =
1
b−a
Distribución Normal o Gaussiana
Función de densidad
a< x<b
f ( x) =
Función de Distribución es

0

 x − a
F ( x) = 
 b−a

1

a+b
Esperanza E [X ] =
2
Notación:
X ~ U ( a, b)
35
x≤a
1
2π σ
e
1  x−µ  2
− 

2 σ 
,x∈R
La función de Distribución no tiene expresión
analítica. (Usar tablas o calculadoras)
a< x<b
x≥b
(b − a) 2
Varianza V [X ] =
12
34
Esperanza E [ X ] = µ
Varianza
V [X ] = σ 2
Notación: X ~ N ( µ , σ 2 )
36
9
Universidad Técnica Federico Santa María
Distribución Normal
Distribución Exponencial
Función de densidad
f X ( x) =
1
λ
e
−
x
λ
x ≥ 0, λ > 0
si
Función de Distribución es
FX ( x) = 1 − e
−
x
λ
x≥0
E [X ] = λ
Esperanza
V [X ] = λ2
Varianza
Notación: X ~ exp(λ )
37
Distribución Normal o Gaussiana
39
Distribución Exponencial
Estandarización
Haciendo
Z=
se tiene que:
X − µ ∼ N( 0 , 1 )
σ
1
f z ( z) =
1 − 2 z2
e
2π
,z∈R
y FZ(z) se obtiene de tablas !
38
40
10
Universidad Técnica Federico Santa María
Distribución de Rayleigh
Distribución de Weibull
Función de densidad
f X ( x) =
x
−
α2
e
Función de densidad
x2
2α 2
si
f X ( x) = abx b −1e − ax
x≥0
Función de Distribución es
FX ( x) = 1 − e
Esperanza
Varianza
Notación:
E[ X ] =
−
x ≥ 0 , a > 0, b > 0
si
Función de Distribución es
x2
2α 2
b
FX ( x) = 1 − e − ax
x≥0
b
x≥0
 1
E [X ] = a −1 / b Γ1 + 
Esperanza
 b

2
1 
Varianza V [X ] = a −2 / b Γ1 +  − Γ 2 1 + 
 b 
  b
Notación: X ~ Weibull (a, b)
α 2π
2
π
V [ X ] = ( 2 − )α 2
2
X ~ R (α )
41
Distribución de Rayleigh
43
Distribución de Weibull
42
44
11
Universidad Técnica Federico Santa María
Distribución tt-student
Distribución Gamma
Función de densidad
Función de densidad
−
x
xα −1e β
f X ( x, α , β ) =
I R + ( x)
Γ(α ) β α
ν + 1 
Γ

1
2  1
f X ( x) = 
ν +1
 ν  νπ
Γ 
 x2  2


1
+
2
 
 ν 


Función de Distribución es
x
FX ( x) = P( X ≤ x) =
∫ f (t ,α , β )dt
−∞
Esperanza
Varianza
Notación:
E[ X ] = 0 ν > 1
V [X ] =
ν
ν −2
∞
Esperanza E [ X ] = αβ
Γ( n ) = ∫ y n −1e − y dy
2
V [ X ] = αβ
0
Varianza
Notación: X ~ Gamma(α , β ) = Γ(α , β )
ν >2
X ~ tν
45
Distribución tt-student
n>0
47
Distribución Gamma
X ~ Γ(α , β )
46
48
12
Universidad Técnica Federico Santa María
Distribución ChiChi-Cuadrado
Función de densidad
n
−1 −
Distribución Beta
Función de densidad
x
x2 e 2
f X ( x,n ) =
I (x)
n R+
n
Γ  2 2
2
f X ( x, r , s ) =
Función de Distribución es
x
∫
I[ ]( x)
0 ,1
1
Función de Distribución es
FX ( x) = P( X ≤ x) =
Γ( r + s ) r −1
x (1 − x ) s −1
Γ( r )Γ( s )
FX ( x ) = P( X ≤ x ) =
f (t , n) dt
−∞
Esperanza
Varianza
Esperanza E[ X ] = n
V [ X ] = 2n
Varianza
Notación: X ~ χ 2 (n) = Γ(n / 2,2)
Notación:
E[X ] =
r
r+s
β (r, s) = ∫ xr−1(1 − x)s−1 dx
−∞
µ
rs
V [X ] =
( r + s ) 2 ( r + s + 1)
X ~ Beta(r , s) = β (r , s)
49
Distribución ChiChi-Cuadrado
0
x
∫ f (u, r , s )du
Γ( r + s )Γ( r + u )
E [X ] =
Γ( r )Γ( r + s + u )
51
Distribución Beta
50
52
13