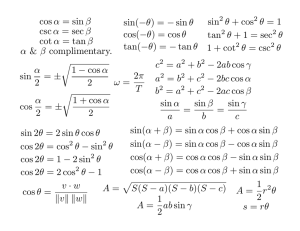Trigonometry Formulas
Anuncio

Trigonometry Formulas y 6 r r ... sin θ = (x, y) θ ... .. I y r cos θ = x r tan θ = y x -x sec θ = 1 cos θ csc θ = 1 sin θ tan θ = sin θ cos θ cot θ = cos θ sin θ C ... ......... ....... .. ....... .. ....... .... . . . . . . . ....... ... ....... ... ....... .. ....... .. ....... . . . . . . . . .. ....... ... ....... ... ....... .. ....... .. ....... . . . . . . . . . ....... ... ....... ... ....... ........................................................................................... Law of Sines: b b c a = = sin A sin B sin C a A c Law of Cosines: a2 = b2 + c2 − 2bc cos A B θ 30◦ (π/6) sin θ cos θ tan θ 1/2 √ 3/2 √ 3/3 45◦ (π/4) √ 2/2 √ 2/2 1 60◦ (π/3) √ 3/2 1/2 √ 3 Pythagorean Identities sin2 θ + cos2 θ = 1 1 + tan2 θ = sec2 θ 1 + cot2 θ = csc2 θ cos(−θ) = cos θ tan(−θ) = − tan θ Symmetry Identities sin(−θ) = − sin θ Sum and Difference Identities sin(α + β) = sin α cos β + cos α sin β cos(α + β) = cos α cos β − sin α sin β tan α + tan β tan(α + β) = 1 − tan α tan β sin(α − β) = sin α cos β − cos α sin β cos(α − β) = cos α cos β + sin α sin β tan α − tan β tan(α − β) = 1 + tan α tan β Double-Angle Identities cos 2θ = cos2 θ − sin2 θ = 1 − 2 sin2 θ sin 2θ = 2 sin θ cos θ 2 tan θ tan 2θ = 1 − tan2 θ = 2 cos2 θ − 1 Power-Reducing Identities 1 + cos 2θ cos2 θ = 2 Product-To-Sum Identities sin2 θ = 1 − cos 2θ 2 1 sin(α − β) + sin(α + β) 2 1 sin α sin β = cos(α − β) − cos(α + β) 2 1 cos α cos β = cos(α − β) + cos(α + β) 2 sin α cos β = Gilles Cazelais. Typeset with LATEX on April 29, 2006.