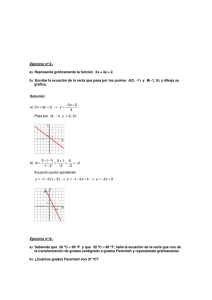
FUNCIONES CONCEPTO DE FUNCIÓN CONCEPTO DE FUNCIÓN
Anuncio
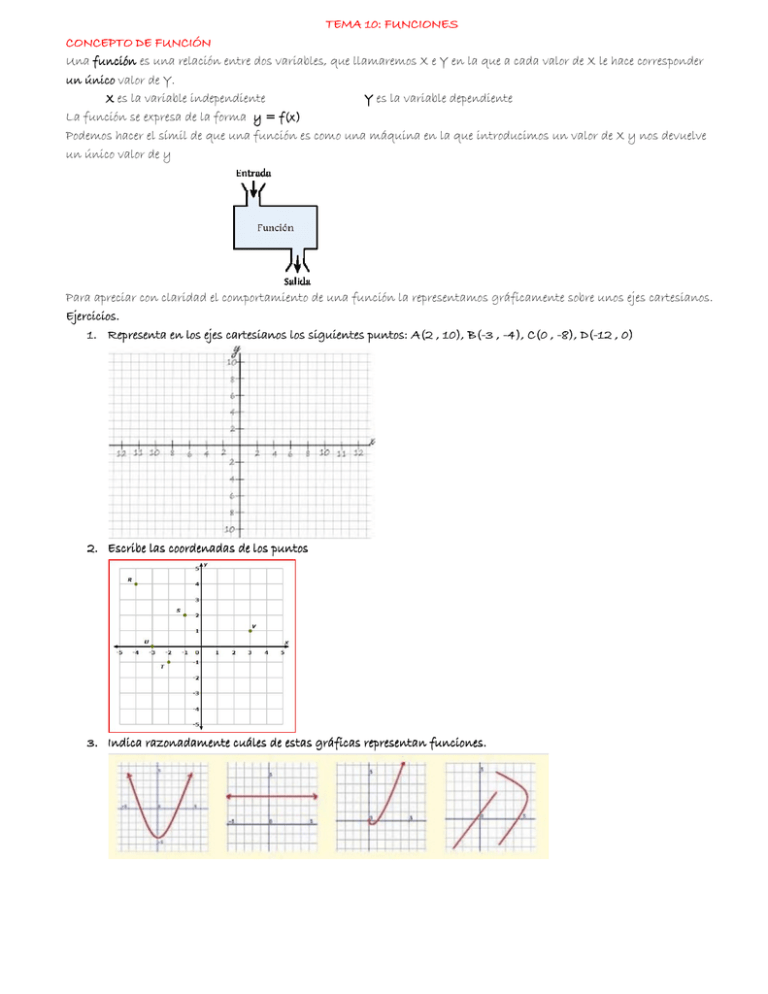
TEMA 10: FUNCIONES CONCEPTO DE FUNCIÓN Una función es una relación entre dos variables, que llamaremos X e Y en la que a cada valor de X le hace corresponder un único valor de Y. X es la variable independiente Y es la variable dependiente La función se expresa de la forma y = f(x) Podemos hacer el símil de que una función es como una máquina en la que introducimos un valor de X y nos devuelve un único valor de y Para apreciar con claridad el comportamiento de una función la representamos gráficamente sobre unos ejes cartesianos. Ejercicios. 1. Representa en los ejes cartesianos los siguientes puntos: A(2 , 10), B(B(-3 , -4), C(0 , -8), D(D(-12 , 0) 2. Escribe las coordenadas de los puntos 3. Indica razonadamente cuáles de estas gráficas representan funciones. 4. En las instrucciones de un medicamento, que hay que administrar a un diabético, se establece que la dosis del mismo, expresada en mg, está en función del peso del paciente según la gráfica: a) ¿Qué dosis corresponde a los siguientes pesos? 50 kg, 40 kg, 70 kg. b) ¿A qué peso corresponde la máxima dosis?. c) ¿Se puede administrar administrar a bebés? d) ¿Y a personas obesas?. c) ¿Qué peso tenía una persona a la que suministraron 40 mg? CRECIMIENTO Y DECRECIMIENTO. MÁXIMOS Y MÍNIMOS Una función es creciente cuando al aumentar la X, también aumenta la Y. Una función es decreciente cuando al aumentar la X, la Y disminuye. Si al aumentar la X la Y se mantiene en un mismo valor, entonces la función es constante. constante Un máximo es un punto donde la función pasa de ser creciente a decreciente, y un mínimo es un punto donde la función pasa de ser decreciente a creciente. Ejercicios. 5. Indica las zonas de crecimiento y decrecimiento en esta función. Indica los máximos y lo loss mínimos. FUNCIONES DADAS POR TABLAS DE VALORES Cuando de una función solo conocemos los valores podemos pasarlos a una gráfica para interpretarlos con más claridad. Veamos algunos ejemplos: El ordenador incorporado al equipo de un globo aerostático ha ido anotando las lecturas del altímetro durante una ascensión recreativa: a) Representa la gráfica de la altura del globo en función del tiempo. b) ¿Cuánto tiempo duró el vuelo? c) ¿Cuánto tardó el globo en alcanzar la altura máxima? d) ¿Cuál fue la altura máxima alcanzada? e) ¿Cuánto duró el descenso? Ejercicios. 6. Un deportista preocupado por su peso ha hecho una anotación mensual del mismo, el último día de Cada mes, a lo largo de un año: Dibuja la gráfica de la función que relaciona el peso con los meses del año. CONSTRUCCIÓN DE LA TABLA DE VALORES Para realizar la tabla de valores hemos de conocer la expresión algebraica de la función. Se trata de ir dándole valores a la X y sustituirlos en la función para calcular la Y La expresión algebraica no es más que la relación matemática entre la X y la Y Por ejemplo, dada la función y = 2x+3 X -3 -2 -1 0 1 2 3 4 y Ejercicios. 7. Representa la función y = X x+2 2 8. Representa la función y =x2 -6x + 3 0 2 4 6 8 2 4 6 8 10 10 y X y 0 12 12 FUNCIONES DE PROPORCIONALIDAD: y = mx Este tipo de funciones se representan mediante una recta y siempre pasan por el punto (0,0) La m es la pendiente y nos da información sobre la inclinación de la recta. Veamos un ejemplo de este tipo de funciones. En un parque hay una tienda donde alquilan patines a 0,5 € la hora y bicicletas a 2 € la hora. Veamos la función que nos da el coste de los patines en función del tiempo Tiempo (h) 0 1 2 3 4 ….. x Coste (€) Veamos la función que nos da el coste de la bicicleta en función del tiempo Tiempo (h) Coste (€) 0 1 2 3 4 ….. x Ejercicios. 9. Representa gráficamente las siguientes rectas: a) y = −2 x b) y = 2 x 3 10. Halla la expresión algebraica de las siguientes rectas 11. En cierta ferretería venden rollos de 20 metros de alambre a 3 euros. a) ¿Cuánto cuesta cada metro de alambre? b) Haz una tabla que nos indique el precio de 1, 2, 3, 4, 5, … metros. c) Representa la correspondiente gráfica y comprueba que corresponde a una función lineal. d) Escribe la expresión algebraica de esta función. ¿Cuál es la pendiente? PENDIENTE DE UNA RECTA La pendiente de una recta mide la inclinación de la misma y se representa por m. Si m>0 la recta es creciente. Si m<0 la recta es decreciente. Vamos a calcular las pendientes de estas rectas Ejercicios. 12. Calcula la pendiente de estas rectas. 13. Representa las funciones sin hacer tabla de valores. a) y = x b) y = 2 x 5 c) y = 3 x d) y = − 1 5 x e) y = − x 3 2 FUNCIONES LINEALES: y = m x + n Estas funciones se representan mediante una recta pero no pasan por el punto (0 , 0), 0) sino que cortan al eje Y en el punto (0 , n). A n se le llama ordenada en el origen. Veamos un ejemplo de este tipo de funciones. Un fontanero cobra 10 € por el desplazamiento y 15 € por cada hora de trabajo. Vamos a hacer una tabla de valores Tiempo (h) Coste (€) 0 1 2 3 4 5 Ahora representamos estos valores. La ecuación de esta función será: Y= Ejercicios. 14. Representa las siguientes funciones: a) y = 2 x − 3 b) y = 3 5 x + 4 c) y = − x + 1 2 3 15. Escribe las ecuaciones de estas funciones. 16. Dibuja las siguientes funciones sin hacer tabla de valores. a) y = − 1 x −3 2 b) y = −3 x − 1 c) y = x − 4 17. Un fabricante de ventanas cuadradas cobra a razón de 3 euros por cada metro de marco y 12 euros por el cristal, sean cuales sean las dimensiones. a) ¿Cuánto costará una ventana de 2 metros de lado? b) Por una ventana hemos pagado 60 euros, ¿cuánto mide su lado? c) Encuentra la expresión que nos dé el precio de la ventana en función de las dimensiones y realiza una representación gráfica gráfica de esta función. FUNCIONES CONSTANTES: y = n Su representación gráfica es una recta de pendiente cero (horizontal) y que pasa por el punto (o , n) Ejercicios. 18. Representa las siguientes funciones. a) y = 3 b) y = -4 c) y = 0 19. Escribe la ecuación de las siguientes funciones: EJERCICIOS 1. Dibuja sobre un papel cuadriculado unos ejes coordenados y representa los siguientes puntos: A(3, 2); B(3, 7); C(4, –1); D(–4, 3); E (–6, –2); F (0, 5); G(3, 0); H(–2, 0); I (0, –5); J (0, 0) 2. Di las coordenadas de cada uno de los siguientes puntos: 3. Representa los puntos siguientes: A(0, 2); B(4, 7); C(4, 1); D(1, 0); E(0, 1); F(6, 1); G (6, 0). Une mediante segmentos AB, BC, CA, DE, EF, FG, GD. 4. Completa la tabla con las coordenadas de los puntos representados en la imagen siguiente: 5. Cada punto del diagrama siguiente representa una llamada telefónica: a) ¿Cuál ha sido la llamada más larga? b) ¿Cuál ha sido la llamada más corta? c) Una de las llamadas ha sido a Australia. 6. Uno de los puntos representados es incorrecto. Indica sus coordenadas. 7. ¿Cuáles de las siguientes gráficas corresponden a una función y cuáles no? Explica por qué. 8. Entre las siguientes representaciones gráficas hay una que no corresponde a una función. 9. Indica el dominio, las zonas de crecimiento y decrecimiento así como los máximos y los mínimos si los hay. 10. Representa gráficamente una carrera de 200 m entre dos corredores, con las siguientes características: A sale más rápidamente que B, y en 5 segundos le saca 10 m de ventaja. A se cae en el instante 5 segundos, y B le adelanta. Pero A se levanta en 2 segundos, y adelanta a B en la misma línea de meta. 11. Rafael y María ponen a competir, en una carrera, a sus caracoles; uno de ellos lleva una pegatina roja, y otro, una pegatina verde. El verde tarda en salir y se para antes de llegar. a) ¿Cuánto tiempo está parado en cada caso? ¿A qué distancia de la meta se para definitivamente? b) ¿Cuántos centímetros y durante cuánto tiempo marcha el rojo en dirección contraria? 12. Escribe, a partir de los datos de la gráfica, el nombre del volcán más alto y el nombre del volcán que ha sufrido más erupciones. 13. Marta ha salido a dar un paseo. ¿Cuánto ha durado ese paseo? ¿A qué distancia se encuentra el punto más alejado de su casa? 14. La empresa EDAD S.A. cotiza en Bolsa desde hace algunos años. En la gráfica adjunta se muestran las cotizaciones (en €) de sus acciones durante el año 2008. ¿Qué representa cada eje? ¿Cuál ha sido la mayor cotización alcanzada por sus acciones? ¿En qué mes se consiguió? ¿Cuál ha sido el menor valor alcanzado por las acciones? ¿Cuál fue el mes en que se alcanzó esa mínima cotización? ¿Qué cotización se alcanzó en el mes de junio?: 15. La gráfica describe la velocidad de un bólido de carreras en cada lugar de este circuito: Di en qué tramos la velocidad es creciente y en cuáles es decreciente. ¿A qué crees que se deben los aumentos y las disminuciones de velocidad? Señala el máximo y el mínimo de esta función. 16. Entre las gráficas siguientes, indica la que corresponde la situación: "Un paseante sale de su domicilio, camina durante 3 horas, se para durante una hora, y retorna a su casa en autobús." 17. Un paracaidista se lanza de un avión desde una altura de 3000 metros. Controlamos su altura cada 20 segundos de acuerdo con la siguiente tabla: a) Dibuja la gráfica que relacione la altitud con el tiempo. b) Obtener aproximadamente su altitud a los 50 seg. c) ¿Al cabo de cuántos segundos la altitud será de 1.800 metros? d) ¿A partir de qué altitud y a partir de cuántos segundos la velocidad del paracaídas es constante? 18. Esta gráfica corresponde al porcentaje de personas que ven la televisión o escuchan la radio, en las distintas horas del día. a) Describe la curva correspondiente a la televisión: dónde es creciente, dónde es decreciente, máximos, mínimos… Relaciónala con las actividades cotidianas: levantarse, acostarse, comida, cena… b)Haz lo mismo con la curva correspondiente a la radio. c) Compara las dos curvas y relaciónalas. 19. La gráfica posición-tiempo de una moto es la siguiente: a) ¿Cuál será la posición de la moto transcurrido un tiempo de 2 h? b) ¿Con qué velocidad circula la moto? 20. En las instrucciones de un medicamento, que hay que administrar a un diabético, se establece que la dosis del mismo, expresada en mg, está en función del peso del paciente según la gráfica: a) ¿Qué dosis corresponde a los siguientes pesos? 50 kg, 40 kg, 70 kg. b) ¿A qué peso corresponde la máxima dosis?. ¿Se puede administrar a bebés?¿Y a personas obesas?. c) ¿Qué peso tenía una persona a la que suministraron 40 mg? 21. Representa las siguientes gráficas: a) Altura de una pelota que está botando cada vez menos, hasta que se para. b) La temperatura de un plato de sopa que se queda sobre la mesa, sin consumir. c) La distancia a la Tierra de un satélite artificial que da vueltas y vueltas. d) La altura a la que se encuentra el asiento de un columpio cuando se balancea. 22. Intenta representar en unos ejes de coordenadas la relación entre el espacio recorrido y el tiempo transcurrido del siguiente itinerario: “6 km alejándonos en la primera hora, descanso para el bocadillo: 30 min. Otros 4 km de alejamiento en 30 min y vuelta al punto de partida en 1h.” 23. El otro día salí de casa y estuve paseando, la gráfica de mi paseo es la que aparece a continuación. En el eje horizontal aparece el tiempo en intervalos de 15 minutos y en el vertical la distancia de mi casa en kilómetros. Realiza una gráfica de mi paseo. 24. Un tiovivo acelera durante dos minutos hasta alcanzar una velocidad de 10 km/h. Permanece a esa velocidad durante siete minutos y luego frena durante un minuto hasta pararse. Tras permanecer cinco minutos parado, comienza otra vuelta. Dibuja la gráfica tiempo-velocidad 25. Representa gráficamente las rectas que cumplan estas condiciones: a) Pasa por el origen y tiene de pendiente 2. b) Pasa por el punto P(2,3) y tiene de pendiente 3. c) Tiene de pendiente -2 y su ordenada en el origen es 3. d) Tiene de pendiente +3 y su ordenada en el origen es -2. e) Escribe las ecuaciones de las rectas que has representado. 26. Representa las siguientes funciones dando a x, en cada caso, los valores que se indican: 27. De una familia de rectángulos cuyo perímetro es 20 cm hemos medido su base y su área. Estos son los resultados: a) Representa la función. b) Comprueba que la ecuación de esta función es: y = 10x – x2 28. Se ha medido, mes a mes, la estatura de un niño desde que nace hasta que tiene un año. Estos son los resultados: Representa los resultados en una gráfica. 29. Durante diez semanas seguidas, un lanzador de peso ha anotado su mejor marca obtenida durante sus entrenamientos. La tabla de la derecha recoge los resultados logrados. Representa la función en tu cuaderno. 30. Representa gráficamente la parábola y = x2 - 4x + 3, 3 indicando los puntos de corte con los ejes 31. Halla la pendiente de cada una de las siguientes rectas: 32. Representa las siguientes funciones: 33. Escribe la ecuación de cada una de las siguientes funciones: 34. Representa gráficamente las rectas que cumplan estas condiciones: a) Pasa por el origen y tiene de pendiente 2. b) Pasa por el punto P(2,3) y tiene de pendiente 3. c) Tiene de pendiente -2 y su ordenada en el origen es 3. d) Tiene de pendiente +3 y su ordenada en el origen es -2. e) Escribe las ecuaciones de las rectas que has representado. 35. ¿Pertenece el punto que tiene por coordenadas (-3,1) a la gráfica de la función y = 3x? 36. Margarita pasea alejándose de su pueblo a una velocidad de 2 km/h. En este momento se encuentra a 4 km del pueblo. a) ¿Dónde se encontrará dentro de una hora? b) ¿Dónde se encontraba hace una hora? c) Representa su distancia al pueblo en función del tiempo transcurrido a partir de ahora. d) Halla la ecuación de la función llamando x al tiempo e y a la distancia al pueblo. Sol: a) A 6 km del pueblo. b) A 2 km del pueblo. d) y = 2x + 4 37. Queremos comprar unos libros en Internet, el precio de cada ejemplar es de 2 € y los gastos de envío son de 3 €. Realiza una tabla con el importe de diferentes compras. Representa los resultados con una gráfica y deduce cuál será la expresión que representan esos puntos. 38. Tenemos un rebaño de ovejas y queremos representar la relación que hay entre el número de cabezas y el de patas. Para ello, hacemos una tabla y después representamos los puntos de esa tabla sobre unos ejes de coordenadas. Haz tú la tabla y representa los puntos. Encuentra una expresión que relacione las coordenadas de esos puntos. 39. Si cada paso que doy mide 70 cm, encuentra una relación entre los pasos y la distancia que recorro. 40. Con los datos de la gráfica calcula a cuánto se ha vendido el kilo de fruta. 41. Con un hilo de 20 cm cuyos extremos están atados entre sí formamos rectángulos a) Razona que la relación entre su base, x, y su altura, y, es y = 10 – x b) Representa la gráfica de la función. c) Si multiplicamos la base, x, por la altura, 10 – x, obtenemos el área: A = x (10 – x). Completa en tu cuaderno la tabla de valores y comprueba que es la misma que la del ejercicio 12. 42. En una cierta compañía de teléfonos móviles, la tarifa para llamadas a países de la U.E. es 1 € por establecimiento de llamada y 0,50 € por minuto de conversación. a) Pon la ecuación de la función que relaciona el coste en euros ( y) en función de la duración de la llamada en minutos (x). b)Representa la gráfica de la función.. Sol: a) y = 0,5x + 1 43. En las 10 primeras semanas de cultivo de una planta, que medía 2 cm, se ha observado que su crecimiento es directamente proporcional al tiempo, viendo que en la primera semana ha pasado a medir 2.5 cm. Establecer una función a fin que dé la altura de la planta en función del tiempo y representar gráficamente. 44. La cuota de abono mensual de Telefónica es de 9,6 euros y cada paso cuesta 0,03 euros. Encuentra la ecuación que permita calcular el gasto del teléfono y represéntala gráficamente. 45. En la copistería del instituto, hacer una fotocopia tiene un coste de 0,10 €. a) Elabora una tabla donde se muestre el coste de hacer 1, 2, 3, 4, ….. , 10 fotocopias. b) Representa esos valores de la gráfica c) Halla la ecuación de la función d) ¿Cuál es la pendiente de dicha función? e) ¿Qué significado tiene el valor de dicha pendiente? 46. El recorrido de un taxi tiene un precio fijo de 3 € más 0,25 € por cada kilómetro recorrido. a) Construye una tabla de valores de la función (kilómetros-euros) y haz la representación gráfica a partir de dicha tabla. b) Halla la ecuación de la función. c) Indica la pendiente de dicha función d) Si me han cobrado 5,5 €, ¿cuántos kilómetros ha recorrido el taxi? 47. En un aparcamiento nos ofrecen las siguientes opciones: a) 10 € por hacerse socio y 1 € por cada hora que aparquemos b) 2 € por cada hora Estudia cuál de las dos opciones es más económica AUTOEVALUACIÓN 1. Dibuja una gráfica que no corresponda a una función. 2. Representa gráficamente las siguientes rectas. En los apartados a y c indica cuánto vale la pendiente y la ordenada en el origen a) y = 2 − 2 x b) x = −5 c) y= 3x −1 2 d) y = 3 3. Escribe las coordenadas de los puntos y sitúa en el eje de coordenadas de la derecha los puntos A = (-3; 4), B = (0;-2), C=(-2; -3) y D=(4;0) 4. Indica el lago de mayor extensión y el lago que se encuentra a mayor altura. 5. Asocia cada función a su gráfica: a) y = −1 b) y = x − 2 c) y= 2 x +1 5 d) y= 5 x +1 2 6. Un depósito se llena mediante una bomba que vierte 74 litros de agua por minuto. ¿Cuál de las tres rectas representa el agua del depósito en función del tiempo? 7. La siguiente gráfica corresponde al recorrido que sigue Antonio para ir desde su casa al trabajo: • ¿A qué distancia de su casa se encuentra su lugar de trabajo? • ¿Cuánto tarda en llegar? • Ha hecho una parada para recoger a su compañera de trabajo, 8. Dibuja las gráficas siguientes sin hacer tablas de valores: a) y = 2 x 3 b) y = −3 x + 4 9. Completa la tabla de valores para la función y = x2 – 4x c ) y = −3 y dibuja su gràfica. x y −1 −5 0 1 2 3 4 5 10. Escribe la pendiente y la ordenada en el origen de las siguientes rectas: a) y = 2 x−6 5 b) y = 3 + 5 x c) y = 6 d) y = x 11. Cuando se excava hacia el interior de la tierra, la temperatura aumenta con arreglo a la siguiente fórmula: t = 15 + 0,01 . h Donde t es la temperatura alcanzada en grados centígrados y h es la profundidad, en metros, desde la corteza terrestre. Calcular: • ¿Qué temperatura se alcanza a los 100 m de profundidad? • ¿Cuántos metros hay que excavar para alcanzar una temperatura de 100 ºC? 12. Por el alquiler de un coche cobran 100 € diarios más 0.30 € por kilómetro. Encuentra la ecuación de la recta que relaciona el coste diario con el número de kilómetros y represéntala. Si en un día se ha hecho un total de 300 km, ¿qué importe debemos abonar? 13. Una compañía telefónica cobra, en las llamadas internacionales, 20 céntimos por el establecimiento de llamada y 10 céntimos el minuto. Escribe la ecuación que relaciona el tiempo que dura un llamada (x) con el coste de la misma (y) y represéntala. 14. Pedro va a comprar naranjas al precio de 3 euros/kg. Escribe la ecuación que relaciona la cantidad comprada (x) con el dinero abonado (y) y represéntala.