Chuleta Integrales
Anuncio

t ~
k ·><
~
f\ x
+e
/
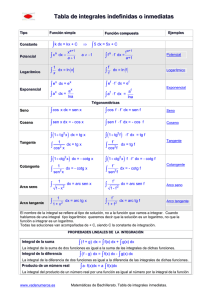
INTEGRALES INMEDIATAS
~
TIPOS
SIMPLES
COMPUESTAS
Tipo
potencial
Ck* -1)
xk+l
Jxkdx= --+ e
k+l
f[J(x)t ·f'(x)dx= [f(x)]k+l +e
k+l
Tipo raíz
cuadrada
f--dx=,)
1
x+e
J j' (X)
Tipo
logaritmico
I_!..X dx = In lxl + e
r-
2Fx
2~)
dx =
Jj (X) +e
1
ax
Jaxdx=-+e
lna
Jf'(x)·af(x)dx=-a-+e
Tipo seno
fCOS Xdx = sen.x +e
Jf'(x)·cosf(x)dx == senf(x)+e
Tipo
coseno
Jsenxdx = -cosx+ e
f f'(x). senf(x)dx = -cos f(x)+ e
Tipo
tangente
fSCC
dx = tgx +e
Jf'(x)·sec 2 f(x)dx=tgf(x)+C
2
Jf'(x)(l +tg 2 f(x))dx = tgf(x)+e
1---·
2
X
f(} + tg
X) dx = tg X + e
Tipo
cotan gente
\
Tipo arco
coseno
Tipo arco
tangente-
In a
J
Jcosec2x dx = - cotg x + e
I rcx) ·cosec2 f(x)dx = -cotgf(x) +e
f'(x) dx = tg f(x)+e
cos 2 f(x)
J(1+ COtg 2X) dx = - COtg X + e ff'(x)(l+cotg 2f(x))dx=-cotgf(x)+e
I-sen1-·x dx = - cotg X+ e
J
Jhdx=arcsenx+e
2
JJ f'(x)
J~dx
-1
= arCCOS X+ e
JJ -f(x)
2
Tipo arco
seno
f(x)
1
f-dx = tgx +e
COS X
-2
..
f(x)
I f'(x)· ef(x)dx = ef(x) +e
'
\
Jf'(x) dx=Inlf(x)l+e
Iexdx=ex +e
Exponencial
\
1
1-x
X
1
Jl+x
2
dx = arctgx+e
f:(x) dx = -cotgf(x)+e
sen f(x)
eh;~ arcsenf(x)+C
l - [f(x)t
eh;~ arccosf(x)+C
1-[f(x)Y
f
f' (X) 2 dx = arctg j (X) + e
l+[f(x)]
¡-;:;- .._
VX n
_ ._
~(x)
-
rv .d
\\ c~ij
V.::: V.
)e
V
-s
d-er.' ve.,.
-~)
d v::
V •
lQ(x)
e ex)
dV ~ u\'\
cl(t.'\ v/
V\'\•'{. V' W\"€
VI'\
\1 0\.
1.' -e~ h
S'd 1 de..J e
V "t'Sj.,
1
do
el t.'
MATEMÁTICAS 1- INTEGRALES Y PROBLEMAS DE OPTIMIZACIÓN
1.- Calcula las siguientes integrales indefinidas:
a)
f-5- dx
3x-2
b)
f---7-dx
x- +5
e)
d)
f~
e)
f~dx
X+)
ff7x+2dx
x- + 25
g}
J1+.) 9x dx
h}
f32x+ldx
i)
j)
f
se~
dx
X
k)
f
f-/7 + 2tgx dx
cos- x
n)
Jsxcos(x 2 +3)dx
ñ)~
J~+V dx
p)
J5x-7 dx
x3
q)
xlnx
-, x
COS
m)
o)
J
J
x-
1
(x+5)
2dx
)
1)
J+
x- +5 dx
J
J ~' dx
e
f ~:2x_I dx
f 7x
X +2
ftg; dx
2.- Halla las dimensiones de una cartulina rectangular de perímetro 60 cm . que, al dar una
vuelta completa alrededor de un lado vertical, genera un cilindro de volumen máximo.
3.- Un artista ha adquirido un listón de 6 metros de largo del que quiere colgar dos grandes
telas rectangulares, una a continuación de la otra y que ocupen todo el listón: la primera ha de
ser naranja, y el lado que está sobre el listón debe ser un tercio del lado que cuelga; y la otra
será verde y debe tener forma de cuadrado. ¿Qué dimensio nes deben tene r las telas para que
su superficie sea la mínima posible?