FUNCIONES TRIGONOMETRICAS Con el programa Funciones
Anuncio

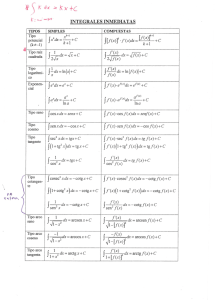
MATEMÁTICA APLICADA TRABAJO PRÁCTICO: FUNCIONES TRIGONOMETRICAS Con el programa Funciones trigonométricas 2.0 puedes graficar las seis funciones (seno, coseno, tangente, cotangente, secante y cosecante). Observar el siguiente ejemplo: FUNCIÓN SENO: y= sen B FUNCIÓN COSENO: y=cos B En el estudio de funciones es muy importante conocer ciertas características de la gráfica de las funciones como las que se detallan en el siguiente cuadro: 1) Completar el cuadro de análisis de las FUNCION COSENO, luego de analizar los datos registrados para la función seno. FUNCIONES Y= sen B Y= cos B Dominio (-∞,∞) Codominio [-1,1] Intersección eje x X1=0; x2= π; x3=2π;… Intersección eje y X= 0 Valor Máximo 1 Valor Mínimo -1 Intervalos de crecimiento (0, π/2) y (3 π/2, 2 π) Intervalos de decrecimiento (π/2, 3 π/2) Período 2π 2) Obtener los valores de la función coseno para los valores angulares dados en la siguiente tabla y graficar en un sistema cartesiano. (Sugerencia: Utilizar calculadora) 0 π/6 π/4 π/3 π/2 3 π/4 5 π/6 π 5 π/4 3 π/2 5 π/3 x Y= cosx y x FUNCIÓN TANGENTE: y= tg B Observar que la gráfica de la función tangente no es continua como la función seno y coseno. Presenta asíntotas verticales en π/2, 3 π/2, 5 π/2,…. es decir en los múltiplos impares de π/2. Además es siempre creciente y su codominio es el conjunto de los números reales (R). 3) Calcular los valores de la tangente: Tg 0= ….. (Recordar que tg x = sen x / cos x) tg π/4 =…… tg π/2= …… Tg π=…… FUNCIÓN COTANGENTE 4) Visualizar el gráfico de la función cotangente obtenido con el programa Funciones trigonométricas 2.0 y responder: a) ¿La gráfica presenta asíntotas verticales? ¿en qué valores del dominio? b) Investiga con la calculadora los valores de: cotg 0= ….. cotg π=….. cotg 2π= …. (Recordar que cotg x= cosx / senx) c) ¿Cuál es el dominio de esta función? Y su codominio? d) ¿Cuál es el período de la función cotangente? CONSULTA LAS DUDAS A TRAVÉS DEL FORO DEL AULA VIRTUAL www.matconso.ecaths.com