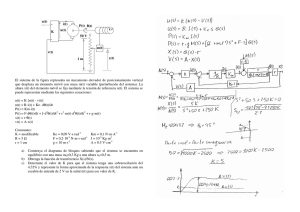
Problemas hoja 1 segundo cuatrimestre

Problemas de Química Física II. 3º de Químicas
MICROONDAS
1. El espectro rotacional del 79Br19F muestra una serie de líneas equiespaciadas en
0.71433 cm-1. Calcular la constante rotacional B y, a partir de ella, el momento de
inercia y la longitud de enlace de la molécula. Determinar el número de ondas para la
transición J=9  J=10 y encontrar qué transición da lugar a la línea más intensa a
temperatura ambiente. Sol: B = 0.3572 cm-1, I = 7.8375x10-46Kg.m2, R = 1.755 Å,
 109 = 7.143 cm-1, Jmax = 17.
2. Se observan tres líneas consecutivas del 79Br1H a 84.544, 101.355 y 118.112 cm-1.
Asignar las transiciones rotacionales correspondientes a cada una la transición J-J'
deduciendo los valores de B y D, y de aquí, la longitud de enlace y la frecuencia de
vibración aproximada de la molécula. Masas atómicas: 79Br= 78.9184 uma, 1H= 1.0078
uma.
Sol: J=4J'=5, J=5J'=6 y J=6J'=7. B=8.473 cm-1; D=3.71x10-4 cm-1; R=1.414
x10-10 m ;  e 2560 cm-1.
3. En el espectro de rotación del 12C16O se observan las siguientes transiciones
consecutivas: 30'8892, 34'7465 y 38'6021 cm-1. Asignar las transiciones empleando
un modelo de rotor rígido. Hallar las constantes rotacionales Be y De, el nivel
rotacional más poblado a 300K y la distancia internuclear de equilibrio.
Sol: J: 7 8; 8- 9 y 9 10. B = 1.931 cm-1, D = 0.00000653 cm-1 , R = 1.128 Å,
nivel más poblado Jmax = 7.
4. En el espectro de microondas del 19F79Br se han medido las siguientes líneas
consecutivas en cm-1: 0.7199, 1.4395, 2.1584, 2.8762, 3.5925, 4.3070, 5.0194,
5.7293, 6.4363, 7.1400, 7.8401. Determinar la longitud de enlace de la molécula de
FBr. Determinar su constante de distorsión centrífuga. Determinar el valor de J para
correspondiente a su máximo de absorción a 300 K. Estimar cuál será la frecuencia
de las tres primeras líneas del espectro de microondas del 19F81Br, suponiendo que su
constante de distorsión centrífuga es la misma que la del 19F79Br. Masas atómicas:
19
F 18.9984; 79Br 79.904; 81Br 80.9932
Sol: B = 0.3583 cm-1, D = 0.0000150 cm-1 , R = 1.749 Å, nivel más poblado Jmax = 16.
Las tres primeras líneas son 0.7165, 1.4323 y 2.1482 cm-1
5. La línea del espectro de microondas del 12C16O correspondiente a la transición
J=0  J=1, en el estado fundamental de vibración, está a 3.84235 cm-1 y la de la
molécula 13C16O a 3.67337 cm-1. Sabiendo que la masa atómica del 16O es 15.9994
uma; Calcular: (a) la longitud del enlace en la molécula 12C16O y (b) la masa atómica
del 13C.
Sol: (a) R = 1.131x10-8 cm, (b) m(13C) = 13.00069 uma.
6. Hallar la relación del número de moléculas de HCl en los niveles J=0 y J=1 sabiendo
que B=10.56 cm-1. Hacer el cálculo a 100 K y 1000 K.
Sol: N1/N0(100 K) = 2.214, N1/N0(1000 K) = 2.910.
7. Las frecuencias del espectro de rotación pura del HF en cm-1 son: 41.13; 82.19;
123.15; 164.00; 204.62; 244.93; 285.01; 324.65; 363.94; 402.82. Calcular las
constantes B y D.
Sol: B = 20.57 cm-1, D = 2.1x10-3 cm-1.
8. A partir de las constantes rotacionales que se dan a continuación, determinar la
longitud del enlace 1H19F, así como los números de onda para las transiciones
rotacionales puras: J=0  J=1, J=1  J=2, J=2  J=3, J=3  J=4, (a) con el
modelo del rotor rígido, (b) con el modelo del rotor no rígido. Be = 20.956 cm-1, e =
0.796 cm-1 y D = 2.2x10-3 cm-1.
Sol: R = 0.9168 Å; (a) 41.116, 82.232, 123.348, 164.464 cm-1; (b) 41.107, 82.162,
123.110, 163.901 cm-1.
9. La constante rotacional del 35Cl1H se observa a 10.5909 cm-1 ¿Qué valor de B tendrán
el 37Cl1H y 35Cl2H? Masas atómicas: 1H= 1.0078 uma, 2H= 2.0141 uma, 35Cl= 34.9689
uma, 37Cl=36.9559 uma.
Sol: B= 10.5739 cm-1 y B= 5.446 cm-1
10. Dada la siguiente tabla para la molécula de 12C16O, donde todas las transiciones
corresponden al nivel vibracional v = 0, (a) calcular Bo y Do para esta molécula; (b) si
la transición J’’= 0  J’= 1 en el estado vibracional v = 1 se produce a una
frecuencia de 114221.2 MHz, calcular Be; (c) calcular la distancia internuclear de
equilibrio Re;.
J’’  J’
0
1
1
2
2
3
3
4
4
5
MHz)
115261.20
230542.97
345812.90
461083.70
576354.82
Sol: Bo = 1.9223 cm-1, Do = 0.000025 cm-1 , B1 = 1.905 cm-1 , Be = 1.9309 cm-1, R =
1.128 Å.
11. Calcular las frecuencias de las tres primeras transiciones del 127I35Cl en MHz y cm-1.
La distancia interatómica es 2.32 Å. Ignorar la distorsión centrífuga. Masa del 127I =
126.9044 uma.
Sol: J(01) 0.228 cm-1 o 6840 MHz, J(12) 0.456 cm-1 o 13680 MHz, J(23) 0.684
cm-1 o 20520 MHz.
12. Calcular B0, , y R0 para la molécula de 127I2H asumiendo el modelo con interacción
rotación-vibración: el rotor no es rígido pero se considera como si lo fuera para cada
nivel v. Datos D = 0.60 MHz, Be = 98446 MHz y la transición de J=0 a J=1 (para v=0)
195067.866 MHz.
Sol: B0 = 97535.14 MHz, = 1822 MHz y R0 = 1.617 Å.
13. En el espectro de rotación de la molécula de CO se obtuvieron las siguientes líneas
3.845033, 7.689919, 11.534509, 15.378662, 19.222223 y 23.065043 cm-1. Determinar
B y D en cm-1.
Sol: B = 1.92250 cm-1 y D = 5.966x10-6 cm-1.
14. Las constantes rotacionales para el 12C16O son 1.9314 cm-1 y 1.6116 cm-1 en v=0 y v=1
respectivamente. ¿Cuánto cambia la longitud del enlace al pasar del estado fundamental
al excitado?
Sol: R1 = 1.0947 R0 .
15. Para medir la temperatura de un cuerpo celeste que contiene 12C16O se recurre a la
espectroscopia de microondas. Cuando se obtiene dicho espectro en el laboratorio a
300K se encuentra que el pico más intenso corresponde a la transición J: 7 → 8 y le
sigue en intensidad el de J: 6 → 7. Además, el cociente de ambas intensidades es
1.0135. Cuando se analiza el espectro del cuerpo celeste se encuentra que la
transición más intensa corresponde a J: 3 → 4 seguida de la J: 2 → 3 y su relación de
intensidades es 1.0029. Se pide: a) calcular la constante rotacional del 12C16O y b)
estimar la temperatura del cuerpo celeste.
Sol: B = 1.93 cm-1,aprox, T = 50 K aprox..
16. En unas condiciones adecuadas para que los siguientes sistemas sean gaseosos, y
suponiendo equilibrio térmico en éstos sistemas, a) Ordena de mayor a menor valor
de la constante rotacional B. b) ¿Para cuál de los siguientes sistemas habrá una mayor
proporción de moléculas en niveles rotacionales excitados? c) Ordena de mayor a
menor separación entre las líneas del espectro de microondas.
7
Li2, 19F2, 1H19F, 1H7Li y 7Li19F.
Datos de Re (Angstrom): Li2 = 2'67 ; HLi = 1'59 ; F2 = 1'41 ; HF = 0'92 ; LiF= 1'56.
En las mismas condiciones anteriores, ¿Cuál de dichas moléculas presentará un mayor
número de líneas apreciables en el espectro de microondas realizado a la misma
temperatura?
Nota: Na = 6.0221 .1023 mol-1; h= 6.6261 10-34 J.s; c = 2.9979 108 m/s ; 1 Cal = 4'184 J
; 1 oC = 273.15 K ; R = 8'3144 J/(K mol) ; 1 eV = 1.6022 10-19 J ; 1 Angstrom = 10-10 m
; 0 oC = 273.15 K ; kB = 1'3807.10-23 J/K. m (1H) = 1.0078 uma; m (2H) = 2.0141 uma;
m(16O) = 15.99491 uma; m (17O) = 16.9991 uma; m (12C) = 12.0000 uma; m (13C) =
13.0034 uma, m (14N) = 14.0031 uma. ; m(39K) = 38.9637 uma ; m(7Li) = 7.0160 uma ;
m (19F) 18.9984 uma; m(79Br) = 78.9183 uma; m(81Br) = 80.9163 uma.
Advertencia: Según el número de cifras significativas, los redondeos efectuados
por el alumno y la forma como su calculadora de mano o su ordenador personal
realicen los ajustes por mínimos cuadrados, los resultados que obtenga el alumno
pueden variar ligeramente respecto a los indicados. Se aconseja emplear la mayor
precisión posible y solo redondear los resultados finales, nunca los intermédios, a
lãs cifras significativas adecuadas.