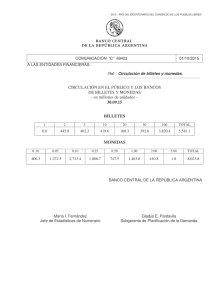
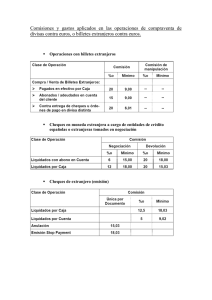
λ x+y+z=1 x+λ y+z=λ x+y+λ z=λ 2 1 2 λ λ −1). Se pide:
Anuncio

PRUEBA TIPO SELECTIVIDAD NUM 3 Se elegirá el ejercicio A o el ejercicio B, del que se harán los TRES problemas propuestos. LOS TRES PROBLEMAS PUNTÚAN POR IGUAL. Cada estudiante podrá disponer de una calculadora científica o gráfica para la realización del examen. Se prohíbe su utilización indebida (para guardar fórmulas en memoria). OPCIÓN A A1. Si A=(C1, C2, C3) es una matriz de orden 3 con columnas C 1, C2 y C3 y se sabe que det(A) = 4, se pide: a) Calcular det(A3) y det (3A). (4 puntos) b) Calcular det (B) y det(B–1 , siendo B= ( 2·C3, C1–C2 , 5C1) la matriz cuyas columnas son 2·C 3, C1–C2 y 5C1. (6 puntos) A2. Discutir y resolver el siguiente sistema, según los distintos valores del parámetro λ. λ x +y +z=1 x +λ y +z=λ x+y +λ z=λ 2 } (10 puntos) A3. Los planos Π: x + y + z = 4; Π': x – z =0 y Π'': x + y =3 tienen un único punto en común. Se pide: a) Determinarlo. (3 puntos) b) Hallar las ecuaciones de las rectas en que cada uno de esos planos corta a x=0. (3puntos) c) Volumen del tetraedro limitado por esos tres planos y el plano x=0. (4 puntos) OPCIÓN B ( ) 4 3 λ B1. Para cada número real λ, M( λ) es la matriz M (λ)= 2 1 2 λ λ −1 . Se pide: a) Obtener el determinante de la matriz M( λ) y justificar que para cualquier valor λ existe la matriz M( λ)– 1 inversa de M( λ) (3 puntos). b) Calcular M( 0)– 1 . (3 puntos). c) Si A= M( 8), B= M(4) y C= M(3), calcúlese, razonadamente, el determinante de la matriz producto A · B– 1 · C– 1 . (4 puntos). B2. El cajero automático de una determinada entidad bancaria sólo admite billetes de 50, de 20 y de 10 €. Los viernes depositan en el cajero 225 billetes por un importe de 7 000€. Averiguar el número d billetes de cada valor depositado, sabiendo que la suma del número de billetes de 50 y de 10€ es el doble que el número de billetes de 20€. (10 puntos) B3. Dados el plano Π: 3x + 2y – z +10 = 0 y el punto P(1, 2, 3), se pide: a) Ecuación de la recta r perpendicular al plano Π que pasa por el punto P. (2.5 puntos) b) Hallar el punto Q intersección de Π y r. (2.5 puntos) c) Hallar el punto R intersección de Π con el eje OY. (2.5 puntos) d) Hallar el área del triángulo PQR. (2.5 puntos)