apendice B - formula..

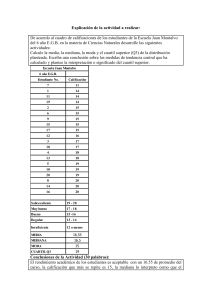
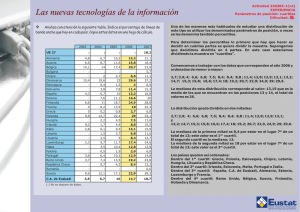
Anexo B
Hoja de Fórmulas de Referencia
Media
A partir de los datos individuales: media = x =
∑x
i
n
Media Geométrica
La media geométrica es la media de una serie de datos, medida en una
1
escala logarímica. Media geométrica = Xgeo = antilog ( ∑ Log xi )
n
Mediana
Identificación de la mediana a partir de los datos individuales:
1. Situar las observaciones en orden creciente o decreciente
2. Hallar el rango medio a través de la siguiente fórmula:
Rango mediano = (n + 1) / 2
a. Si el número de observaciones (n) es impar, el rango mediano coincidirá
con una observación.
b. Si n es par, el rango medio caerá entre dos observaciones.
3. Identificar el valor de la mediana:
a. Si el rango medio cae en una observación concreta (esto es, si n es impar),
la mediana es igual al valor de esa observación.
b. Si el rango medio cae entre dos observaciones (esto es, si n es par) la
mediana es igual a la media (es decir, la media aritmética) de los valores de
ambas observaciones.
Identificación de la mediana para una distribución de frecuencias:
1. Identificar el rango medio de los datos como en el paso # 2 descrito más arriba.
2. Comenzando por el primer valor (puestos en una fila o serie), añadir las frecuencias
de forma acumulativa. Parar cuando la frecuencia acumulativa iguale o exceda el
rango medio.
3. Identificar la mediana como el valor del rango medio.
a. Si el rango medio coincide en un valor determinado de la serie, la mediana
es igual a ese valor.
b. Si el rango medio cae entre dos valores (puestos enla fila), la mediana se
calcula como la media de los dos valores entre los que se encuentra el rango
medio.
Moda
1. Ordenar los datos según una distribución de frecuencias, mostrando los
valores de la variable (xi)y la frecuencia (fi) con la que aparece cada valor.
2. Identificar el valor que aparece con mayor frecuencia.
463
Rango medio Fórmula para calcular el rango medio de una serie de observaciones:
Rango medio (la mayoría de los tipos de datos) = (X1 + Xn)
2
Rango medio (datos de edad) = (X1 + Xn + 1)
2
1. Situar las observaciones en orden creciente de sus valores.
2. Identificar el menor y el mayor valor.
3. Calcular el rango medio con la fórmula que corresponda.
Rango 1. Ordenar los datos en una distribución de frecuencias.
2. Identificar los valores mínimo y máximo.
3. Calcular el rango. Rango = máximo - mínimo
Rango intercuartilar
1. Situar las observaciones en orden creciente.
2. Hallar la posición del primer y tercer cuartiles.
Posición del 1º cuartil (Q1) = ( n +1)
4
Posición del 3º cuartil (Q3) =3(n + 1)
2
3. Identificar el valor del 1º y 3º cuartiles
• Si un cuartil coincide con una observación (esto es, si su posición
es un número completo), el valor del cuartil es el valor de esa
observación.
• Si un cuartil cae entre dos observaciones, el valor del cuartil es el
valor de la observación menor, mas la fracción especificada de la
diferencia entre las observaciones.
4. Calcular el rango intercuartílico como Q3 menos Q1.
Varianza La varianza calculada a partir de los datos individuales es:
2
n∑ xi − (∑ xi ) 2
Varianza = s =
n(n − 1)
Desviación estándar Se calcula a partir de datos individuales
2
2
s=
n∑ xi − ( ∑ xi ) 2
n(n − 1)
Error estándar de la media Error estándar de la media = EEx =
s
s
Límites de confianza
Estas fórmulas se usan para tamaños de muestra de al menos 30.
Límite de confianza inferior, al 95% = media - (1.96 • SE)
Límite de confianza superior, al 95% = media + (1.96 • SE)
= (letra griega Sigma) = suma de
n = el número de observaciones
xi = observación número i (x1 = 1ª observación,
x4 = 4ª observación)
464
fi = frecuencia de xi
x1 = el valor más bajo de la serie
xn = el valor más alto de la serie