2302UDv2 Nuevas Tecnologias c
Anuncio

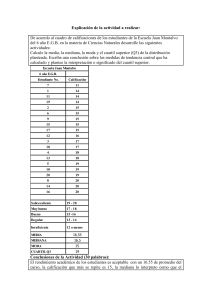
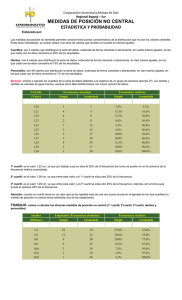
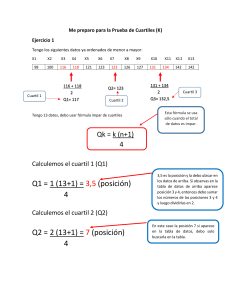
Las nuevas tecnologías de la información v Analiza con atención la siguiente tabla. Indica el porcentaje de líneas de banda ancha que hay en cada país. Copia estos datos en una hoja de cálculo. 2003 UE 27 2004 : 2005 : 2006 : 2007 : 18,2 Alemania 4,8 6,7 10,2 15,3 21,1 Austria 6,6 8,7 11,6 15,8 18,4 Bélgica 10,1 14 17,4 20,7 23,9 Bulgaria : : : : 5,7 Chipre : 2 2,7 6,6 11,1 Dinamarca 10,4 15,6 22 29,6 37,2 Eslovaquia : 0,4 1,5 4 6,9 Eslovenia : 3,8 7,8 11,4 15,3 4,3 6,7 10 13,2 16,8 España Estonia : 7,6 11,1 16,6 20 6,6 11 18,7 24,9 28,8 Francia 4 8,2 13,9 18 22,3 Grecia 0 0,2 0,8 2,7 6,8 Holanda 9,8 14,7 22,4 29 33,1 Hungría : 2,2 4,5 7,5 11,6 15,5 Finlandia Irlanda 0,2 1,7 4,4 8,8 Italia 2,8 6,1 9,5 13,1 15,9 : 1,5 3,7 6,8 11,6 Letonia Lituania : 2,5 5 8,4 12,7 2,3 5,7 11,7 17,4 24,6 Malta : 3,5 10,4 12,8 13,9 Polonia : 0,5 1,9 3,9 6,8 Portugal 3,6 6,4 10,1 12,9 14,8 Reino Unido Luxemburgo 3,7 7,4 13,5 19,2 23,8 República Checa : 0,7 4,3 8,4 12,2 Rumanía : : : : 6,6 Suecia 8,6 12,1 17,1 22,9 28,3 C.A. de Euskadi 3,8 6,7 10 14,7 18,7 (:) No se dispone de datos. Actividad 230205-1(v2) EXPERIENCIA Parámetros de posición: cuartiles Dificultad: . Una de las maneras más habituales de estudiar una distribución de este tipo es utilizar los denominados parámetros de posición, a veces se les denomina también percentiles. Para determinar los percentiles lo primero que hay que hacer es decidir en cuántas partes se quiere dividir la muestra. Supongamos que decidimos dividirla en 4 partes. En este caso estaríamos dividiendo la muestra en “cuartiles”. Comencemos a trabajar con los datos que corresponden al año 2006 y ordenados de menor a mayor: 2,7; 3,9; 4; 6,6; 6,8; 7,5; 8,4; 8,4; 8,8 ; 11,4; 12,8; 12,9; 13,1; 13,2; 14,7; 15,3; 15,8; 16,6; 17,4; 18; 19,2; 20,7; 22,9; 24,9; 29; 29,6. La mediana de esta distribución corresponde al valor: 13,15 que es la media de los que se encuentran en las posiciones 13 y 14, el total de valores es 26. La distribución queda dividida en dos mitades: 2,7; 3,9; 4; 6,6; 6,8; 7,5; 8,4; 8,4; 8,8 ; 11,4; 12,8; 12,9; 13,1; y 13,2; 14,7; 15,3; 15,8; 16,6; 17,4; 18; 19,2; 20,7; 22,9, 24,9; 29; 29,6. La mediana de la primera mitad es 8,4 por estar en el lugar 7º de un total de 13; este valor es el 1er cuartil. El segundo cuartil es la mediana: 13. La mediana de la segunda mitad es 18 por estar en el lugar 7º de un total de 13; este valor es el 3er cuartil. Los países quedan así ordenados: Dentro del 1er cuartil: Grecia, Polonia, Eslovaquia, Chipre, Letonia, Hungría, Lituania y República Checa. Dentro del 2º cuartil: Irlanda, Eslovenia, Malta, Portugal e Italia. Dentro del 3er cuartil: España, C.A. de Euskadi, Alemania, Estonia, Luxemburgo y Francia. Dentro del 4º cuartil: Reino Unido, Bélgica, Suecia, Finlandia, Holanda y Dinamarca. EUSKAL ESTATISTIKA ERAKUNDEA INSTITUTO VASCO DE ESTADÍSTICA Las nuevas tecnologías de la información v Actividad 230205-2(v2) EXPERIENCIA Parámetros de posición: cuartiles Dificultad: . v Haz el mismo trabajo, y define cuartiles y ordena los países con los datos que correspondan al año 2007. Investiga cómo puedes usar las funciones estadísticas de la hoja de cálculo para hacer estos cálculos rápidamente. Haz un estudio comparativo e indica qué países mejoran y cuáles empeoran su posición entre los años 2006 y 2007. ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... ............................................................................... EUSKAL ESTATISTIKA ERAKUNDEA INSTITUTO VASCO DE ESTADÍSTICA