Dispone de 40 minutos
Anuncio
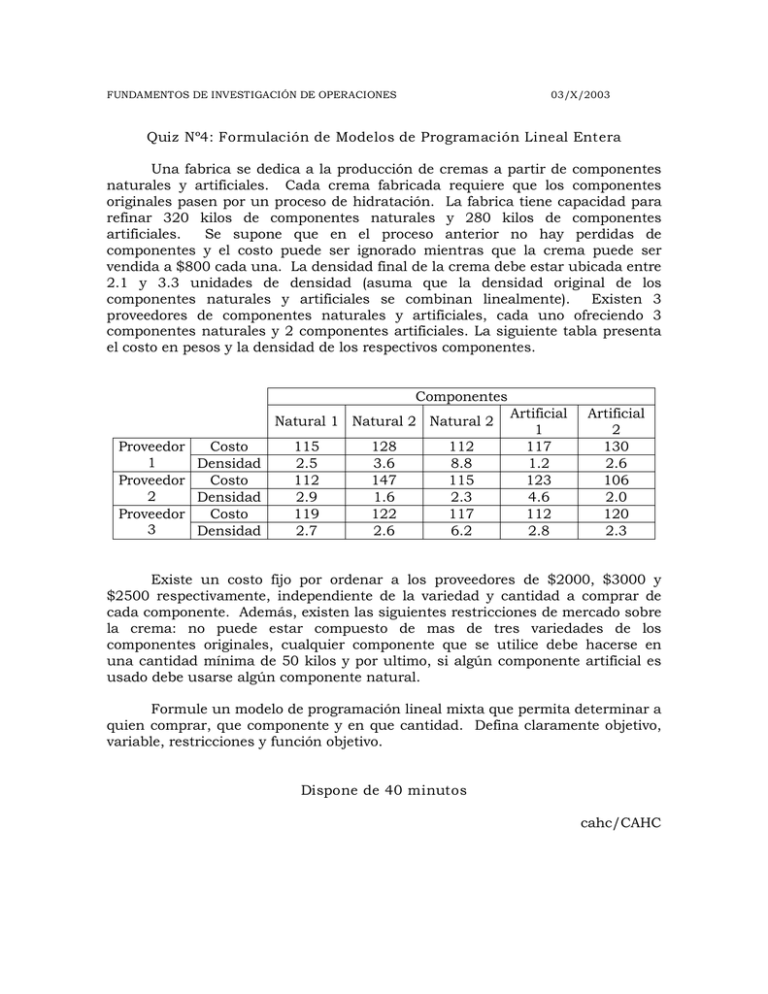
FUNDAMENTOS DE INVESTIGACIÓN DE OPERACIONES 03/X/2003 Quiz Nº4: Formulación de Modelos de Programación Lineal Entera Una fabrica se dedica a la producción de cremas a partir de componentes naturales y artificiales. Cada crema fabricada requiere que los componentes originales pasen por un proceso de hidratación. La fabrica tiene capacidad para refinar 320 kilos de componentes naturales y 280 kilos de componentes artificiales. Se supone que en el proceso anterior no hay perdidas de componentes y el costo puede ser ignorado mientras que la crema puede ser vendida a $800 cada una. La densidad final de la crema debe estar ubicada entre 2.1 y 3.3 unidades de densidad (asuma que la densidad original de los componentes naturales y artificiales se combinan linealmente). Existen 3 proveedores de componentes naturales y artificiales, cada uno ofreciendo 3 componentes naturales y 2 componentes artificiales. La siguiente tabla presenta el costo en pesos y la densidad de los respectivos componentes. Componentes Natural 1 Natural 2 Natural 2 Proveedor Costo 1 Densidad Proveedor Costo 2 Densidad Proveedor Costo 3 Densidad 115 2.5 112 2.9 119 2.7 128 3.6 147 1.6 122 2.6 112 8.8 115 2.3 117 6.2 Artificial 1 117 1.2 123 4.6 112 2.8 Artificial 2 130 2.6 106 2.0 120 2.3 Existe un costo fijo por ordenar a los proveedores de $2000, $3000 y $2500 respectivamente, independiente de la variedad y cantidad a comprar de cada componente. Además, existen las siguientes restricciones de mercado sobre la crema: no puede estar compuesto de mas de tres variedades de los componentes originales, cualquier componente que se utilice debe hacerse en una cantidad mínima de 50 kilos y por ultimo, si algún componente artificial es usado debe usarse algún componente natural. Formule un modelo de programación lineal mixta que permita determinar a quien comprar, que componente y en que cantidad. Defina claramente objetivo, variable, restricciones y función objetivo. Dispone de 40 minutos cahc/CAHC Pauta: Objetivo : Maximizar utilidades Variables Xij Yij Zj Wi : Cantidad de componente “i” comprada al proveedor “j”. i=1..5, j=1..3 : 1 si se compra componente “i” al proveedor “j” 0 si no : 1 si se compra al proveedor “j” 0 si no : 1 si se compra componente “i” 0 si no Restricciones Hidratación X11+X12+X13+X21+X22+X23+X31+X32+X33<=320 X41+X42+X43+X51+X52+X53<=280 Densidad 2.5X11+3.6X21+8.8X31+1.2X41+2.6X51+2.9X12+1.6X22+2.3X32+4.6X42 5 +2.0X52+2.7X13+2.6X23+6.2X33+2.8X43+2.3X53>=3.3 3 ∑∑ Xij i =1 j =1 2.5X11+3.6X21+8.8X31+1.2X41+2.6X51+2.9X12+1.6X22+2.3X32+4.6X42 5 +2.0X52+2.7X13+2.6X23+6.2X33+2.8X43+2.3X53<=2.1 3 ∑∑ i =1 j =1 Activación de Variables Xij <= M*Yij Si se compra a cada proveedor 5 ∑ Yij <= 5*Zj j=1..3 i =1 Mínimo a comprar Xij >= 50*Yij i=1..5 j=1..3 Xij Utilización componente tipo “i” 3 ∑ Xij <= 2*Wi i=1..5 j =1 Cantidad máxima de componentes originales 5 ∑ Wi <= 3 i =1 Usar algún componente natural si se usa algún componente artificial W4 <= W1+W2+W3 W5 <= W1+W2+W3 Valor de las variables Xij >= 0 Yij, Zj, Wi Binarias Función Objetivo 5 Max 800 3 ∑∑ Xij – 2000Z1 – 3000Z2 – 2500Z3 – 115X11 – 128X21 – 112X31– i =1 j =1 117X41– 130X51– 112X12– 147X22– 115X32– 123X42– 106X52 –119X13– 122X23– 117X33– 112X43– 120X53











