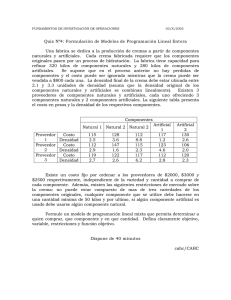
Taller Análisis de Datos Multinivel

Taller
Análisis de Datos Multinivel
Sergio R. Muñoz, Ph.D.
CIGES & Departamento Salud Publica
Facultad de Medicina
Universidad de La Frontera
munozs@ufro.cl
12-25 de Mayo, 2012
Ejemplos
• Datos
– Pacientes en clínicas
– Familias en vecindarios
– Individuos en familias en vecindarios
• Estructura jerárquica o anidada
– Niveles
• Inferencia
– Pérdida de independencia
– Ignorar jerarquía  Consecuencias segun sea la
pregunta a responder
Se desea determinar si la adherencia a un
programa de salud depende de los años de
educación formal de las personas
• Evaluaciónón a nivel de:
– Individuos (2000)
– Familias (600)
– Comunidades (12)
• Análisis: en que nivel?
• Análisis estadístico tradicional focalizado en
un nivel
• Comunidades
– Datos: Promedio de años de educación y
porcentaje de adherencia al programa para
cada comunidad.
– Regresión con 12 observaciones
– Pérdida de información
• Familias
– Datos: Promedio de años de educación y
porcentaje de adherencia al programa para
cada familia
– Regresión con 600 datos
– La variación entre comunidades puede ser
modelada incorporando términos para cada
comunidad
– Pérdida de información
– Procedimiento de estimación ineficiente
(incorpora muchos parámetros en el modelo,
IA)
• Individuos
– Datos individuales de años de educación y de
adherencia al programa
– Regresión con 2000 datos
– La variación entre familias puede ser modelada
incorporando términos para cada comunidad.
Alternativamente puede pensarse en ajustar por
efecto de diseño si se piensa en que la muestra fue por
conglomerados
– La variación entre comunidades puede ser modelada
incorporando términos para cada comunidad
– No hay pérdida de información
– Procedimiento de estimación ineficiente (incorpora
demasiados parámetros en el modelo, IA)
Definición de Niveles y Análisis Estadístico
• Macro niveles
• Micro niveles
• Factores
composicionales
(individuales)
• Factores de Contexto
(grupales)
• Modelos Multinivel
• Modelos de efectos
aleatorios
• Modelos de coeficientes
aleatorios
• Modelos jerárquicos
• Modelos de componentes
de varianza
• Inferencia acerca de la
variación entre contextos
en la población usando
una muestra al azar de
contextos
Análisis Multinivel
• Permite estudiar el efecto simultáneo de
características individuales como colectivas, y
sus interacciones, sobre una respuesta en
individuos
Datos
j
i
1
1
2
2
3
3
4
4
5
5
Yij
1
2
1
2
1
2
1
2
1
2
5
7
4
6
3
5
2
4
1
3
Xij
1
3
2
4
3
5
4
6
5
7
Gráfico de puntos
Regresión a nivel micro (total)
Yij=5.33 - .33*Xij + eij
Regresión entre grupos
Y. j  8.0  1.0 * X. j  e
Fitted values
8
7
6
5
4
3
2
1
0
0
1
2
3
4
Xij
5
6
7
8
Regresión dentro de los grupos
Yij  Y. j  1.0(Xij  X. j )  e
Fitted values
8
7
6
5
4
3
2
1
0
0
1
2
3
4
Xij
5
6
7
8
Resumen
Fitted values
8
7
6
Dentro
5
4
3
Total
2
Entre
1
0
0
1
2
3
4
Xij
5
6
7
8
Modelo Multinivel (MMn)
• Respuesta puede expresarse como una
función de la relación entre y dentro de los
grupos
Yij  Y. j  1.0 * ( X ij  X ij )  e
 (8.0  1.0 * X ij )  1.0 * ( X ij  X ij )  e
 8.0  2.0 * X . j  1.0 * X ij  e
Caso: Individuos anidados en conglomerados
• Opcion 1: Ignorar pertenencia a los grupos
• Enfasis: Variabilidad entre los individuos
y/o en los atributos a nivel de individuos
• Problema:
– Violación del supuesto de independencia entre
las observaciones
– EE incorrectos
– Estimadores ineficientes
Caso: Individuos anidados en conglomerados (2)
• Opcion 2: Usar datos a nivel de grupo
• Enfasis: Variabilidad entre grupos
• Problema:
– Ignora la estructura jerárquica de los datos
– Pérdida de informacion
– Ignora el papel del nivel individual en el estudio de la
variable de respuesta
• Opciones 1 y 2 usan solo variables de un nivel
ignorando la estructura de los datos
Caso: Individuos anidados en conglomerados (3)
• Opcion 3: Definir distintos modelos para
cada grupo
• Enfasis: Coeficientes difieren de grupo en
grupo
• Problema:
– No examina el efecto grupal en la respuesta de
nivel individual
– No es factible cuando hay un gran número de
grupos o una pequeña cantidad de
observaciones en los grupos
Caso: Individuos anidados en conglomerados (4)
• Opcion 4: Incluir variables indicadoras de grupo
en el nivel individual
• Enfasis: Ajustar diferentes modelos a cada grupo
• Problema:
– No permite examinar el efecto de la variable grupal en
la respuesta
– Asume que los grupos no estan relacionados
– Ignora el hecho de que los grupos pueden provenir de
una poblacion mas grande de grupos
MMn
• Permite la evaluación simultánea de los efectos a
nivel individual y grupal
• Considera la no independencia de las
observaciones al interior de los grupos
• Los grupos no se tratan como no relacionados,
pero son vistos como provenientes de una gran
población de grupos
• Se puede examinar simultáneamente la
variabilidad entre individuos y entre grupos
Ejemplo 2 niveles
• Estructura anidada de dos niveles
Ejemplo 3 niveles
Preguntas de Investigación
1. Hay diferencia en el progreso de los estudiantes hombres comparado con el
de las mujeres?
2. Hay variación entre las escuelas en la brecha de progreso entre hombres y
mujeres?
3. La variabilidad del progreso es distinta entre hombres y mujeres?
4. Cual es la variabilidad en el progreso entre las escuelas?
5. El efecto en la escuela X es distinto que el de las otras escuelas en la
muestra?
6. Hay mayor variabilidad en el progreso entre las escuelas en estudiantes con
bajo puntaje inicial?
7. Hay mas progreso en estudiantes de escuelas privadas comparado con las
publicas?
8. El progreso de los estudiantes de escuelas publicas es menos variable?
9. Las mujeres presentan mayor progreso en las escuelas estatales?
Ejemplo 3 niveles: Diseño de corte transversal en el
tiempo (estudiantes dentro de cohortes dentro de
escuelas)
4 niveles
Que se modela?
1. Hay diferencia en el progreso de los estudiantes hombres comparado con el
de las mujeres?
2. Hay variación entre las escuelas en la brecha de progreso entre hombres y
mujeres?
3. La variabilidad del progreso es distinta entre hombres y mujeres?
4. Cual es la variabilidad en el progreso entre las escuelas?
5. El efecto en la escuela X es distinto que el de las otras escuelas en la
muestra?
6. Hay mayor variabilidad en el progreso entre las escuelas en estudiantes con
bajo puntaje inicial?
7. Hay mas progreso en estudiantes de escuelas privadas comparado con las
publicas?
8. El progreso de los estudiantes de escuelas publicas es menos variable?
9. Las mujeres presentan mayor progreso en las escuelas estatales?
Otros ejemplos de 2 niveles
•
•
•
•
Medidas repetidas en el tiempo
Datos de panel
Encuestas multietapicas
Estudios de intervención donde la
intervención es a nivel grupal.
Medidas repetidas en el tiempo
Estudio experimental por grupo
Estrategia de Modelamiento
• Modelo a 1 nivel para la media
Yi   0  ei
i  1,2,3,....., n
 0  Y
ei  Yi   0
residuo
ei  N (0,  )
2
MMN para 2+ promedios
Yij   0   j  eij
i  1,2,...n j
j  1,2,...J
nivel
nivel
sujeto
grupo
donde
 0 : media global
eij  Yij  (  0   j ) residuo individual
Si Y j es la media grupo j  Y j   0   j
  j  Yj  0
residuo nivel grupo
eij  N (0,  e2 )
 j  N (0,  2 )
Modelo de componentes de
varianza: Varianza dentro y
varianza entre grupos
Coeficiente de partición de
varianza
 2
CPV  2
    e2
• CPV equivale al coeficiente de correlación
intraclase en el caso de un MMN simple.
• Si el CPV es 0.2, podríamos decir que el 20% de la
variación es entre grupos y que el 80% es dentro
de los grupos.
• La correlación entre pares de individuos
seleccionados al azar de un mismo grupo es de 0.2.
Prueba para efecto de grupo
• La hipótesis de nulidad es H0: σ2µ=0
• LRT (prueba de razón de verosimilitud) LRT=2{log(L1) – log(L2)} ~ χ2(p)
MMn para 2 niveles
• Modelo:
– Sistema de ecuaciones bi-etápico
– La variabilidad dentro del grupo es explicada
por una ecuación a nivel individual
– La variabilidad entre grupos en los coeficientes
especificos de grupo es explicada por una
ecuación a nivel de grupo
Planteamiento del Modelo
• J grupos con Nj individuos en cada grupo
• Yij variable de respuesta en el individuo i del grupo j (j=
1,…, J; i= 1, Nj)
• Xij variable explicatoria a nivel individuo
• Zj variable explicatoria a nivel de grupo
• Para cada grupo tenemos una regresión
Yij  0 j  1 j * Xij  ij
• Los  son modelados por la var expl del grupo
0 j   00   01 * Z j   0 j
1 j  10  11 * Z j  1 j
Ilustración
1 predictor a nivel individual y 1 predictor a nivel grupal
1era Etapa
Yij  oj  1 j * Xij  ij ij ~ N0, 2 
Respuesta individuo i
en grupo j
Var explicatoria nivel
individual en individuo i
en grupo j
Independientes
dentro de cada grupo
2da Etapa: Coef de regresión especifico para cada grupo es modelado
Como una función de la variable de nivel grupal
0 j   00   01 * Z j   0 j
1 j  10  11 * Z j  1 j
Cov 0 j , 1 j   10
 0 j ~ N0, 00 
1 j ~ N0, 11 
Var explicatoria nivel grupal
Interpretación
• 0j mide la desviación del intercepto del grupo en
relación al intercepto global 00 ajustado por el
efecto de la variable grupal
• 1j mide la desviación de la pendiente del grupo
en relación a la pendiente global 11 ajustado por
el efecto de la variable grupal
• 01 representa la covarianza entre interceptos y
pendientes
Resumen
• MMn resume la distribución de los coeficientes
específicos de grupo en:
– Una parte fija que es constante a traves de los grupos
([00 ,01] para interceptos y [10 ,11] para pendientes)
– Una parte aleatoria (0j para intercepto y ij para
pendiente) que puede variar de grupo en grupo
– Supuesto: macro-errores 0j y ij son independientes
del nivel de error individual ij
Taller
Análisis de Datos Multinivel
Sergio R. Muñoz, Ph.D.
CIGES & Departamento Salud Publica
Facultad de Medicina
Universidad de La Frontera
munozs@ufro.cl
12-25 de Mayo, 2012