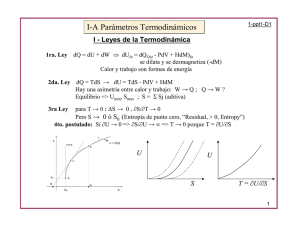
Relaciones Fundamentales
Anuncio

CAPITULO 4. RELACIONES ENTRE LAS LEYES TERMODINAMICAS . Energía libre de Gibbs y Helmholtz. Potencial químico, fugacidad, coeficiente de fugacidad, actividad, coeficiente de actividad. Aplicaciones en sustancias reales Prof. Silvia Calderón Sección 02 Objetivos Combinar la primera y segunda ley de la Termodinámica para desarrollar la definición de las funciones de Energía Libre de Helmholtz (A) y Energía Libre de Gibbs (G) Conocer la aplicabilidad de las funciones termodinámicas A y G como criterios de equilibrio y espontaneidad Objetivos Combinar la primera y segunda ley de la Termodinámica para desarrollar las cuatro relaciones fundamentales Analizar las cuatro relaciones fundamentales para desarrollar las expresiones de las Relaciones de Maxwell Objetivos Conocer la aplicabilidad de las Relaciones de Maxwell en la determinación de las propiedades residuales Sistema Para simplificar el desarrollo de las ecuaciones que siguen, estudiaremos un sistema: Cerrado Homogéneo De composición constante Sin reacción química Trabajo (W) Sistema Calor (Q) Primera Ley de la Termodinámica d mU mentra H Ek E p m sale H Ek E p Q W entra sale dt mU final t final d mU Q W dt tinicial mU inicial mU QT W T Recordemos que W puede indicar: •Trabajo halar-empujar •Trabajo de compresión-expansión •Trabajo eléctrico •Trabajo para crear superficies m ctte U Q W (Todos por ud. de masa) En forma diferencial: dU Q W A) Segunda Ley de la Termodinámica d mS Q mentra S entra m sale S sale S generada dt Talrededores Q d mS S generada dt Talrededores tinicial mS inicial QT mS S T generada Talrededores mS final t final m ctte S Q Talrededores S generada (Todos por ud. de masa) En forma diferencial: dS Q T dS generada B) Segunda Ley de la Termodinámica dS Q T dS generada dS generada 0 dS generada 0 Procesos Reversibles B) C) dS generada 0 Procesos Irreversibles Combinacion entre las leyes De B) tenemos que: Introducimos en A) Q TdS TdS generada dU Q W dU TdS TdS generada W dU TdS generada TdS W Como : dS generada 0 dU TdS W Combinacion entre las leyes dU TdS W dU TdS W Proceso Reversible D) dU TdS W Proceso Irreversible “Un proceso evolucionando espontáneamente (irreversiblemente) hacia un estado de equilibrio, tiende a un mínimo de energía” (Belandria, 1996) “El Universo tiende a un máximo de entropía” Suposiciones Adicionales “Si el único condicionante es la presión externa sobre el sistema, entonces el único trabajo es el Trabajo Mecánico contra la presión exterior” (Klotz, 1977) W PdV dU TdS PdV E) F) Criterio de Equilibrio y Espontaneidad dU TdS PdV F) Para que un proceso pueda efectuarse espontáneamente (sin la adición/sustracción de energía desde/hacia los alrededores) es necesario que se cumpla la desigualdad. El sistema se moverá entonces hacia la posición de equilibrio más próxima, en busca de alcanzar un mínimo en su energía total, mientras que la entropía del universo (sistema+alrededores) alcanza un máximo. Energía Libre de Helmholtz Si suponemos que nuestro sistema está sometido a un proceso donde la temperatura (T) y el volumen permanecen constantes, la expresión F) se puede escribir como: dU TdS SdT PdV SdT 0 T ctte PdV 0 V ctte d U TS 0 Energía Libre de Helmholtz De acuerdo a lo anterior, se tiene que la cantidad U-TS disminuye cuando el sistema se moviliza espontáneamente hacia el equilibrio. d U TS 0 De aqui que: A U TS Por tanto: dA 0 A representa la llamada energia libre de Helmholtz, y su valor: •Disminuye (dA <0) si el sistema se desplaza espontáneamente al equilibrio (procesos irreversibles) •Permanece constante, con dA=0 si el sistema se desvía infinitesimalmente del equilibrio (procesos reversibles), es decir está en equilibrio (dinámico). •Aumenta (dA >0) si el sistema no puede desplazarse espontáneamente al equilibrio, sino que amerita de energía Energía Libre de Gibbs Si suponemos que nuestro sistema está sometido a un proceso donde la temperatura (T) y la presión (P) permanecen constantes, la expresión F) se puede escribir como: dU TdS PdV dU PdV VdP TdS SdT 0 SdT 0 T ctte VdP 0 P ctte Si H U PV dH dU PdV VdP dH TdS SdT 0 d H TS 0 Energía Libre de Gibbs De la misma forma, como U tiende a un mínimo, H debe tender a un mínimo; y como S tiende a un máximo, se tiene que la cantidad H-TS disminuye cuando el sistema se moviliza espontáneamente hacia el equilibrio. d H TS 0 De aqui que: G H TS Por tanto: dG 0 G representa la llamada energía libre de Gibbs, y su valor: •Disminuye (dG <0) si el sistema se desplaza espontáneamente al equilibrio (procesos irreversibles) •Permanece constante, con dG=0 si el sistema se desvía infinitesimalmente del equilibrio (procesos reversibles), es decir esta en equilibrio (dinámico). •Aumenta (dG >0) si el sistema no puede desplazarse espontáneamente al equilibrio, sino que amerita de energía Energía Libre? G H TS A U TS A y G se denominan energía libre porque son un indicativo de la energía máxima que posee un sistema aprovechable para realizar trabajo útil. Ambas son funciones de ESTADO por estar definidas en términos de otras funciones de estado Recordemos que si el sistema es capaz de transferir parte de su energía como calor, nunca se podrá aprovechar el 100 % de ésta para realizar trabajo. Así vemos que al transferir este calor (δQ=TdS), el sistema obliga a que se genere un cambio de entropía en el universo. La energía del sistema que no se puede aprovechar para realizar trabajo es, por tanto, proporcional a la relación TS Primera Relación Fundamental Entre la 1era y 2da Ley de la Termodinámica Recordemos que combinando las ecuaciones de la primera y segunda ley se obtuvo: dU TdS PdV F) Para procesos reversibles donde dSgenerada=0 se transforma en: dU TdS PdV G) Segunda Relación Fundamental Entre la 1era y 2da Ley de la Termodinámica Recordemos a la entalpia: H U PV dH dU VdP PdV Sustituyendo en G) dH PdV VdP TdS PdV dH TdS VdP H) Problema: Las dos primeras relaciones tienen a S como variable independiente y esta no puede medirse directamente Tercera Relación Fundamental Entre la 1era y 2da Ley de la Termodinámica Buscamos solucionar el problema haciendo uso de A y G A U TS dA dU TdS SdT Sustituyendo en G) dA TdS SdT TdS PdV dA SdT PdV I) Utilidad: A tiene como variables independientes a T y V. Ambas pueden medirse, y por tanto podemos usarlas para estimar A Cuarta Relación Fundamental Entre la 1era y 2da Ley de la Termodinámica Buscamos solucionar el problema haciendo uso de A y G G H TS dG dH TdS SdT Sustituyendo en H) dG TdS SdT TdS VdP dG SdT VdP J) Utilidad: G tiene como variables independientes a T y P. Ambas pueden medirse, y por tanto podemos usarlas para estimar G Relaciones Fundamentales Entre la 1era y 2da Ley de la Termodinámica dU TdS PdV dH TdS VdP dA SdT PdV dG SdT VdP G) H) I) J) Válidas para sistemas sometidos a procesos reversibles donde el único trabajo sea pdV Relaciones de Maxwell Para que la primera relación fundamental tenga coherencia interna, es necesario que equivalga a la ecuación diferencial exacta que describe a la energía interna (U) como una función de S y V U U dU TdS PdV dU dS dV S V V S U U T P S V V S Donde : U U V S S V T P V S S V Primera Relación de Maxwell Relaciones de Maxwell Para que la segunda relación fundamental tenga coherencia interna, es necesario que equivalga a la ecuación diferencial exacta que describe a la energía interna (H) como una función de S y P H H dH dS dP S P P S dH TdS VdP H T S P H V P S Donde : H P S H S P T V P S S P Segunda Relación de Maxwell Relaciones de Maxwell De la misma forma para que la tercera y cuarta relaciones fundamentales tengan coherencia interna, es necesario que equivalgan a la ecuación diferencial exacta correspondiente dA SdT PdV A S T V dG SdT VdP A G P S V T T P G V P T S P V T T V S V P T T P Tercera Relación de Maxwell Cuarta Relación de Maxwell Relaciones de Maxwell La tercera y cuarta relaciones de Maxwell fueron de gran utilidad para hallar las expresiones que nos permiten calcular U, H y S para cualquier sustancia a partir de las propiedades residuales V UR T P( T, V ) P( T, V ) dV T V R S ( T , V ) P ( T , V ) d V R ln ( z ) R V T P HR 0 VT V( T, P ) dP T P S ( T , P ) R 0 R V ( T , P ) d P T P Referencias Belandria, José Iraides (1996) Termodinámica: Historia, Leyes y Reflexiones. Consejo de Publicaciones de la Universidad de Los Andes. Mérida, Venezuela KLOTZ, I.M. y ROSENBERG, R. M (1977).Termodinámica Química. Editorial ac, Madrid, España