Parámetros Termodinámicos
Anuncio

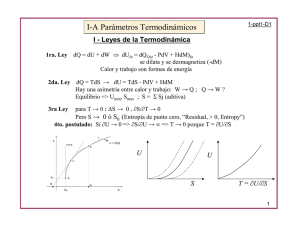
1-ppt1-D1 Parámetros Termodinámicos I - Leyes de la Termodinámica 1ra. Ley Calor y trabajo son formas de energía dQ = dU + dW ⇒ dU = dQin - PdV +HdM se dilata y se desmagnetiza (-dM ~ H / T) dQ PdV HdM dUin 2da. Ley dQ = TdS → dU = TdS - PdV + HdM Hay una asimetria entre calor y trabajo? = W → Q ; Q → W ? Equilibrio => Umin, Smax ; S = Σ Sj (aditiva) 3ra Ley para T → 0 : ∆S → 0 , ∂S/∂T → 0 Pero S → 0 ó S0 (Entropía de punto cero, “Residual, > 0, Entropy”) 4to. postulado: Puesto que T se define como T = ∂U/∂S para que T → 0 es necesario que ∂U → 0 La condición de T = 0 es para ∂U = 0, no para ∂S ! 12 Entropía como máquina criogénica Temperatura, de quién?. H0 isotérmico H1 adiabácitico 1963 en BT → 20mK ; hoy con Cu y Pt → µK 13 Tipo de parámetros intensivos (T, p, h..E,Tension..., µ) (Σ Tj = ?) extensivos (S, V, M...D, Deform.., N) (Σ Vj = Vtot) si Y conjudado de X → Y = δG/ δX pseudo intensivos: por unidad de masa, de volumen, ..... Externos (controlables) e Internos (no controlables): parámetros de control (externos) = Presión, Campo, Composición ej: CV ≠ CP (CH vs CM) parámetros internos = orden configuracional, defectos Abriata & Laughlin; Prog. Mater. Sci 49 (2004) 367 14 (bolzmanones) +1/2 n - 1/2 E T1 Boltzman < T2 H T2 Mec. Cuántica vs Estadística BL(ε) = e(-E/kT) Parámetros ‘emparentados’ H T1i Tiempos característicos τ(∆=2H) << τ(spin-fonón) [adiabatico] -H “H/T” T1f T1f > 0 ó < 0 ? 15 Tipo de partículas Partículas vs Quasipatículas Tipos de distribuciones: Bose-Einstein BE(ε) = 1/(e(E-Ef)/kT - 1) Ppio. exclusión: Bosones Fermi-Dirac F(ε) = 1/(e(E-Ef)/kT + 1) Fermiones Maxwell. - Boltzmann BL(ε) = e(-E/kT) Partic. Clásicas Sistemas independientes Vs. Correlacionados single particles: Σ(c/u) estados colectivos; MO - CDW – SDW Paramagnetismo (T > Tord) Orden Magnético (Tord > T) 16 Función de estado: si una función u(x,y) tiene un valor inicial defnido, p.ej. ui= 0 y su valor solo depende del estado final uf(x,y), entonces “u” es una función de estado. Hay 4 (usuales) funciones de estado: Energia Interna: U(S, V, -M) → dU =TdS - pdV + hdM [U = Q – W] Entalpia: E(S, p, h) → dE=TdS + Vdp – Mdh [E = U + W] Potencial de Helmholtz: F(T, V, -M) → dF= - SdT - pdV + hdM [F = U –TS] Potencial de Gibbs: G(T, p, h) → dG= - SdT + Vdp - Mdh (intensivos) [G = F + W] dG = - SdT + Vdp - Mdh – µdN δG/ δxi: δ2G/ δxi2: δ2G/ δxiδyj : S V -M CP / T κ χ αth µ(εF) ? λH (αth = Expans.Térmica, λH = Magnetostricción) medibles: Cp ; V ; M → S ; γT ; αth ; λH ; χ 17 Relaciones entre parámetros “magnéticas” “mecánicas” Relaciones de Maxwell La Materia Condensada no es un gas de partículas ! (o si ?) 18 Relaciones entre parámetros Volumen vs Presión (CP – CV ) / T =(∂S /∂T)P - (∂S /∂T)V = (∂S/∂P)T (∂P/∂T)V Maxwell => (∂S/∂P)T = - (∂V/∂T)P = - V β (∂P/∂T)V = - (∂P/∂V)T (∂V/∂T)P = - (∂V/∂T)P / (∂V/∂P)T = - β / κ = V β2 / κ => CP - CV = T V β²/ κ β Sólidos => presión del “gas de electrones’ (elástica) caso CeAl3 => dependencia de las “escalas de temperatura” κ 19 Expansión Térmica ∂S/ ∂P = - ∂V/ ∂T = - α Relaciones entre parámetros Compresibilidad CP /T = f(p) → ∆S(T,P) → κ(T) T [K] 0 1 2 3 4 5 0.5 0.4 ∆Sm / Rln 2 (a) 0 GPa 0.25 0.61 1.0 1.4 κ=1/V ∂V/ ∂P ; ∂S/ ∂P α / γT = ∂S/∂P * 1/V ∂V/∂T * ∂T/ ∂S = 1/V * ∂V/∂P ss pre 0.3 0.2 div1 0.1 4 κ = dS/dp * α / γT [~ 10 /Kbar] CeCu2 (Si0.9Ge0.1 )2 -6 0.0 0.15 medido -6 -1 α [10 K ] 0.10 0.05 calculado δ S / δ p [a.u.] 0.00 1 2 3 4 2 1 0 0 -0.05 0 3 5 1 2 3 4 5 T [K] T [K] 20 Relaciones entre parámetros PRB 81 (2011) 184429 10 0T 0.3 0.5 0.7 Cm [J / mol K ] 8 2 Campo Magnético ∂S/ ∂H = ∂M/ ∂T Ce1.9Pd2.4In0.7 B = 2T 6 B = 1T 4 2 0 0 1 4 5 6 1.0 B= 1T 0.8 δM / δΤ < 0 0.6 0.4 0.2 2 4 6 T [K] 8 10 (a T > Tn) H=0 0.5 T 1T 2T 0.8 S / 2RLn2 M / B [emu / mol Oe] 3 T [K] 1.0 0.0 2 0.6 0.4 H 0.2 Ce1.9 Pd2.4 In0.7 0.0 0 1 2 3 T [K] 4 5 6 21 Parámetro de Grüneisen Sistema simple vibraciones atómicas x 10-5 Γ~2 Generalización ≠ f(T) Temperat. (energía) característica. y Volumen Demo II de Debye U = 9R T4/θ3 ∫0Xmx x3/(ex-1) dx con x = θ /T U = - T2 δ(F/T)/δT |V DemoIII 22