0 ) ( min ) ( ≠ = b divisor ador deno dividendo numerador b a 3 Re 3

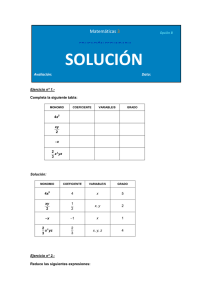
DIVISIÓN MONOMIO ENTRE MONOMIO ENTRE MONOMIO
DIVISIÓN POLINOMIO ENTRE MONOMIO
Fundamentos de Matemáticas I
División algebraica
Video Previo a la actividad: División monomio ente monomio
Video Previo a la actividad: División polinomio ente monomio
Formas de la división:
2)
a numerador(dividendo)

b0
b deno min ador (divisor)
División de monomio entre monomio.
Es importante el entendimiento de las leyes de exponentes.
Ejemplo:
1)
6x 3 y 4
 3x 32 y 47  3xy 3
2 7
2x y
2)
12a 3bm 7
1 35 14 72 1 2 3 5
m5
 a b m  a b m  Re sultado  2 3
4
48a 5 b 4 m 2 4
4a b
Re sultado 
3x
y3
División de polinomio entre monomio.
Ejemplo:
12 x 4 y 2  8 x 2 y 2  9 x3 y 4 z  4 x3 y 2

4 x3 y 2
Separa cada término del numerador entre el denominador y simplifica
aplicando leyes de los exponentes:
12 x 4 y 2 8 x 2 y 2 9 x 3 y 4 z 4 x 3 y 2
9
 3 2 
 3 2  3x 43 y 2 2  2 x 23 y 2 2  x 33 y 4 2 z  411 x 33 y 2 2
3 2
3 2
4
4x y
4x y
4x y
4x y
Re sultado :  3x 
2 9y2z

1
x
4
Ejercicios para reforzar el tema
Nombre_________________________________Matrícula____
Resuelve las siguientes divisiones de expresiones algebraicas:
I. Monomio entre monomio
1)
24a 3 bm 5

3ab 4 m 4
II. Polinomio entre monomio
1)
12a 3b3  6a 4b 2  36ab

12a 3b3
13a 4b 4  26a 3b3  52ab

2)
26a 3b3
9 x 4 y 2  3x 3 y 2  15 x y 4  5 x 5 yz

3)
3x 3 y 2
3x 4 y  9 xy  36 x  12 x3 y

4)
12 x3 y
2)
32m 5 n 6 z 8

40m 7 n 6 z 5