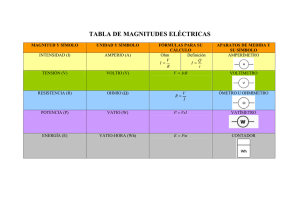
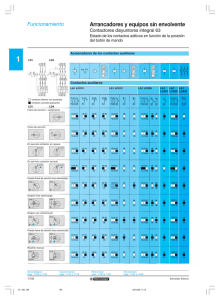
I U ··IU U I º90 ±= I U I1 I2 I3 I1 I1

Al circuito de la figura se le aplica un sistema trifásico de tensiones simétrico, equilibrado
y de secuencia directa, siendo la tensión compuesta U12=400∠30ºV. Se sabe que la lectura
del vatímetro 1 es nula (LW1=0 div) y que las lecturas de los amperímetros A1 y A3 son
iguales. En estas condiciones se pide:
1
2
3
4
Valores de las corrientes I1 , I2 , I3, y I1’ , I2’, I3’ .
Lecturas de los amperímetros: LA1, LA2, y LA3.
Valor de la impedancia Z∆ .
Lectura del vatímetro W3.
0 div.
I1
* W1
L1
I1’
*
A1
U12=400∠30ºV
I2
L2
Z∆
I2’
A2
Equilibrada
I23
*
I3
A3
L3
I3’
* W3
j20Ω
RESOLUCIÓN:
 ∧ 
LW1 = U23·I1· cosU23 I 1  = 0div


Como los valores de U23 e I1 son distintos de cero ( U 23 ≠ 0 e I 1 ≠ 0 ), en la expresión de
•
la lectura del vatímetro el factor que debe ser nulo es el coseno y por tanto el ángulo que
∧
deben formar la tensión U23 y la corriente I1 debe ser de 90º, así: U23 I1 = ± 90º .
La corriente I1 por tanto podrá situarse en dos posiciones: 90º adelantada ó 90º atrasada
respecto a la tensión U23 , véanse las posibles posiciones de la corriente en el diagrama
vectorial:
U30=230∠120ºV
U12=400∠30ºV
U31=400∠150ºV
U10=230∠0ºV
I1
I1
U20=230∠-120ºV
De las dos posibles soluciones de I1 , la solución I1= I1 ∠180º no es posible ya que desfasa más
de ±90º de la tensión simple de su fase U10. Por tanto la solución es I1= I1 ∠0º= I1’.
U23=400∠-90ºV
Luego: I1’= I’ ∠0º, I2’= I’ ∠-120º, I3’= I’ ∠120º. Por ser la carga equilibrada.
Además sabremos que Z∆ es resistiva por no haber desfase entre U10 e I1.
•
LA1 = LA3
Eso significa que : I 1 = I 3 ; I1= I1’.
Se da asimismo la circunstancia de que I 3 = I '3 −I 23 , y que I23 es conocida
I 23 =
400∠ − 90 º
20∠90 º
= 20∠180 º A
Las corrientes serán las siguientes:
Como la carga Z∆ es equilibrada, se cumple: I '1 = I '2 = I '3 .
Para que se cumpla que I 1 = I 3 = I '1 , es decir que las lecturas de los amperímetros 1 y
3 sean iguales ( LA1 = LA3 ), el triángulo formado por las corrientes , I3’, -I23 e I3 deberá
ser equilátero. Ya que I3’, e -I23 forman un ángulo de 60º, luego I3’=20∠120º A.(*)
Por todo ello:
I 1' = I 2' = I 3' = − I 23 = 20 A
U30=230∠120ºV
U31=400∠150ºV
U12=400∠30ºV
30º
-I23
I3’
60º
30º
I23
U10=230∠0ºV
I1’=I1
I2
I23
I2’
U20=230∠-120ºV
U23=400∠-90ºV
1 Las corrientes serán las siguientes:
I 1' = 20∠0 º A
I 2' = 20∠ −120 º A
I 3' = 20∠120 º A
I 1 = I 1' = 20∠0 º A
I 2 = I 2'+I 23 = 20∠ −120 º + 20∠180º = 20 3 ∠ -150º A
I 3 = I 3'−I 23 = 20∠120 º + 20∠0º = 20∠60º A
2 Las lecturas de los amperímetros:
LA1 = LA3 = 20A
LA2 = 20 3A
3 Valor de la impedancia Z∆:
Z
estrella
Z
∆
 400 


U 10  3  ∠0 º  20 
=
=
=
Ω

I 1'
20∠0 º
 3  ∠0 º
 20 
= 3·
= 20 3 ∠0º Ω

 3  ∠0º
4 Lectura del vatímetro W3 :
[
]
[
]
[
]
LW3 = ℜe [U 12· I 3 *] = ℜe 400∠30 º ·20∠60 º * = ℜe 8000∠ −30 º = ℜe 4000 3 − j 4000 = 4000 3div
o:
∧


LW3 = U12·I 3· cosU 12 I 3  = 400·20·cos 30 º = 4000 3div


(*) Quien no desee hacerlo gráficamente apoyándose en el diagrama vectorial, habría
llegado a la misma solución de la siguiente forma:
I 3 = I 3'−I 23 entonces, I 3 = I 3'−I 23 e I 3 = I 1 = I 1'
Además I 23 =
400∠ − 90 º
20∠90 º
= 20∠180 º A ;
−I 23 = 20∠0 º A
luego:
I 3 = I 3'+20∠0 º
I '= I '∠120 º +20∠0 º
1
3
I '= − I '+ j
I '+20 operando
2
2
2
2
2 
1 
3 

I '= 20 − I ' + 
I '
2 

 2

2
o
 3 
I '2 3 2
1 

I '2 = 20 − I ' + 
I ' → I '2 = 400 − 20I '+
+ I ' → 20I ' = 400 → I ' = 20A
2 
4
4

 2
