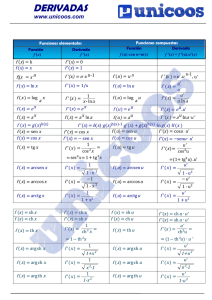
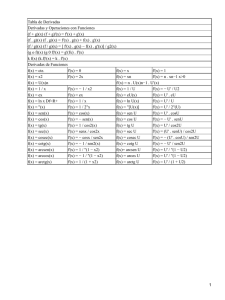
Tabla de derivadas y equivalentes
Anuncio
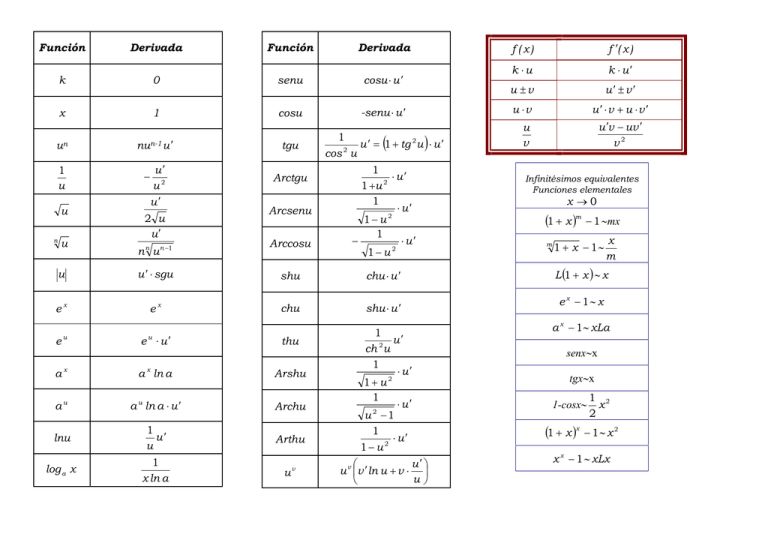
Función Derivada Función Derivada k 0 senu cosu ⋅ u ′ x 1 cosu -senu ⋅ u ′ tgu 1 u ′ = 1 + tg 2 u ⋅ u ′ 2 cos u un 1 u u n u nun-1 u ′ − u′ u2 u′ 2 u u′ n n u n −1 ( 1 ⋅ u′ 1 +u 2 1 ⋅ u′ 2 1− u 1 − ⋅ u′ 2 1− u Arctgu Arcsenu Arccosu u u ′ ⋅ sgu shu chu ⋅ u ′ ex ex chu shu ⋅ u ′ eu e u ⋅ u′ thu ax a x ln a Arshu au a u ln a ⋅ u ′ Archu lnu 1 u′ u Arthu log a x 1 x ln a uv ) 1 u′ ch 2 u 1 ⋅ u′ 1+ u2 1 ⋅ u′ u 2 −1 1 ⋅ u′ 1− u2 u′ u v ′ ln u + v ⋅ u v f ( x) f ′( x ) k ⋅u k ⋅ u′ u ±v u′ ± v ′ u ⋅v u′ ⋅v + u ⋅v ′ u ′v − uv ′ v2 u v Infinitésimos equivalentes Funciones elementales x →0 (1 + x )m m − 1 ∼mx 1 + x − 1∼ x m L (1 + x ) ∼ x ex − 1∼ x a x − 1∼ xLa senx∼x tgx∼x 1-cosx∼ (1 + x )x 1 2 x 2 − 1∼ x 2 x x − 1 ∼ xLx