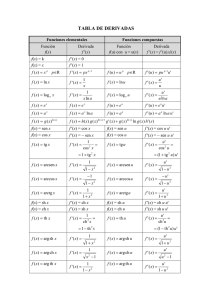
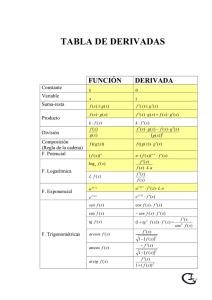
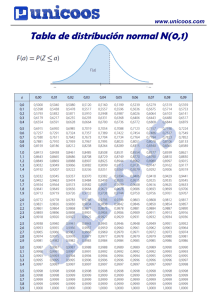
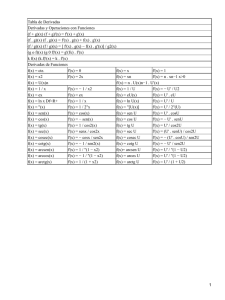
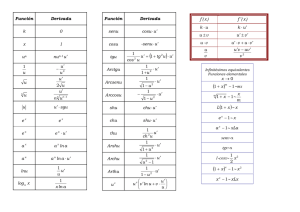
Tabla de Derivadas 19 770.43 KB

DERIVADAS
www.unicoos.com
Funciones elementales
Función
Derivada
f (x)
f '(x)
Funciones compuestas
Función
Derivada
f (u) con u=u(x)
f '(x) = f '(u).u'(x)
f (x ) = k
f (x ) = x
f '(x) = 0
f '(x) = 1
f ( x) = ln x
f '(x ) = 1/x
f ( u) = ln u
f '(x ) = e x
f ( x) = a x ln a
f(u) = a u
f )(x = x n
f ( x ) = log
f ( x) = e x
f ( x) = a x
f '(x) = n .x n-1
a
x
f (x ) = g (x )h(x)
f (x) = sen x
f (x) = cos x
f ( x) = tg x
f ( x) = arcsen x
f ( x) = arccos x
f ( x) = arctg x
f (x ) = sh x
f (x ) = ch x
f '(x ) =
1
x . ln a
n-1
f ( u ) = log u
a
f (u ) = e u
f '(x ) =n .u
u'
f '( x) =
u
u'
f '( x) =
u .ln a
f '(x) = e u .u'
f ( u) = arcsen u
f '( x ) =
. u'
f '(x ) = a u .lna . u '
f '(x) = h(x) .g (x)h(x)-1 .g '(x) + g (x)h(x) .ln g (x) .h'(x )
f (u) = sen u
f '(x ) = cosu . u '
f '(x) = cos x
f (u) = cos u
f '(x) = − sen x
f '(x ) = −senu . u '
1
u'
=
f ( u) = tg u
f '(x ) =
f '(x )=
cos² x
cos²u
= sec²x = 1 + tg²x
=(1+ tg²u) .u'
1
f '( x ) =
f '( x ) =
f '( x ) =
1 -x ²
−1
1-x²
1
1 + x²
f (x ) = th x
f '(x) = ch x
f '(x) = sh x
1
f '(x ) =
=
ch ² x
f ( x) = arg sh x
f '( x ) =
f ( x) = arg th x
x²-1
1
f '( x ) =
1-x²
f ( x) = arg ch x
f (u ) = u n
= 1 − th ²x
f '( x ) =
1
1+x²
1
f ( u) = arccos u
f ( u) = arctg u
f (x ) = sh u
f (x ) = ch u
f ( x) = th u
f ( x) = arg sh u
f ( x) = arg ch u
f ( x) = arg th u
f '( x ) =
f '( x ) =
u'
1 - u²
−u'
1 - u²
u'
1 + u²
f '(x ) = ch u . u '
f '(x ) = sh u . u '
u'
f '(x ) =
=
ch²u
= (1− th ²u ) . u '
f '( x ) =
f '( x ) =
u'
1+u²
u'
u²-1
u'
f '( x ) =
1-u²