mecanismos de leva y seguidor - Universidad Tecnológica de Pereira

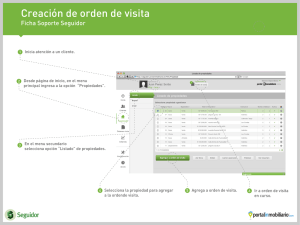
LECCIÓN 11
MECANISMOS DE LEVA Y SEGUIDOR
Al proyectar una máquina es necesario elegir el mecanismo o serie de mecanismos que deben entrar en su
composición partiendo de las operaciones a realizar el trabajo de la misma. Por tanto, los mecanismos se
seleccionarán de forma que el movimiento del eslabón conducido se atenga a una determinada ley.
En algunas máquinas se requiere que el eslabón conducido siga una ley de movimiento complejo. Una solución
sencilla, compacta y económica es el mecanismo leva-seguidor; adicionalmente, este tipo de mecanismo tiene la
ventaja que son fáciles de diseñar movimientos del seguidor que tengan casi cualquier característica deseada.
Una leva es un elemento mecánico que sirve para impulsar, por contacto puntual o lineal, a otro elemento, llamado
seguidor, para que éste desarrolle un movimiento específico.
Un mecanismo leva-seguidor consiste de dos eslabones móviles, con coordenada generalizada ϕ para la leva y s para
el seguidor, que se ponen en contacto mediante un par superior, ambos eslabones están unidos al bastidor mediante
un par inferior –Fig. 11.1. De esta manera se obtiene un mecanismo de un grado de libertad en el que se define una
ley de dependencia –s(ϕ)– entre la coordenadas que describen el movimiento de la leva y del seguidor; esta ley
recibe el nombre de ley de desplazamiento del seguidor.
bastidor
seguidor
s(ϕ)
leva
ϕ
bastidor
e
Figura 11.1 Mecanismo leva seguidor
En el mecanismo de leva-seguidor, dada la ley de movimiento giratorio de la leva, el seguidor se desplazará también
según una ley de movimiento completamente determinada, que depende del contorno (perfil) de la leva y el tipo de
seguidor. Por consiguiente, dándole a la leva y al seguidor una determinada forma se puede obtener la ley de
movimiento requerida para el seguidor.
11.1 CLASIFICACIÓN DE LOS MECANISMOS LEVA SEGUIDOR
Entre las características más importantes de los mecanismos levas-seguidor, se destaca su versatibilidad y
flexibilidad para el diseño. Esto conduce a una gran variedad de perfiles y formas, y a la necesidad de utilizar una
terminología para diferenciarlas.
La clasificación de los mecanismos leva-seguidor puede realizarse utilizando diferentes criterios: la geometría de la
leva, la geometría del seguidor, el tipo de cierre del par superior, la ley de desplazamiento, entre otros.
LECCIÓN No 11. MECANISMO LEVA SEGUIDOR
11.1.1 Según la geometría de la leva
Las levas se clasifican según sus formas básicas. En la Fig. 11.2 se presentan cuatro tipos diferentes de levas: leva de
disco, leva de cuña, leva de tambor y leva de cara. La menos común es la leva de cuña ya que requiere de un
movimiento alternativo de entrada en lugar de un movimiento continuo y la leva más común es la leva de placa.
4
4
2
3
2
s(ϕ)
s(x)
3
ϕ
x
1
1
a) Leva de disco o de placa
b) Leva de cuña
4
4
s(ϕ)
3
3
ϕ
1
2
ϕ
2
θ(ϕ)
1
c) Leva de tambor
d) Leva de cara
Figura 11.2 Geometría básicas de la leva
b) De acuerdo con la geometría del seguidor
Los sistemas de leva seguidor se clasifican por la geometría del seguidor. El seguidor de la Fig. 11.1 es un seguidor
de cara plana o seguidor plano, los seguidores de la Fig. 11.2 son conocidos como seguidor de rodillo, éste es el más
común. En la Fig. 11.3.a se presenta el seguidor puntual y en la Fig. 11.3.b el seguidor curva o forma de hongo.
3
3
2
2
s(ϕ)
s(ϕ)
ϕ
ϕ
1
1
e
a) Puntual
b) Curvo o forma de hongo
Figura 11.3 Formas del seguidor
11.2
FACULTAD DE INGENIERÍA MECÁNICA – UNIVERSIDAD TECNOLÓGICA DE PEREIRA
c) De acuerdo con el tipo de cierre del par superior
El enlace leva-seguidor es, en principio, unilateral ya que se produce por contacto directo, puntual o lineal, entre
ambos elementos formando un par cinemático superior. El contacto permanente leva-seguidor se puede conseguir de
dos formas, éstas son:
1) Con cierre por fuerza: se requiere de la aplicación de una fuerza externa que actúe sobre el seguidor (el propio
peso del seguidor o la fuerza de un resorte) con el objeto de mantener el contacto entre la leva y el seguidor,
Fig. 11.4.a.
2) Con cierre por forma: Estas levas se denominan desmodrómicas. La forma geométrica de la leva y del seguidor,
garantiza el contacto permanente entre los elementos. Existen dos casos, uno en que la leva y el seguidor tienen
dos puntos de contacto opuestos, Fig. 11.4.c, y otro en el que existe otra leva que entra en contacto con un
seguidor doble, Fig. 11.4.d.
4
2
resorte
4
3
2
3
s(ϕ)
ϕ
s(ϕ)
ϕ
1
1
a) Cierre por fuerza (peso o resorte)
b) Mecanismo de leva con rodadura
3
ϕ
2
3
4
ϕ
θ(ϕ)
s(ϕ)
1
2
1
c) anchura constante
d) Leva conjugada
Fig. 11.4 Formas de cerrar el par superior
d) De acuerdo con el movimiento del seguidor
Otro método para clasificar las levas es de acuerdo con el movimiento permitido entre el seguidor y el bastidor, estos
son:
1) Seguidor con movimiento de traslación: La dirección del movimiento del seguidor con respecto al eje de
rotación de la leva determina el tipo de movimiento, así se tienen seguidores:
•
Radiales; el eje del seguidor pasa por el eje de rotación de la leva –Fig. 11.2.a y 11.3.a.
•
Excéntricos; el eje del seguidor no pasa por el eje de rotación de la leva –Fig. 11.1 y 11.3.b.
•
Axiales; cuando el seguidor se mueve paralelo al eje de rotación de la leva – Fig. 11.2.d.
2) Seguidor de rotación: Presenta movimiento oscilatorio, el eje del seguidor puede ser paralelo – Fig. 11.4.d– o no
al eje de rotación de la leva – Fig. 11.2.c.
3) Seguidor con movimiento complejo: El seguidor hace parte de un mecanismo.
11.3
LECCIÓN No 11. MECANISMO LEVA SEGUIDOR
11.2 ANALÓGO DE VELOCIDADES Y ACELERACIONES
Para el análisis cinemático de mecanismos resulta cómodo expresar las velocidades y aceleraciones de sus puntos y
de sus eslabones en función de la coordenada generalizada del eslabón de entrada: ángulo de giro ϕ ó del
desplazamiento s del eslabón conductor. Así, sí el ángulo de giro ϕk del eslabón k está dado en forma de función
ϕk = ϕk(ϕ), entonces la velocidad angular ωk de este eslabón puede ser expresada así:
ωk =
d ϕk d ϕk d ϕ
dϕ
=
= ω k = ω ωϕk = ω ϕ 'k
dt
dϕ d t
dϕ
donde
ω es la velocidad angular del eslabón conductor, en rad/s
ωϕk = ϕ 'k =
d ϕk
es la velocidad angular adimensional del eslabón k.
dϕ
La velocidad angular adimensional ϕ 'k del eslabón k se denomina análogo de la velocidad angular del eslabón k.
De esta manera la velocidad angular ωk del eslabón k es igual al producto de la velocidad angular ω del eslabón
conductor por el análogo de velocidad angular ϕ 'k del eslabón k.
Derivando la velocidad angular con respecto al tiempo, se obtiene la magnitud de la aceleración angular αk del
eslabón k:
αk =
d ωϕk
d ωϕk d ϕ
d ωϕk
d ωk
d
dω
= ( ωωϕk ) = ω
+ ωϕk
=ω
+ ωϕk α = ω2
+ ωϕk α
dt
dt
dt
dt
dϕ d t
dϕ
= ω2
d  d ϕk

dϕ  dϕ
2

2 d ϕk
+ ωϕk α = ω2 ϕ ''k + ωϕk α = ω 2 α ϕk + α ϕ 'k
 + ωϕk α = ω
2
dϕ

donde
α ϕk = ϕ ''k es el análogo de la aceleración angular del eslabón k.
De manera análoga puede ser obtenida las ecuaciones de la velocidad y de la aceleración de cualquier punto m del
eslabón k. Sea rm el radio vector (también llamado vector posición) que determina la posición del punto m con
respecto a un sistema de coordenadas. Como se sabe de los cursos de mecánica, la velocidad vm y la aceleración am
del punto m pueden ser determinados derivando consecutivamente al radio vector rm con respecto al tiempo:
vm =
d rm d rm d ϕ
dr
=
= ω m = ω vϕm = ω r 'm
dt
dϕ d t
dϕ
donde
vϕ es el análogo de velocidad del punto m y sus unidades son de longitud
De esta manera la velocidad real vm del punto m es igual al producto de la velocidad angular ω del eslabón conductor
por el análogo de velocidad vϕ del punto m.
Derivando la velocidad del punto m con respecto al tiempo, se obtiene la aceleración am del punto m. La aceleración
am del punto m, en el caso general, se conforma de cuatro componentes: i) aceleración normal, dirigida a lo largo del
radio vector rm en dirección a su inicio; ii) aceleración tangencial, perpendicular al radio vector rm; iii) aceleración
relativa, dirigida a lo largo del radio vector rm; iv) aceleración de Coriolis, perpendicular al radio vector rm.
11.4
FACULTAD DE INGENIERÍA MECÁNICA – UNIVERSIDAD TECNOLÓGICA DE PEREIRA
am =
d vϕm
d vϕm d ϕ
d vm d
dω
= ( ω vϕm ) = ω
+ vϕm
=ω
+ vϕm α
dt
dt
dt
dt
dϕ d t
= ω2
d vϕm
dϕ
+ vϕm α = ω2 aϕm + vϕm α = ω2 r ''m + α r 'm
Las magnitudes ω2 y α poseen unidades rad/s2. La magnitud del análogo de velocidad vϕ tiene unidades de longitud.
d 2 rm
es el análogo de aceleración del punto m y también tiene unidades de longitud.
La magnitud aϕm = r ''m =
d ϕ2
Cuando el desplazamiento del eslabón k es rectilíneo, el análogo de su velocidad se representa mediante s 'k y el
análogo de su aceleración mediante s ''k
De esta manera las velocidades y aceleraciones de los eslabones, y de sus puntos pueden ser expresados siempre
mediante sus correspondientes análogos de velocidades y aceleraciones, y la velocidad y aceleración angular del
eslabón conductor. Si la ley de movimiento del eslabón conductor está dada en la forma s = s(t), donde s es el
desplazamiento lineal del eslabón inicial, entonces los análogos de velocidad y aceleración pueden ser hallados de
manera análoga.
Ya que los análogos de velocidades y aceleraciones dependen únicamente de la coordenada generalizada y no
dependen del tiempo, entonces el análisis cinemático del mecanismo puede ser realizado geométricamente. Si por
ejemplo, el eslabón conductor conforma un par giratorio, se gira en los ángulos ϕ y se determinan los
desplazamientos de los demás eslabones. Sí se requiere luego determinar las velocidades y aceleración del eslabón k
y sus puntos m, entonces se hallan los análogos de velocidades y aceleraciones ωϕ, αϕ, vϕ, aϕ; y se sustituyen en las
expresiones para las velocidades y aceleraciones previamente definidas.
11.3 DIAGRAMAS DE DESPLAZAMIENTO
Por lo común, un mecanismo leva-seguidor es un dispositivo con un grado de libertad. La leva es impulsada por un
movimiento de entrada conocida, casi siempre por un motor que gira a velocidad angular constante. La ley de
movimiento del seguidor, que depende de la coordenada generalizada de la leva, está condicionada por el proceso
tecnológico a cumplir. Durante un periodo de rotación de la leva, el seguidor ejecuta una serie de movimientos como
los que se muestran en el diagrama de desplazamientos de la Fig. 11.5.
s(ϕ)
subida
detenimiento
bajada
detenimiento
elevación
ϕ
Fig. 11.5. Diagrama de desplazamiento
Antes que se pueda determinar el contorno de la leva, es necesario elegir el movimiento con el requerimiento del
sistema.
Movimiento con velocidad uniforme
En la Fig. 11.6 se presenta un movimiento con velocidad constante. Este movimiento presenta aceleraciones infinitas
al inicio y al final del movimiento, por lo que actuarían fuerzas muy altas que generan golpes fuertes y vibraciones.
Es por esto que una ley de movimiento lineal se usa sólo entramos de las fases de retorno, y en la ley de movimiento
se introducen modificaciones en las transiciones de fase para suavizar la transición entro dos leyes de movimiento
lineales. Se puede realizar un redondeo por curvas tangentes, éste se hace en los puntos de inflexión un segmento de
circunferencia de radio r, Fig 11.9.b. Debe anotarse que el segmento lineal cambia entonces su pendiente. En la Fig
11.7.a y b se muestran los procedimientos necesarios para realizar esta ley.
11.5
LECCIÓN No 11. MECANISMO LEVA SEGUIDOR
s(ϕ)
lineal modificado
lineal
b
ϕ
k
a
lineal modificado
ϕ
C
D
A
r
lineal
s''(ϕ)
m
R
s'(ϕ)
B
E
r
h
R
ϕs - ϕs1
ϕs1
ϕs1
ϕs
+Q
ϕ
−Q
a) Ley de desplazamiento
b) construcción geométrica lineal modificado
Fig. 11.6 Movimiento lineal
Movimiento parabólico o de aceleración constante
El movimiento parabólico – Fig. 11.7– tiene la menor aceleración teórica para una elevación y una velocidad dada.
s(ϕ)
L
0
1
2
3
4
5
s(ϕ)
5
4
4
3
3
2
2
1
1
1
2
3
4
L
β
5 ϕ
β
a) Movimiento de aceleración
b) Movimiento de desaceleración
β3/2
s(ϕ)
L3
L3
L
L2
L1
L1
0
β
β1/2
β1
β2
β3
c) Velocidad constante modificado
Fig. 11.7 Movimiento parabólico
11.6
5
ϕ
ϕ
FACULTAD DE INGENIERÍA MECÁNICA – UNIVERSIDAD TECNOLÓGICA DE PEREIRA
El movimiento parabólico puede tener o no tener intervalos iguales de aceleración o desaceleración. Adicionalmente,
el movimiento parabólico puede modificarse para que incluya un intervalo de velocidad constante entre la
aceleración y la desaceleración; con frecuencia se denomina como velocidad constante modificada, Fig 11.7.c.
En la porción central de este movimiento, subtendido por el ángulo de giro de la leva β2 y elevación L2, es un
movimiento uniforme. En el diagrama se muestra como se deben igualar las pendientes del movimiento parabólico
con el de velocidad constante:
1) Conocidos los ángulos β1, β2 y β3 y la elevación total L: se traza la línea entre la sección media de aceleración
–β1– y de desaceleración –β3– y se determinan las elevaciones L1, L2 y L3.
2) Conocidas las elevaciones L1, L2 y L3 y el ángulo de giro de la leva β: se traza la línea entre la elevación –L1 al
inicio de la aceleración y L + L3 al final de la desaceleración y se determinan los ángulos de giro de la leva en
cada movimiento β1, β2 y β3.
Ley armónica
La Fig. 11.8 se presenta el movimiento armónico simple. La construcción gráfica utiliza una semicircunferencia con
diámetro igual a la elevación L. Es necesario dividir el eje de las abscisas en el número de partes en que se divide la
semicircunferencia y luego proceder tal como se muestra en la figura.
s(ϕ)
5'
4'
L
3'
2'
1'
0
1
2
3
4
5
6 ϕ
β
Fig. 11.8 Movimiento armónico simple
Ley Cicloidal
En la figura se presenta la construcción del movimiento cicloidal, esta ley debe su nombre a la cicloide que es la
trayectoria de un punto P de un círculo de radio r = L / 2π, siendo L la elevación, cuando gira sin deslizar sobre la
ordenada del diagrama de desplazamiento.
s(ϕ)
L
P
4'
3'
5'
0
2'
1
1'
2
3
0'
4
β
Fig. 11.9 Movimiento cicloidal
ϕ 1
ϕ
La expresión para el movimiento cicloidal es: s ( ϕ ) = L  − sin 2π 
β
 β 2π
11.7
5
6 ϕ
LECCIÓN No 11. MECANISMO LEVA SEGUIDOR
El diagrama se obtiene, de una manera más fácil, al ubicar el círculo en el origen del diagrama de desplazamiento,
dividir el círculo en un número de partes igual a la división de las abscisas del diagrama, obtener las proyecciones de
las divisiones sobre el eje de las ordenadas y trazar las líneas paralelas a la diagonal del diagrama de desplazamiento,
en la Fig. 11.9 se muestra este procedimiento.
En la literatura se encuentran gran cantidad de leyes y expresiones analíticas que permiten el cálculo del
desplazamiento y sus derivadas para cualquier posición del ángulo de fase. En las Fig. 11.10, 11.11 y 11.12 se
presentan las leyes propuestas por Kloomok y Muffley basadas en tres funciones analíticas: a) polinomio de octavo
grado b) cicloide y semicicloide, y c) armónica y semiarmónica.
s(ϕ)
L
2
5
6
7
8

ϕ
ϕ
ϕ
ϕ
ϕ 
= 6,09755   − 20,7804   + 26, 73155   −13, 60965   + 2,56095   
L

β
β
β
β
 β  
s ( ϕ)
ϕ
s'(ϕ)
β
4
5
6
7

ϕ
ϕ
ϕ
ϕ
ϕ 
s ( ϕ ) = L 12,1951  − 103,902   + 160,3893   −95, 26755   + 20, 4876   

β
β
β
β
 β  
ϕ
s''(ϕ)
ϕ
3
4
5
6

ϕ
ϕ
ϕ
ϕ 
s '' ( ϕ ) = L 12,1951 − 415, 608   + 801,9465   −571, 6053   + 143, 4132   

β
β
β
 β  
s(ϕ)
L
2
5
6
7
8

ϕ
ϕ
ϕ
ϕ
ϕ 
= 1 − 2, 63415   + 2, 78055   + 3,1706   −6,87795   + 2,56095   
L

β
β
β
β
 β  
s ( ϕ)
ϕ
β
s'(ϕ)
ϕ
s ' ( ϕ)
L
4
5
6
7

ϕ
ϕ
ϕ
ϕ
ϕ 
=  −5, 2683   + 13,90275   + 19, 0236   −48,14565   + 20, 4876   

β
β
β
β
 β  
s''(ϕ)
ϕ
s '' ( ϕ )
L
3
4
5
6

ϕ
ϕ
ϕ
ϕ 
=  −5, 2683 + 55, 611  + 95,118   −288,8739   + 143, 4132   

β
β
β
 β  
Fig. 11.10 Ley de desplazamiento polinomial de octavo orden
11.8
FACULTAD DE INGENIERÍA MECÁNICA – UNIVERSIDAD TECNOLÓGICA DE PEREIRA
C-1
C-2
s(ϕ)
s(ϕ)
L
L
ϕ 1
ϕ
s ( ϕ ) = L  − sin π 
β
β π
ϕ
s'(ϕ)
ϕ
β
s'(ϕ)
s ' ( ϕ) =
β
ϕ
L
 1 − cos π 
β
β
s ' ( ϕ) =
s''(ϕ)
s '' ( ϕ ) =
ϕ
L
 1 + cos π 
β
β
ϕ
ϕ
ϕ
s''(ϕ)
ϕ 1
ϕ
s ( ϕ ) = L  + sin π 
β
β π
πL
ϕ
sin π
2
β
β
s '' ( ϕ ) = −
πL
ϕ
sin π
2
β
β
ϕ
C-3
s(ϕ)
C-4
s(ϕ)
L
β
L
 ϕ 1
ϕ
s ( ϕ ) = L 1 − + sin π 
β
 β π
ϕ
ϕ
β
s'(ϕ)
ϕ
s'(ϕ)
ϕ
L
s ' ( ϕ ) = −  1 − cos π 
β
β
ϕ
ϕ
s''(ϕ)
 ϕ 1
ϕ
s ( ϕ ) = L 1 − − sin π 
β
 β π
L
ϕ
s ' ( ϕ ) = −  1 + cos π 
β
β
s''(ϕ)
s '' ( ϕ ) =
πL
ϕ
s '' ( ϕ ) = − 2 sin π
β
β
πL
ϕ
sin π
β
β2
ϕ
C-5
C-6
s(ϕ)
s(ϕ)
L
β
L
ϕ 1
ϕ
s ( ϕ ) = L  − sin 2π 
β
2
π
β

 ϕ 1
ϕ
s ( ϕ) = L 1 − +
sin 2π 
β
2
π
β

ϕ
ϕ
s'(ϕ)
s'(ϕ)
s ' ( ϕ) =
β
ϕ
L
ϕ
1 − cos 2π 
β
β
s ' ( ϕ) = −
L
ϕ
1 − cos 2π 
β
β
ϕ
s''(ϕ)
s''(ϕ)
ϕ
ϕ
2π L
ϕ
s '' ( ϕ ) = 2 sin 2π
β
β
s '' ( ϕ ) = −
Fig. 11.11 Características del movimiento cicloide
11.9
2π L
ϕ
sin 2π
2
β
β
LECCIÓN No 11. MECANISMO LEVA SEGUIDOR
H-1
H-2
s(ϕ)
s(ϕ)
L
ϕ
s'(ϕ)
L

πϕ 
s ( ϕ ) = L 1 − cos

2β 

β
s ( ϕ ) = L sin
ϕ
s'(ϕ)
β
πL
πϕ
sin
2β
2β
s ' ( ϕ) =
ϕ
ϕ
s''(ϕ)
π2 L
πϕ
cos
2
2β
4β
s '' ( ϕ ) =
ϕ
πL
πϕ
cos
2β
2β
s ' ( ϕ) =
ϕ
s''(ϕ)
πϕ
2β
s '' ( ϕ ) = −
H-3
π2 L
πϕ
sin
2β
4β2
H-4
s(ϕ)
s(ϕ)
L
s ( ϕ ) = L cos
L
πϕ
2β
ϕ
ϕ
β
β
s'(ϕ)
s'(ϕ)
ϕ
πL
πϕ
s ' ( ϕ) = −
sin
2β
2β
ϕ
ϕ
s''(ϕ)

πϕ 
s ( ϕ ) = L 1 − sin

2β 

s ' ( ϕ) = −
πL
πϕ
cos
2β
2β
s''(ϕ)
s '' ( ϕ ) = −
π2 L
πϕ
cos
2β
4β2
s '' ( ϕ ) =
ϕ
H-5
s(ϕ)
π2 L
πϕ
sin
2
2β
4β
H-6
s(ϕ)
L
s ( ϕ) =
L
L
πϕ 
1 − cos

2
β 
s ( ϕ) =
ϕ
L
πϕ 
1 + cos

2
β 
ϕ
β
s'(ϕ)
β
s'(ϕ)
s ' ( ϕ) =
πL
πϕ
sin
β
2β
ϕ
s''(ϕ)
s''(ϕ)
ϕ
s '' ( ϕ ) =
πL
πϕ
sin
β
2β
s '' ( ϕ ) = −
π2 L
πϕ
cos
β
2β2
ϕ
ϕ
π2 L
πϕ
cos
β
2β2
Fig. 11.12 Características del movimiento armónico
11.10
s ' ( ϕ) = −
FACULTAD DE INGENIERÍA MECÁNICA – UNIVERSIDAD TECNOLÓGICA DE PEREIRA
Ejemplo 11.1
Se desea diseñar una leva en el que el seguidor tenga un reposo desde la posición inicial durante 40° de rotación de la
leva. En el movimiento de ascenso durante 150° de rotación de la leva, se debe tener un movimiento con velocidad
constante durante 20 mm de elevación. Finalizado el movimiento de ascenso, se requiere un detenimiento del
seguidor durante 50° de rotación de la leva. El descenso se requiere un movimiento de descenso inicial de 18 mm
durante 40° de rotación de la leva, seguido de un detenimiento durante 40° de rotación de la leva, finalmente se tiene
el descenso de 15 mm en los 40° de rotación restantes de la leva. En la Figura 11.13 se presenta los movimientos
principales requeridos del seguidor en función de la rotación de la leva.
Se requiere elegir los movimientos adecuados para presentar continuidad de la ley de desplazamiento hasta la
segunda derivada. Determine los intervalos de las tres fases del movimiento de ascenso para garantizar la
continuidad.
Si la velocidad angular de la leva es ωL = 30 rad/s, determine las velocidades y aceleraciones máximas del seguidor.
s(ϕ) [mm]
8
18
20
15
5
ϕ [rad]
40°
150°
50°
40°
40°
40°
Figura 11.13 Ley de desplazamiento
Para la construcción adecuada del perfil, se requiere construir el análogo de velocidades y aceleraciones, con las
leyes definidas hasta el momento. De las figuras 11.10 a 11.12 se elegirán los movimientos adecuados para
garantizar la continuidad.
Observando las opciones para generar la ley de desplazamiento del seguidor en los intervalos faltantes, se eligen los
siguientes movimientos: i) en el ascenso inicial se elige la curva C1, ii) en el ascenso final se elige C2, iii) en el
descenso inicial y final se elige la curva C6.
Se requiere determinar los ángulos β1, β2, y β3, los cuales se obtienen de la condición de continuidad. La primera
ecuación se obtiene de la condición del diagrama de desplazamiento
β1 +β2 +β3 = 150 π /180
La condición de continuidad en el punto B se obtiene al evaluar el análogo de velocidades de la curva C1 en la fase
final, con el análogo de velocidades en el tramo con velocidad constante.
s1 ' ( ϕ1 ) =
L1 
ϕ1 
1 − cos π  , siendo ϕ1 = ϕ − β0
β1 
β1 
El cambio de variable se debe a que la expresión del análogo de velocidades son tomadas a partir del punto C.
Evaluando esta función en ϕ1 = β1 , se obtiene
s1 '(C) =
2 L1 L2
=
β1
β2
11.11
LECCIÓN No 11. MECANISMO LEVA SEGUIDOR
s(ϕ) [mm]
E
L3
F
D
L5
G
H
L2
C
A
L1
L7
B
β0
s'(ϕ) [mm/rad]
A
β1
β2
β3
β4
β5
β6
β7
2π
β1
β2
β3
β4
β5
β6
β7
2π
β1
β2
β3
β4
β5
β6
β7
2π
ϕ [rad]
L2/β2
0
β0
ϕ [rad]
s''(ϕ) [mm/rad2]
0
β0
Figura 11.14 Diagramas de desplazamiento y sus derivadas
Reemplazando los valores de los desplazamientos, se obtiene
β1 =
2 L1
β2 = 0,5 β2
L2
El análogo de velocidades de la curva C2 es:
L 
ϕ 
s3 ' ( ϕ ) = 3 1 + cos π 3  , siendo ϕ3 = ϕ − (β0 + β1 + β2 )
β3 
β3 
Evaluando esta función en el inicio φ3 = 0, que se corresponde con el punto D, se obtiene:
s3 '(D) =
2 L3 L2
=
β3
β2
Reemplazando los valores de los desplazamientos, se obtiene
β3 =
2 L3
β2 = 0,8 β2
L2
Reemplazando β1 y β3 en función de β2 se obtiene:
2,3 β2 = 150 π /180 rad;
β2 =1,1383 rad
β1 = 0,5691 rad
β3 = 0,9106 rad
Las ecuaciones para el movimiento de descenso son:
11.12
ϕ [rad]
FACULTAD DE INGENIERÍA MECÁNICA – UNIVERSIDAD TECNOLÓGICA DE PEREIRA
 ϕ
ϕ 
1
s5 ( ϕ ) = L7 + L5  1 − 5 +
sin 2π 5  , siendo ϕ5 = ϕ − (β0 + β1 + β2 + β3 + β4 )
β
2
π
β5 

5
 ϕ
ϕ 
1
s7 ( ϕ ) = L7  1 − 7 +
sin 2π 7  , siendo ϕ7 = ϕ − (2π − β7 )
β7 
 β7 2 π
Las ecuaciones de los análogos de velocidades y aceleraciones, se obtienen de manera muy similar a las leyes de
desplazamiento. En La figura 11.15 se representan el diagrama de desplazamiento del seguidor y su primera y
segunda derivada.
s(ϕ) [mm]
40
C2
C6
20
C6
C1
ϕ [rad]
0
0
s'(ϕ) [mm/rad]
1
2
3
4
5
6 2π
7
40
20
0
-20
ϕ [rad]
0
1
2
3
4
5
6
2π
7
-40
-60
s''(ϕ) [mm/rad2]
300
0
ϕ [rad]
0
1
2
3
4
5
6
2π
7
-300
Figura 11.15
Del diagrama cinemático se observa que los mayores valores del análogo de velocidades y de aceleraciones se
presentan en el primer movimiento de descenso. El máximo valor del análogo de velocidad se obtiene para
ϕ5 = β5 / 2 , en el análogo de aceleraciones se presenta en ϕ5 = β5 / 4 , y en ϕ5 = 3 β5 / 4 .
El máximo valor del análogo de velocidades se obtiene mediante:
s5 ' ( ϕ ) = −
ϕ5 
L5 
 1 − cos 2π 
β5 
β5 
s ' ( ϕ )máx = s5 ' ( ϕ5 = β5 / 2 ) = −
2 L5
= −51,5662 mm/rad
β5
Para obtener el valor de la velocidad del seguidor, se multiplica por la velocidad angular de la leva:
vmáx = ωL ⋅ s 'máx = 30 rad/s ⋅ 51,5662 mm/rad = 1,547 m/s
La máxima velocidad se obtiene en el descenso del seguidor.
De manera similar se evalúa el análogo de aceleraciones
11.13
LECCIÓN No 11. MECANISMO LEVA SEGUIDOR
s5 '' ( ϕ ) = −
2π L5
s ''máx = s5 '' ( ϕ = β5 / 4 ) = −
β52
sin 2π
2π L5
β52
ϕ5
β5
= −232, 0479 mm/rad 2
La máxima aceleración se obtiene mediante:
2
amáx = ωL2 ⋅ s ''máx = ( 30 rad/s ) 232, 0479 mm/rad 2 = 208,84 m/s 2
11.4 DISEÑO GRÁFICO DEL PERFIL DE LAS LEVAS
Una vez elegido la ley de movimiento deseado del seguidor, la tarea consiste en obtener el perfil apropiado de la leva
para lograr el movimiento del seguidor representado en el diagrama de desplazamiento.
El diseño gráfico del perfil de la levas se basa en el proceso de inversión del mecanismo leva-seguidor, en el que la
leva se considera fija y la guía o articulación del seguidor móvil. La inversión cinemática no afecta los movimientos
relativos entra la leva y el palpador. El perfil de la leva es el haz de curvas correspondientes con las distintas
posiciones del palpador del seguidor en una vuelta de la leva.
Para claridad del procedimiento, se hace necesario establecer una nomenclatura adicional basada en la Fig 11.16.
El punto de trazo es un punto teórico del seguidor; corresponde al punto de un seguidor puntual o el centro del
rodillo en esta clase de seguidor.
La curva de paso es el lugar geométrico generado por el punto de trazo conforme el seguidor se mueve en relación
con la leva. Para un seguidor puntual, la curva de paso y la superficie de la leva son idénticas. En el caso de un
seguidor de rodillo, están separadas por el radio de rodillo.
La circunferencia primaria es la más pequeña que se puede trazar con centro en el eje de rotación de la leva y
tangente a la curva de paso. El radio de esta circunferencia es R0.
La circunferencia base es la circunferencia más pequeña con centro en el eje de rotación de la leva y tangente a la
superficie de ésta. En el caso de un seguidor de rodillo, la diferencia entre la circunferencias base y primaria es el
radio de rodillo, en el caso de un seguidor de cara plana o seguidor puntual, son idénticas.
11.4.1 LEVA DE DISCO CON SEGUIDOR DE RODILLO CON MOVIMIENTO DE TRASLACIÓN
El perfil de la leva se obtiene basado en la ley de desplazamiento del seguidor deseado –Fig 11.16.a. El
procedimiento gráfico de obtención del perfil de la leva –Fig 11.16.b– es el siguiente:
1.
Dividir cada uno de las fases de movimiento en un número de partes iguales, en la ley de desplazamiento del
seguidor considerada, se tienen cuatro fases: i) un movimiento de subida durante 120º de giro de la leva, se
utiliza en este caso una ley armónica, ii) un movimiento de detención durante 60º de giro de la leva, iii) un
movimiento de bajada durante 120º de giro de la leva, iv) movimiento de detención durante 60º de giro de la
leva. El primer y tercer movimiento se dividen, en este ejemplo, en seis partes iguales.
2.
Elegir el centro de rotación de la leva, punto A de la Fig 11.16.b, con centro en A trazar la circunferencia base
de la leva con radio Rb –parámetro de diseño previamente definido– y dibujar la circunferencia primaria de radio
R0 = Rb + Rr, siendo este último el radio del rodillo. Dividir el círculo base en las respectivas fases de
movimiento, en cada fase representar las líneas radiales correspondientes con las divisiones realizadas en el
diagrama de desplazamiento. En la primera fase, correspondiente con una subida del seguidor, se tiene 7 líneas
radiales distribuidas uniformemente en 120º de rotación de la leva. Entre 180º y 300º se tiene el movimiento de
bajada en el que se tienen otras 7 líneas radiales correspondientes con las posiciones 8 a la 14.
3.
Transferir los desplazamientos s(ϕ1), s(ϕ2), etc del diagrama de desplazamiento del palpador a las líneas radiales
correspondientes, midiendo desde la circunferencia primaria. El lugar geométrico de cada una de las posiciones
del punto de trazo, punto B del rodillo, se conoce como curva de paso.
11.14
FACULTAD DE INGENIERÍA MECÁNICA – UNIVERSIDAD TECNOLÓGICA DE PEREIRA
120º
subida
60º
det.
120º
bajada
60º
det.
7,8
6,9
5,10
4,11
rotación
de la leva
elevación
3,12
2,13
2
B
1,14
1 2 3 4 5 6 7
3
8
9 10 11 12 13 14
1 ϕ
a) Ley de desplazamiento
4
14
iv
5
13
i
A
12
6
iii
ii
11
R0
Rb
circunferencia
primaria
circunf.
base
10
7
curva de paso
b) Perfil de la leva
9
8
Fig 11.16 Perfil de la leva de disco con seguidor de rodillo
4.
Representar el rodillo sobre cada una de las líneas radiales en cada una de las posiciones que correspondan, el
rodillo se representa mediante una circunferencia de radio Rr. El perfil de la leva se obtiene como la curva que es
tangente a cada uno de las circunferencias que representa el rodillo. El perfil de la leva se puede obtener como la
curva offset de la curva de paso, la distancia entre ambas curvas es dada por el radio del rodillo.
11.4.2 LEVA DE DISCO CON SEGUIDOR DE RODILLO CON MOVIMIENTO DE TRASLACIÓN,
EXCÉNTRICO
En la Fig 11.17 se presenta el procedimiento para un seguidor de rodillo excéntrico.
1.
Dividir cada una de las fases de movimiento de la ley de desplazamiento en un número de partes iguales. En este
caso se consideran dos fases: i) movimiento de subida con ley armónica en un ángulo de rotación de la leva de
180º, ii) movimiento de descenso con ley armónica en los restantes 180º de rotación de la leva.
2.
Elegir el centro de rotación de la leva, punto A, con centro en A trazar la circunferencia de excentricidad con
radio e, la excentricidad es un parámetro de diseño. Trazar la circunferencia primaria con radio R0, parámetro de
diseño del perfil de la leva. Trazar la línea vertical que representa el movimiento del seguidor. Representar el
punto B1 en el punto de corte de la circunferencia primaria con la línea del movimiento del seguidor.
3.
Dividir la circunferencia de excentricidad en el mismo número de divisiones del diagrama de desplazamiento del
seguidor. Trazar tangentes en cada una de las divisiones de esta circunferencia.
4.
Transferir los desplazamientos s(ϕ1), s(ϕ2), etc., del diagrama de desplazamiento sobre la correspondiente línea
tangente medidas desde la circunferencia de paso. La curva de paso es el lugar geométrico de todos los puntos
de trazo obtenidos.
11.15
LECCIÓN No 11. MECANISMO LEVA SEGUIDOR
7
6,8
5,9
e
4,10
3,11
2,12
1
12
11
1
2
2
3
4
5
6
7
8
9
10
11
12
1
a) Ley de desplazamiento
10
9 10
8
A
7
11
12
1
3
2
6
5
9
4
3
4
círcunf. de
excentricidad
R0
círcunf.
primaria
8
rotación
de la leva
5
curva de paso
b) Perfil de la leva
6
7
Fig. 11.17 Perfil de la leva de disco con seguidor de rodillo
5.
Representar el rodillo sobre cada una de las líneas radiales en cada una de las posiciones que correspondan, el
rodillo se representa mediante una circunferencia de radio Rr. El perfil de la leva se obtiene como la curva que es
tangente a cada uno de las circunferencias que representa el rodillo. El perfil de la leva se puede obtener como la
curva offset de la curva de paso, la distancia otra ambas curvas es dada por el radio del rodillo.
11.4.3 LEVA DE DISCO CON SEGUIDOR DE CARA PLANA
En la Fig. 11.18 se presenta el procedimiento para generar el perfil de la leva a partir de la ley de desplazamiento del
seguidor.
1.
Seleccionar un punto A, con centro en este punto dibujar la circunferencia base de la leva. Dividir la
circunferencia base en el mismo número de divisiones de la ley de desplazamiento del seguidor. Estas divisiones
están acordes con las fases de movimiento deseadas para el seguidor. Trazar líneas radiales por cada división de
la curva base.
2.
Dibujar el seguidor en la posición inicial tangente a la circunferencia base.
3.
Transferir los desplazamientos s(ϕ1), s(ϕ1), etc., desde el diagrama de desplazamiento a las líneas radiales
correspondientes midiendo desde la circunferencia base y trazar líneas perpendiculares a las líneas radiales en
los puntos correspondientes. Cada línea perpendicular representa la cara de contacto del seguidor con la leva.
4.
Trazar una curva suave tangente a cada una de las caras del seguidor dibujadas, esta curva representa el perfil de
la leva.
11.16
FACULTAD DE INGENIERÍA MECÁNICA – UNIVERSIDAD TECNOLÓGICA DE PEREIRA
1
2
16
3
15
Rmín
4
14
ω1
5
13
6
12
11
7
8
9
10
90º
Fig 11.18 Perfil de la leva de disco con seguidor plano
11.4.4 LEVA DE DISCO CON SEGUIDOR DE RODILLO CON MOVIMIENTO DE ROTACIÓN
Una vez elegida la ley de desplazamiento del seguidor, θ(ϕ), y después de determinar el radio de la circunferencia
base, se procede a generar el perfil de la leva. El procedimiento para la generación del perfil de la leva, que es
mostrado en la figura 11.19, es el siguiente:
1. Elegir el centro de rotación de la leva, elegir la circunferencia primario de radio R0 = Rb + Rr.
2. Ubicar el centro de rotación del seguidor en O2, trazar la circunferencia con centro en O1 y con radio O1O2 y
ubicar en ésta los puntos pivotes de la intersección de las líneas radiales con esta circunferencia, 1′, 2′, etc.
3. Determinar la primera posición del seguidor del rodillo.
4. Medir mediante líneas radiales los desplazamientos angulares del seguidor θ(ϕ) desde su primera posición
angular.
5. Desde los puntos pivote 1′, 2′, 3′, etc., se trazan arcos con radio igual a la longitud del balancín LO2B
6. Con centro O1 se describen los arcos que pasan por las distintas posiciones del centro del rodillo en su
trayectoria. Los puntos de intersección de estos arcos con los arcos correspondientes trazados desde los puntos
pivote 1′, 2′, 3′, etc., determinan la curva de paso. Dibujar en estos puntos de corte, una circunferencia con radio
igual al del rodillo, Rr.
7. Trazar una curva suave tangente a cada una de las posiciones del seguidor dibujada. Esta curva es el perfil
aproximado de la leva.
11.17
LECCIÓN No 11. MECANISMO LEVA SEGUIDOR
10
9
11
7
6,8
12
8
12
11
3,11
10
5,9
4,10
2,12
1
rotación
de la leva
2
9
1
7
3
R0
8
4
círculo
primario
2
6
7
5
6
curva de paso
3
5
4
Fig. 11.19 Leva de disco con seguidor de rodillo con movimiento de rotación
11.4.5 LEVA DE DISCO CON SEGUIDOR PLANO CON MOVIMIENTO DE ROTACIÓN
En la figura 11.2º se muestra el procedimiento para la construcción de una leva con seguidor de cara plana con
movimiento de traslación. El ángulo de rotación del seguidor es de 20°. El desplazamiento angular del seguidor
contempla tres fases: i) rotación de 20° del seguidor durante una rotación de la leva de 150° mediante una función
armónica, ii) reposo del seguidor durante los 60° siguientes, y iii) retorno del seguidor en los 150° finales siguiendo
una ley armónica. El procedimiento de construcción del perfil de la leva es el siguiente:
1) Ubique el centro de rotación de la leva. Trace la circunferencia primaria con radio R0, ubique al seguidor a un
radio AB, ubique el centro de rotación del seguidor. Trace la circunferencia de radio R en el centro de rotación
del seguidor. La línea CP define la línea de contacto entre la leva y el seguidor. La línea CP es tangente a la
circunferencia de radio R. El punto P es un punto auxiliar, ubicada sobre la línea de la cara del seguidor, que
permite construir el perfil de la leva.
2) Con radio OP construya el movimiento deseado del seguidor durante las fases de movimiento. Para esto
determine las posiciones límite del punto P cuando el seguidor gira los 20° definidos. Sobre la línea entre los
puntos límites, construya la ley de desplazamiento deseada
3) Trace la circunferencia con centro en A y radio AB, está permite ubicar a los centros del seguidor en el
mecanismo inverso. Defina las tres fases de movimiento de la ley de desplazamiento, en sentido contrario a la
rotación de la leva. Divida las fases en el número de divisiones utilizado para construir la ley de desplazamiento,
para este caso 6 divisiones.
4) La ubicación del seguidor en el mecanismo inverso se obtiene mediante dos arcos. El primero es el arco con
centro A y radio igual AP; el segundo es con centro en correspondiente punto B, centro de rotación del seguidor
en el mecanismo inverso, y radio BP. Ejemplo P3 se encuentra en el corte de los arcos con radio AP3 y centro A,
y el arco con centro en B3 y radio BP.
11.18
FACULTAD DE INGENIERÍA MECÁNICA – UNIVERSIDAD TECNOLÓGICA DE PEREIRA
6,7
5,8
11
10
4,9
12
6,7
5,8
3,10
4,9
3,10
2,11
9
1,12
0
R
20°
2,11
B
0
1,12
0P
P3
C
C8
8
Fase III
1
R0
A
7
Fase II
Fase I
2
C3
ω
3
C6
P8
P6
4
6
5
Figura 11.20 Seguidor de cara plana con movimiento de rotación
5.
6.
Desde P3 trace la línea tangente a la circunferencia con centro en B3 y radio R. La línea P3C3 define el contacto
entre la leva y el seguidor. En la figura 11.20, se muestra adicionalmente el procedimiento para las posiciones 6
y 8.
Determine todas las líneas de contacto entre la leva y el seguidor y trace el perfil de la leva como la curva que es
tangente a estas líneas.
11.5 EL ÁNGULO DE PRESIÓN
En la Fig. 11.21 se presenta dos eslabones con transmisión por contacto en el punto C; la dirección de la fuerza de
contacto entre los eslabones es en la dirección de la normal de las superficies del punto de contacto. El ángulo φ
formado por la dirección de la acción de la fuerza F aplicada al eslabón conducido y la velocidad vc2 del punto de
contacto perteneciente al mismo eslabón –conducido, se llama ángulo de presión.
11.19
LECCIÓN No 11. MECANISMO LEVA SEGUIDOR
d34
4
K1
n
t
1
T
3
K2
2
2
C(C1,C2)
B
ω2
ω1
A
ω1
B
vc2c1
t
F
γ12
φ
vc2
P
φ
S
1
A
n
a) Superficies en contacto
b) Mecanismo leva seguidor
Fig 11.21 Definición del ángulo de presión
Con el fin de aumentar la fuerza útil T y disminuir la fuerza S es conveniente que el ángulo de presión sea lo más
pequeño posible. Si la fuerza S es muy alta, que se presenta para ángulos de presión altos, el seguidor es empujado
hacia la guía con tendencia a bloquear su movimiento.
La ecuación de velocidades del mecanismo equivalente es:
d34
4
vB = vM + vBM
1
donde vM ⊥ AM , vB d34 , vBM ⊥ BM
P
3
φ
2
y
B
Trazando desde el apoyo A una línea perpendicular a d34 y
proyectando la línea BM, se encuentra el punto B′. Con este
punto se obtiene el triángulo AB′M semejante al plano de
velocidades pmb ya que sus lados son perpendiculares:
K
φ
b
vMB
M
ω
r
B'
y
A
∆ pmb (plano de velocidades) semejante ∆ A B′M
m
vB
vM
AB' y vB
= =
AM r vM
p
a) Cálculo del ángulo de presión
b) Velocidades
d s3
ds3
ds
dt
=
=
= 3
ω r r ω d t r dϕ
ds3
. Con la anterior expresión se obtiene la ubicación del punto K en función del análogo de
dϕ
velocidades de la ley de desplazamiento del seguidor. Trazando desde el punto B una línea perpendicular a d34 y de
magnitud igual a y, se encuentra el punto K. Trazando la línea AK, se cumple:
Por lo tanto y =
En cualquier posición del mecanismo, la línea AK forma con la perpendicular al análogo de velocidad –línea BK de
magnitud y– el ángulo de presión φ.
Los mecanismos de leva – seguidor deben ser diseñados tal que los valores máximos del ángulo de presión φmáx no
sean superiores a cierta magnitud. En la práctica, para un mecanismo leva seguidor, con movimiento rectilíneo del
seguidor φmáx = 30º; para un mecanismo leva seguidor, con movimiento oscilante del seguidor φmáx = 45º. Esta
condición puede ser satisfecha, para la ley de movimiento del seguidor, mediante la adecuada elección del radio de la
circunferencia primaria.
11.20
FACULTAD DE INGENIERÍA MECÁNICA – UNIVERSIDAD TECNOLÓGICA DE PEREIRA
s3
K
B
φ
s
B1
φ2
K2
K1
y1,máx
y2,máx
φ1
B2
s1
φ2,máx
φ1,máx
s2
Β0
y
r0
A
e
Fig. 11.22 Diagrama desplazamiento – análogo de velocidades
Para cada desplazamiento del seguidor s3, correspondiente con cada ϕ1, se calcula el valor del análogo de
velocidades y se consigna tal como se muestra en la Fig. 11.22. Uniendo todos los segmentos se obtiene la curva que
representa el diagrama s3, d s3 / d ϕ1. En este diagrama, si el análogo de velocidades es positivo se representa hacia la
derecha, si es negativo hacia la izquierda. En los mecanismos con cierre del par por fuerza, la parte izquierda no tiene
importancia, por representar el movimiento de descenso.
Del diagrama de desplazamiento – análogo de velocidades, es posible dimensionar el radio de la circunferencia
primitiva que satisface un ángulo de presión máximo entre la leva y el seguidor, ver Fig 11.23. Para esto es necesario
realizar lo siguiente:
s3
B1
y1,máx
s3,1
K1
φmáx
B0
y
ro
φmáx
ro,2
A
φmáx
A2
e
Fig 11.23 Diseño de la circunferencia primitiva
11.21
LECCIÓN No 11. MECANISMO LEVA SEGUIDOR
1. Encontrar el punto K1 en el que el análogo de velocidades s′, alcanza su valor máximo, y1,máx
2. En el punto K1 trazar la línea 1-1 formando el ángulo φmáx con la vertical.
3. En el punto B0 trazar la línea 2-2 formando el ángulo φmáx con la vertical en sentido contrario. La intersección de
las líneas 1-1 y 2-2, punto A, es el centro de la leva con menores dimensiones.
4. Esto determina la excentricidad de la leva, e, y el radio de la circunferencia primitiva, R0.
5. Si por razones constructivas, se requiere ubicar el centro de la leva en otro sitio, se ubica en la zona sombreada.
6. Para un mecanismo con seguidor radial, e = 0, el centro de la leva se ubica en A2.
Ejemplo 11.2
Determinar el radio de la circunferencia primitiva para un mecanismo de leva de disco y seguidor de rodillo,
excéntrico, Si se desea que el ángulo de presión máximo sea menor a 30 °. Se desea que el seguidor realice los
siguientes movimientos: i) una elevación de 25 mm durante 150° de rotación de la leva utilizando una ley cicloidal,
C1, ii) un reposo durante los siguientes 50° de rotación de la leva, iii) un descenso durante 120° de rotación de la
leva, utilizando la ley armónica, y iv) un detenimiento del seguidor en los 40° restantes.
En la figura 11.24 se presenta el diagrama de desplazamiento y el análogo de velocidades con las leyes de
movimiento propuesto.
s(ϕ) [mm]
25
20
15
10
5
ϕ [rad]
0
0
1
2
1
2
3
4
a) Ley de desplazamiento
5
6 2π
5
6 2π
s'(ϕ) [mm]
20
10
0
-10
-20
ϕ [rad]
0
3
4
b) análogo de velocidades
Figura 11.24 Ley de desplazamiento y su derivada del ejemplo 11.2
Definida la ley de desplazamiento y el análogo de velocidades, se construye el diagrama s(φ) vs s’(φ), este diagrama
se presenta en la figura 11.25. El vértice del diagrama s(φ) vs s’(φ), es la posición inferior del seguidor.
El punto k representa el punto en el que se obtiene el máximo valor del análogo de velocidades, en este punto se
trazan la línea formando el ángulo de presión con la vertical. En la figura se presenta esta solución marcada por el
círculo A’. Si se ubica el centro de la leva en esta posición, se tendría una circunferencia primitiva con radio
R0 = 5,94 mm, y una excentricidad e = 5,94 mm.
Sin embargo es preferible ubicar el centro de rotación de la leva con la línea tangente al diagrama s(φ) vs s’(φ),
ubicando el punto A. En esta configuración se tiene una circunferencia primitiva con radio R0 = 13 mm, y una
excentricidad e = 6,6 mm.
Determinada la ubicación del centro de rotación de la leva, se procede a obtener el perfil de la leva. El seguidor es un
seguidor de rodillo de 2,5 mm de radio, el sentido de rotación de la leva es en sentido horario. En la figura 11.26 se
presenta el procedimiento realizado.
11.22
FACULTAD DE INGENIERÍA MECÁNICA – UNIVERSIDAD TECNOLÓGICA DE PEREIRA
s [mm]
30
25
20
15
s'máx
k
10
5
0
-15
-10
-5
0
5
10
15
30°
s' [mm]
20
R0
30°
A'
A
e
Figura 11.25 Dimensionamiento de la circunferencia primitiva
Para obtener la ley de desplazamiento se divide los 360° en los cuatro intervalos requeridos: i) 150° movimiento de elevación con
ley cicloidal, ii) detenimiento en los 50°, iii) descenso en 120° de rotación de la leva, y iv) reposo en 40°. Los movimientos de
ascenso y descenso se dividen a la vez en seis partes iguales para generar la ley de movimiento.
Para la ley cicloidal se calcula el radio de la circunferencia tal que su perímetro sea igual a la elevación de 25 mm:
r=
L
25
=
= 3,98 mm
2π 2π
Esta circunferencia se divide también en seis partes iguales y se procede tal como se menciona anteriormente.
En el movimiento de descenso se traza el semicírculo con diámetro igual a la elevación, para generar el movimiento
armónico. Como se menciona anteriormente, este semicírculo se divide en el mismo número de partes que el
diagrama.
Se ubica la posición inferior del seguidor, y sobre el eje vertical se trazan los desplazamientos correspondientes con
la rotación de la leva. En el lado izquierdo se representan los movimientos de elevación y en el derecho los de
descenso.
Con el radio de la circunferencia primaria, y la excentricidad se ubica el apoyo fijo y se trazan la circunferencia
primaria y la circunferencia de excentricidad. Esta última se divide tal como se realizó con el diagrama de
desplazamiento: 6 divisiones en los 150 ° en sentido contrario a la rotación de la leva, 50° constantes, 6 divisiones en
los siguientes 120°. Se trazan las líneas perpendiculares a las líneas radiales, y se trazan los arcos con centro en el
apoyo A y radio desde el apoyo hasta la elevación del centro del rodillo requerida.
En los puntos de corte se ubica el rodillo y se encuentra la curva de paso, curva que pasa por los centros de los
rodillos, y el perfil de la leva, curva tangente a los rodillos o la curva paralela a la curva de paso
11.23
LECCIÓN No 11. MECANISMO LEVA SEGUIDOR
s(ϕ)
0
1
2
3
4
5
6
7
8 9 10 11 12 13
0 ϕ [rad]
s(ϕ)
6
5
7
8
4
9
3
10
2
11
1
0
1
13
12
13
2
12
11
12 11 10 9
13
8
3
10
7
0
1
2
3
4
5
6
9
4
8
5
7
6
Figura 11.26 Generación del perfil de la leva
.
11.24
FACULTAD DE INGENIERÍA MECÁNICA – UNIVERSIDAD TECNOLÓGICA DE PEREIRA
11.6 EL RADIO DE CURVATURA
El radio de curvatura es una propiedad inherente de una curva; generalmente una leva, tendrá un radio de curvatura
instantáneo diferente en cada punto de su perfil. El perfil de la leva es generalmente funciones de alto grado,
presentando en algunos casos perfiles cóncavos, convexos o planos.
El radio de curvatura de la leva tiene una gran importancia en su diseño que permite identificar la presencia de
características geométricas indeseadas que impiden un correcto contacto entre la leva y el seguidor. Se puede
presentar básicamente dos problemas:
1. Imposibilidad de acceso del seguidor al punto teórico de contacto a causa que el seguidor invade tramos de la
leva al intentar acceder a estos puntos. En este caso, el radio de rodillo es mayor que el radio cóncavo del perfil
de la leva, Fig 11.26.
leva
Rr
rmin
seguidor
Fig. 11.26 Tramos dobles en la superficie de la leva
2. Existencia de irregularidades del perfil de la leva. A pesar que la ley de desplazamiento sea continua y suave, es
posible que el perfil de la leva presente vértices, radios del rodillo igual al menor radio de curvatura de la leva
Fig 11.27.a, o autointerseccones, el radio del rodillo es mayor que el radio de curvatura mínimo de la leva
Fig 11.27.b. En el primer caso se forma una cúspide en el perfil de la leva; esta leva no se desplazará
adecuadamente.
curva de
paso
Rr
ρ
Rr
ρ
curva de
paso
superficie
de la leva
superficie
de la leva
a) radio del rodillo Rr = ρmín
b) radio del rodillo Rr > ρmín,
Fig 11.27 Irregularidades del perfil de leva
La determinación analítica de la curva de paso de una leva no presenta dificultades depende del análisis del radio de
curvatura. El radio de curvatura es función que depende de algunos parámetros como radio de la circunferencia de
paso, de la ley de desplazamiento, y de la excentricidad en el caso de los seguidores radiales de traslación o de la
posición angular de referencia del seguidor si el movimiento es de rotación. En la expresión del radio de la curva de
paso, la única variable es, por ende, el ángulo de giro de la leva.
R = R ( ϕ)
El radio de curvatura de la curva de paso se define mediante:
11.25
LECCIÓN No 11. MECANISMO LEVA SEGUIDOR
R ( ϕ ) = R0 + s ( ϕ )
Para la leva con seguidor de movimiento de traslación y radial, el radio de curvatura es dado por:
ρP =
 R 2 ( ϕ ) + ( s ' ( ϕ ) )2 


2
3/ 2
R 2 ( ϕ ) + 2 ( s ' ( ϕ ) ) − R ( ϕ ) s '' ( ϕ )
donde s(ϕ) es la ley de desplazamiento del seguidor.
11.26