Primer parcial 09 - letra y sol
Anuncio
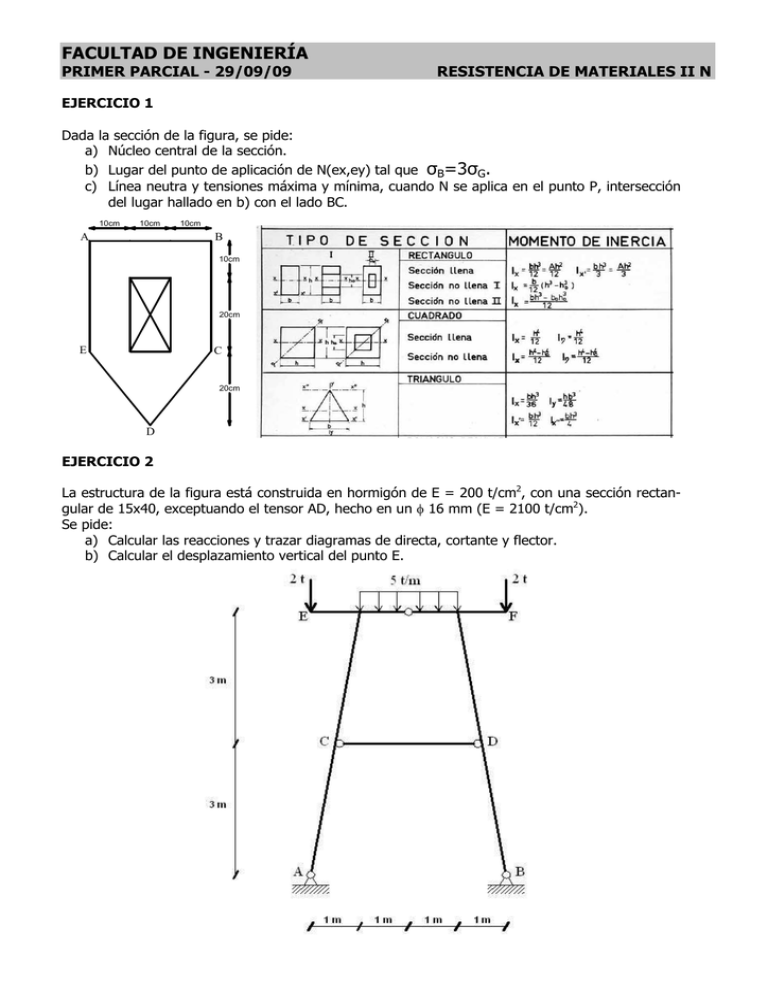
FACULTAD DE INGENIERÍA PRIMER PARCIAL - 29/09/09 RESISTENCIA DE MATERIALES II N EJERCICIO 1 Dada la sección de la figura, se pide: a) Núcleo central de la sección. b) Lugar del punto de aplicación de N(ex,ey) tal que σB=3σG. c) Línea neutra y tensiones máxima y mínima, cuando N se aplica en el punto P, intersección del lugar hallado en b) con el lado BC. 10cm 10cm A 10cm B 10cm 20cm E C 20cm D EJERCICIO 2 La estructura de la figura está construida en hormigón de E = 200 t/cm2, con una sección rectangular de 15x40, exceptuando el tensor AD, hecho en un φ 16 mm (E = 2100 t/cm2). Se pide: a) Calcular las reacciones y trazar diagramas de directa, cortante y flector. b) Calcular el desplazamiento vertical del punto E. PREGUNTA 1 – Segundo teorema de Castigliano a) Enunciar el teorema, indicando las hipótesis sobre las características de la estructura. b) Enunciar sin demostrar las propiedades de las matrices K y F que son necesarias para demostrar el teorema. c) Demostrar el teorema aceptando las hipótesis sobre la estructura y las propiedades indicadas en b). d) Mostrar cómo se puede aplicar el teorema para resolver una estructura hiperestática (cuya hiperestaticidad esta generada por apoyos redundantes). e) Generalizar al caso de un reticulado hiperestático (cuya hiperestaticidad esta producida por una barra redundante). Enunciar como se procede y demostrar. PREGUNTA 2 – Núcleo central a) Enunciar el sentido físico del núcleo central para una viga de sección cualquiera. b) Partiendo de la expresión σ= N e x x e y y 1+ 2 + 2 , A ρ y ρ x indicar qué expresa y qué son cada uno de sus términos. c) Definir una correspondencia biunívoca entre los puntos de aplicación de la fuerza y la línea neutra correspondiente, indicando los conjuntos entre los que se define esa correspondencia. Mostrar que la anterior es una correspondencia biunívoca. d) Mostrar que los puntos de aplicación, correspondientes a tres líneas neutras paralelas, están alineados y que esa recta pasa por el baricentro de la sección. e) Hallar el núcleo central de una sección rectangular de altura h y espesor b, explicando el razonamiento (enunciando y dando por validas, sin demostrar, las propiedades generales de la correspondencia biunívoca que sea necesario utilizar).








