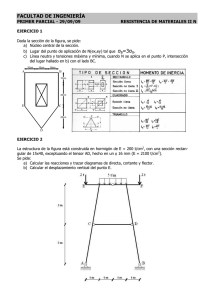
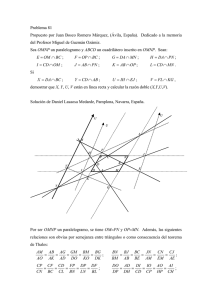
Relación de Problemas. Geometrıa Proyectiva 1. Teorema X
Anuncio

Relación de Problemas. Geometrı́a Proyectiva 1. Teorema X. Consideramos dos cuadrilateros ABCD A0 B 0 C 0 D0 en el plano proyectivo cuyos vértices están alternativamente sobre dos rectas distintas r y s. Si los puntos de corte de tres de los pares de lados homólogos A ∨ B ∩ A0 ∨ B 0 , B ∨ C ∩ B 0 ∨ C 0 y C ∨ D ∩ C 0 ∨ D0 están sobre una recta t, entonces el punto de corte del otro par de lados homólogos D ∨ A ∩ D0 ∨ A0 está tambien sobre la recta t. 1) Enunciar la versión afı́n del Teorema X cuando t es la recta del infinito. 2) Enunciar el teorema dual del Teorema X. 3) Enunciar la versión afı́n del teorema dual del Teorema X para el caso en el que los cuadriláteros sean paralelogramos. 4) Demostrar el Teorema X.