analisis combinatorio
Anuncio

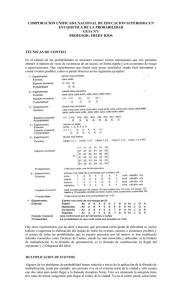
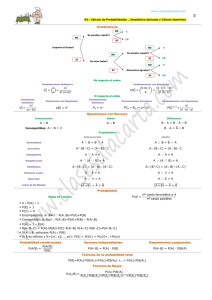
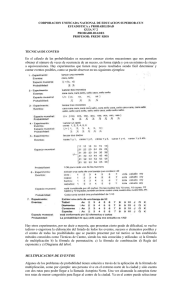
1 Universidad de San Carlos de Guatemala Centro Universitario de Occidente División Ciencias de la Salud Carrera de Médico y Cirujano, Primer Año, 2016 Teléfonos: 78730000, EXT. 2227- 2221-2244 CUNOC-USAC CURSO DE BIOESTADISTICA Semana 6 ANALISIS COMBINATORIO Orientado al estudio de las probabilidades, el análisis combinatorio o análisis del numero de formas en las que pueden presentarse los resultados de un proceso, ayuda a cuantificar la probabilidad de que ocurra un resultado en particular. El análisis combinatorio tiene como elementos fundamentales las permutaciones y las combinaciones. Estos elementos se estudian en este capitulo. PERMUTACIONES Una permutación es una forma en la que pueden presentarse los objetos o eventos y, en la que el orden de aparición es muy importante, por ejemplo: los dígitos 2, 5 y 8 pueden formar los números 258, 285, 528, 582, 825 y 852. Cada uno de ellos es una permutación de los dígitos 2, 5 y 8, y refleja valores muy diferentes entre si. Lo mismo puede decirse de las letras A, V y E: AVE, EVA y VEA son palabras diferentes. La fórmula general de las permutaciones es la siguiente: _____________________ Permutaciones de n objetos tomados de r en r ______________________ = nPr n! _______________________ = (n - r ) n es el número total de objetos o eventos r es el número de objetos que se desea considerar (n puede ser cualquier valor entero positivo; r puede ser cualquier valor entero positivo desde 1 hasta n) ! PERMUTAR ALGUNOS OBJETOS, DE TODOS DIFERENTES: El número de formas diferentes en que pueden ordenarse n objetos diferentes cuando se toman algunos de éstos (r), es el número de permutaciones, tal como se ejemplifica a continuación: EJERCICIOS En una caja hay cuatro canicas (azul, negra, roja y verde) Si se extraen de la caja dos de ellas ¿en qué orden pueden aparecer? SOLUCION La primera canica extraída (sujeto activo) puede ser cualquiera de las 4 (opciones). La segunda canica puede ser cualquiera de las tres (opciones) restantes. Esto puede representar gráficamente de la siguiente manera: Primera canica Segunda canica Orden Azul Negra Roja Verde AN AR AV Negra Azul Roja Verde NA NR NV Roja Azul Negra Verde RA RN RV Verde Azul Negra Roja VA VN VR 2 Si se aplica la fórmula para calcular las permutaciones: ______________________ Permutaciones de n objetos tomados de r en r ______________________ = nPr n! _______________________ = (n - r ) 4! ________________ = (4–2) ! Permutaciones = 24 _________ 2 = ! 12 EJERCICIO: La mesa directiva (presidente, secretario y tesorero) de una asociación va elegirse de entre cinco candidatos, identificados con las letras A, B, C, D y E. Suponga que cualquiera de ellos se apto para cualquier puesto y determine el número de formas diferentes ñeque puede quedar integrada la mesa directiva. SOLUCIÓN: El primer puesto puede ser ocupado por cualquiera de las cinco personas; el segundo puesto puede ser ocupado por cualquiera de las tres personas restantes, por lo que el número de formas diferentes será: Permutaciones = 5 * 4 * 3 = 60 Este resultado puede obtenerse por medio de la fórmula de las permutaciones, como se presenta a continuación: ______________________ Permutaciones de n objetos tomados de r en r ______________________ = nPr n! = ______________ (n - r ) ! 5! = ___________ = 60 (5 - 3) ! Observe que la mesa directiva formada por las personas A, B, y C es diferente de la mesa integrada por las personas A, C y B; B, A y C; B, C y A; C, A y B; o C, B, y A. Verifique el cálculo de las siguientes permutaciones: 6P4 = 25P11 20 000P 100 = = 360 1.7792 E14 9.8931 E429 PERMUTAR TODOS LOS OBJETOS, DE TODOS DIFERENTES El número de formas diferentes en que pueden ordenarse n objetos diferentes cuando se toman de uno en uno es el factorial de n (n !), tal como se representa a continuación. Observe que n ! crece rápidamente, por ejemplo, si n es igual a 15, su factorial es 1 307 674 368 000. EJERCICIO: En una caja hay cuatro canicas (azul, negra, roja y verde) Si se extraen una por una de la caja ¿en qué orden pueden aparecer? SOLUCION El primer puesto puede ser ocupado por cualquiera de las cinco personas; el segundo puesto puede ser ocupado por cualquiera de las cuatro personas restantes, y el tercer puesto puede ser ocupado por cualquiera de las tres personas restantes, por lo que el numero de formas diferentes será: 3 Si aplica la formula correspondiente a este caso, el numero de formas será: n = 4! = 4 * 3 *2 = 24. EJERCICIO: En una caja hay un billete de Q.100.00, otro de Q.10.00 y uno de Q.1.00. Tres personas van a tomar cada una un billete, sin ver. Determine las formas en que pueden distribuirse los billetes. SOLUCIÓN: La primer persona (sujeto activo) puede tomar cualquiera de los tres billetes (opciones); la segunda persona (sujeto activo), uno dedos billetes restantes (opciones), y la ultima persona, el billete que quede en la caja. Esto equivale a tener (3 * 2 * 1 = 3 ! = 6) formas diferentes. Primera Persona Q.100.00 Persona Segunda Q.10.00 Q. 1.00 Tercera Persona Q.1.00 Q.10.00 Forma Distribución 1 2 Q.100.00 Q.100.00 Q.10.00 Q.1.00 Q.1.00 Q. 10.00 Q. 10.00 Q. 100.00 Q.1.00 Q.1.00 Q.100.00 3 4 Q.10.00 Q.10.00 Q.100.00 Q.1.00 Q.1.00 Q.100.00 Q.1.00 Q.100.00 Q.10.00 Q.10.00 Q.100.00 5 6 Q.1.00 Q.1.00 Q.100.00 Q.10.00 Q.10.00 Q.100.00 PERMUTAR TODOS LOS OBJETOS, DE ALGUNOS REPETIDOS El numero de formas diferentes en que pueden ordenarse K1, K2,…, y Kn objetos iguales entre si, cuando se toman de uno por uno, es el factorial de (K1, + K2, + … + Kn), entre el producto de los factoriales de K1, K2,…, y Kn. Es decir, (K1 + K2 +…+ Kn)! Formas = ________________ (K1! * K2! *…* Kn)! EJERCICIO En una caja hay dos canicas verdes. Si se extraen una por una de la caja, ¿en qué orden pueden aparecer? 4 SOLUCION La primera canica extraída puede ser roja o verde; la segunda también, pero la tercer solo puede ser verde si las dos primeras fueron rojas. Las formas en las que pueden aparecer estas canicas se presentan a continuación: (K1 + K2 +…+ Kn)! Formas = ________________ (K1! * K2! *…* Kn)! (2 + 5) ! Formas = ________ 2! * 5! 5040 = _______ 2* 120 = 21 PERMUTAR ALGUNOS OBJETOS, DE ALGUNOS REPETIDOS No existe una fórmula fácil para determinar el numero de permutaciones cuando se toman algunos objetos de un conjunto que contiene varios artículos iguales entre si. El ejemplo que aquí se presenta se resuelve por medio de un diagrama. EJERCICIO En una caja hay 2 canicas rojas y 5 verdes. Si se extraen cuatro de ellas de la caja, ¿en qué orden aparecen? SOLUCION La primera canica extraída (sujeto activo) puede ser roja o verde (opciones);la segunda también pero a la tercera y cuarta canicas solo les queda ser verde si dos de las canicas anteriores fueron rojas. Las formas en las que pueden aparecer estas canicas se presentan a continuación: 5 PERMUTACIONES CON REEMPLAZO En todos los ejemplos anteriores, el numero de objetos estaba perfectamente definido (4 canicas, 3 billetes, etc.). sin embargo, es frecuente que el número de objetos sea limitado, pero que el numero de veces que se presenten sea infinito, por ejemplo, cuando los objetos seleccionados pueden ser elegidos de nuevo. La diferencia entre una situación y otra se conoce como reemplazo y se siguiente ejemplo: EJERCICIO presenta en el - Los resultados posibles de un juego son perder o ganar. Si se juegan cuatro juegos, ¿cuáles son los resultados posibles? SOLUCION Cada uno de los cuatro juegos (sujeto activo) puede terminar en cualquiera de los resultados posibles (opciones). Esto se muestra gráficamente a continuación: El número de formas diferentes en que puede aparecer n objetos diferentes, en m intentos, con reemplazo, es; (n ** m). En este caso, 2 ** 4 = 16 formas diferentes. Compruebe que si n = 3 y m = 5, el numero de formas diferentes será 243; y que si n = 5 y m = 3, el numero de formas diferentes será 125. COMBINACIONES Una combinación es una forma en la que pueden presentarse los objetos o eventos, y en la que el orden de aparición no importa; por ejemplo; la multiplicación de los dígitos, 2, 5 y 8 puede hacerse de muchas formas diferentes, por ejemplo, 2 * 5 * o 2 * 8 * 5, pero en todos los casos el resultado será el mismo. Los factores 2, 5, y 8; 2, 8, y 5, etc., son combinaciones de los dígitos 2, 5 y 8. La fórmula general de las combinaciones d! es la siguiente: ___________________ Combinaciones n objetos = tomados de en r ___________________ n nCr = r = _n !____ r! * (n-r)! 6 n es el numero total de objetos o eventos. r es el numero de objetos que se desea considerar (n puede ser cualquier valor entero positivo; puede ser cualquier valor entero positivo desde 1 hasta n ) Observe que, para cualquier pareja de números enteros positivos n y r, exceptuando r = 1, el numero de permutaciones es mayor que el de combinaciones. Por ejemplo, si n = 7 y r = 4, 7P4 = 840 Y 7c4 = 35. EJERCICIO En un grupo hay 5 personas, las que pueden identificarse con las letras A, B, C, D y E. De ellas se van a seleccionar 3 para una misión especial. ¿de cuántas formas diferentes se pueden seleccionar las 3 personas? SOLUCION Observe que la misión formada por las personas A, B, C y D se considera igual a la misión integrada por las personas B,C y A (o CAB, CBA, etc.) por lo que en este caso puede aplicarse la formula para calcular el numero de las combinaciones posibles de un total de 5 elementos, tomados de 3 en 3, el cual está dado por: Combinaciones de n objetos tomados de r en r 5 5C3 = 3 n = nCr = r n! = ___________ r ! * (n– r ) ! 5! =_____________ = 10 3! *(5 – 3) ! La misión especial puede quedar integrada por las personas: ABC, ABD, ABE, ACD, ACE, ADE, BCD, BCE, BDE, Y CDE, es decir, 10 formas diferentes. EJERCICIO: En una bolsa hay 6 monedas, marcadas con los números 1, 2, 3, 4, 5, y 6. Se van a tomar al azar 4 monedas. ¿De cuántas formas diferentes se pueden tomar las monedas? SOLUCION Observe que el grupo formado por las monedas 1, 2, 3, y 4 se considera igual al grupo formado por las monedas 1, 2, 4 y 3 ( o 1423, 1432, 4123, 4132, etc.), por lo que en este caso puede aplicarse la fórmula para calcular el número de las combinaciones posibles de un total de 6 elementos, tomados de 4 en 4, el cual está dado por: Combinaciones de n objetos tomados de r en r 6 6C4 = 4 n = nCr = r n! = ___________ r ! * (n– r ) ! 6! =_____________ = 15 4! *(6 – 4) ! Las monedas seleccionadas podrían ser las siguientes: 1234, 1235, 1236, 1245, 1256, 1246, 1256, 1345, 1346, 1356, 1456, 2345, 2346, 2356, 2456 y 3456, esto es, 15 formas diferentes. SCLS/mirna 31/03/2016 09:31 horas