Gu a para resoluci n de problemas An lisis combinatorio
Anuncio

Guía para identificar problemas de análisis combinatorio.
Ordenaciones (permutaciones) con reemplazo (repetición)
- El orden es importante
- Los elementos se pueden usar más de una vez.
n
Rr n r
Ordenaciones (permutaciones) sin reemplazo (repetición)
- El orden es importante
- Los elementos solo se pueden utilizar una vez.
n
n!
n r!
Pr
En ambos casos la n es el conjunto del cual vas a sacar elementos para permutar,
y la r el número de elementos que vas a sacar de ese conjunto original y que vas a
ordenar (permutar).
Combinaciones
- Se buscan el número de subconjuntos distintos de tamaño r que se pueden
crear a partir de un conjunto original n
- El orden dentro de los subconjuntos no importa. Ej. {1,2} = {2,1}
- Aquí, la n es el conjunto original y la r es el número de elementos que van en
cada uno de los subconjuntos.
n
Cr
n!
r!n r!
Permutaciones con objetos indistinguibles
-
El orden es importante, pero
Hay elementos en el conjunto original que son idénticos y que se pueden
sustituir uno por el otro. (“para el caso es lo mismo”)
Lo que se busca es el numero de combinaciones distinguibles.
Pnn 1 ,n 2 ,...,n k
n!
n1!n2 !... n k!
Para las permutaciones con objetos indistinguibles, las ni son el numero de objetos
idénticos de cada tipo. Ej. Para la palabra “atotonilco”, existen dos “o” y dos “t”, por lo
tanto n = 10, no = 2 y nt = 2.
1
Esta fórmula se emplea también cuando se quieren obtener subconjuntos de
diferentes tamaño, ni de un conjunto n, es decir particiones del conjunto. Por ejemplo:
¿De cuantas formas es posible dividir un conjunto de cinco objetos en tres subconjuntos
que contengan respectivamente, 2, 2 y 1 de los objetos? Si estos objetos fuesen las
vocales, entonces n = 5 ({a, e, i, o, u} ), n1 = 2, (un subconjunto de tamaño 2) n2 = 2 (otro
subconjunto de tamaño 2) y n3 = 1 (un subconjunto de tamaño 1).
Como queremos particionar el conjunto original, entonces lo representamos de la
siguiente forma:
n
n!
n ,n ,...,n
n !n !... n !
1 2
k
1
2
k
Permutaciones cíclicas o circulares usando todos los elementos.
n
Se utiliza cuando queremos ordenar objetos en círculo. (personas en una mesa,
redonda, llaves en un llavero de argolla, etc.
el orden es importante pero
el orden de los elementos es sólo relativo al resto de los elementos ordenados.
PCr (n 1)!
- Cuando existen restricciones de personas u objetos que se tienen que sentar o estar
juntas se convierte en un problema de permutación sin reemplazo
2
3
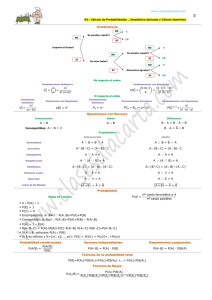
Aná li sis Comb in atorio.
Per mutación c íc li ca
Sí
Sí
¿Se r equ ie re or gan iz ar a
todos los e le mentos al
re dedo r de un c ír culo?
Sí
No
¿Es impo rtante el or den
de los eleme ntos?
Per mutación
con r eemp la zo
¿Ex is te n elementos
indistinguibles ?
Sí
No
No
¿Lo s subc onjuntos
son d el mismo
tamaño ?
Sí
Par tic ió n
4
¿Se p uede n usar lo s
elemen to s del conjun to
or ig in al má s de una v ez?
No
Combina ción
No
Per mutación c on
elemen to s in distin guibles.
Per mutación
sin re emplazo