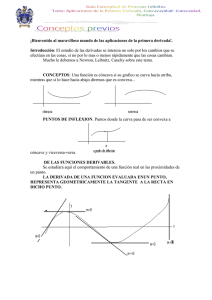
Gráficas. E: Sea la función f(x) = x x2 + 1 . Diga en qué intervalos es
Anuncio

16 Gráficas. E: Sea la función f (x) = x2 x . +1 Diga en qué intervalos es cóncava hacia arriba, cóncava hacia abajo, determine los puntos de inflexión y grafique. D: H Calculemos primero la primera y la segunda derivada x2 + 1 − 2x2 1 − x2 = ⇒ (x2 + 1)2 (x2 + 1)2 −2x(x2 + 1)2 − 2(x2 + 1)2x(1 − x2) −2x(x2 + 1) − 4x(1 − x2) = = f 00 (x) = (x2 + 1)4 (x2 + 1)3 −2x3 − 2x − 4x + 4x3 2x3 − 6x = = . (x2 + 1)3 (x2 + 1)3 f 0 (x) = Luego, los puntos de inflexión se encuentran cuando √ 2x3 − 6x = 2x(x2 − 3) = 0 ⇔ x = 0 & x = ± 3 . El signo de la segunda derivada nos lo da esta misma expresión, pues el denominador (x2 + 1)3 siempre es positivo. Determinemos el signo de la segunda derivada: Intervalo √ √ x < − 3(< 0 < 3) √ √ − 3 < x < 0(< 3) √ √ (− 3 <)0 < x < 3 √ √ (− 3 < 0 <) 3 < x Signo de √ √ x + 3 x x − 3 f 00(x) f (x) es cóncava hacia − − − − abajo + − − + arriba + + − − abajo + + + + arriba √ √ √ √ Habida cuenta que 2x(x2 − 3) = 2x(x + 3)(x − 3) y su signo nos lo da x(x + 3)(x − 3). Además: Df = R ; la única raı́z de f es x = 0 & f es impar. 1 x lı́m f (x) = lı́m = 0, por lo que y = 0 es ası́ntota horizontal. 1 x→±∞ x→±∞ 1+ 2 x Los puntos crı́ticos de f son x = ±1 cuando f 0 (x) = 0. 16 canek.azc.uam.mx 1 2 El signo de f 0 (x) nos lo da 1 − x2 = (1 + x)(1 − x), luego: Signo de Intervalo 1 + x 1 − x f 0(x) f (x) es x < −1(< 1) − + − decreciente −1 < x < 1 + + + creciente (−1 <)1 < x + − − decreciente 1 hay un máximo relativo pues f pasa de ser creciente a ser decreciente. 2 1 En x = −1, f (−1) = − hay un mı́nimo relativo pues f pasa de ser decreciente a ser creciente. 2 √ √ ± 3 f (± 3) = ≈ ±0.4330127 ası́ como f (0) = 0 son las ordenadas de los puntos de inflexión. 4 Y con toda esta información la gráfica de f es: f (x) En x = 1, f (1) = 1 2 0.433 √ − 3−1 1 x √ 3 −0.433 − 12