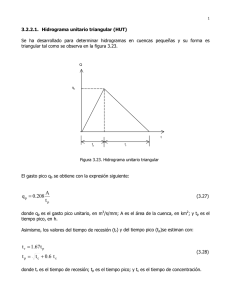
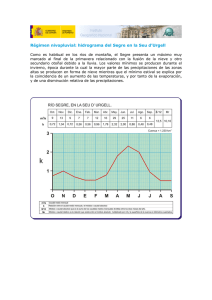
Hidrograma Unitario

Hidrograma Unitario
Por Laura Ibáñez Castillo
1
Hidrograma
• Un hidrograma es una gráfica continua tiempo contra gasto
(volumen / unidad de tiempo) producido por una lluvia de
cualquier magnitud para una duración específica. Un
hidrograma puede ser el resultado de un proceso de aforos
en un río.
Gasto en ft3/sec
HIDROGRAMA DE TORMENTA
20000
15000
10000
5000
0
0
2
4
6
8
10 12 14 16 18
Tiempo en horas
2
¿Como predecir un hidrograma
para una tormenta ocurriendo
en tiempo real (pronóstico) o el
hidrograma para una tormenta
diseño en una cuenca
(planeación)?
HIDROGRAMA UNITARIO
3
Hidrograma en tiempo real
igual a
Lluvia Efectiva en tiempo real *Hidrograma Unitario
+
Flujo Base
4
Componentes de un
hidrograma
• Flujo superficial ó Escurrimiento
directo (pudiendo incluir interflujo)
• Flujo Base o Flujo subterráneo
somero
Esc. directo
Flujo base
5
¿De que es resultado el
hidrograma?
El hidrograma es la “huella digital”
de la cuenca y “captura” la relación
lluvia-escurrimiento en una cuenca
y es el resultado de:
• Condiciones meteorológicas
• Condiciones fisiográficas, y,
• Condiciones de usos del suelo
6
Factores Climáticos que
Influyen en el hidrograma
• Intensidad de la lluvia
• Duración de la lluvia
• Distribución espacial de la lluvia
sobre la cuenca
7
Factores Fisiográficos que
Influyen en el hidrograma
•
•
•
•
Tamaño y forma del área drenada
Distribución de la red de corrientes
Pendientes de laderas y cauces
Almacenamientos
naturales
o
artificiales
que
amortiguan
avenidas
8
La influencia del Uso del Suelo en
el hidrograma
• La presencia o ausencia de cubierta
vegetal (urbanización) reduce o
incrementa las velocidades con que
se mueve el agua en la cuenca
influenciando el gasto pico.
• La cubierta vegetal incrementa la
cantidad de agua infiltrada en el
suelo
• La vegetación intercepta lluvia
9
Proceso LluviaLluvia-Escurrimiento
10
Esquema del proceso LluviaLluviaEscurrimiento
L lu v ia
I n t e r c e p c ió n p o r v e g e t a c ió n
E v a p o r a c ió n y E V T *
A l m a c e n a m ie n t o e n p e q u e ñ a s d e p r e s io n e s
A l m a c e n a m ie n t o a m o r t ig u a d o r
I n f i lt r a c ió n
F lu jo
S u p e r f ic ia l
A g u a S u b t e rrá n e a
F lu jo S u p e r f ic ia l
D i re c t o
F lu jo B a s e
D i re c t o
I n t e r f lu jo
Q e n h id r o g r a m a s
e s c u r r i m ie n t o e n
c o r r ie n t e s
o
* P a r a u n a to r m e n ta d e d u r a c ió n m e n o r a 2 4
h o r a s (d ía
n u b la d o ) l a E V T p u e d e
ser
d e s p r e c ia b l e .
R e p r e s e n ta
por
m u c ho
a p r o x im a d a m e n te 2 % . S i lo q u e s e h a c e e s
u n b a l a n c e h id r o ló g i c o s e m a n a l, m e n s u a l
y / o a n u a l s í d e b e s e r c o n s id e r a d a .
11
LLEGANDO AL CONCEPTO DE
HIDROGRAMA UNITARIO…
NO PERDER DE VISTA EL CONCEPTO
DE ESCURRIMIENTO DIRECTO O
LLUVIA EXCESO
12
Lluvia Exceso o Escurrimiento
Directo o Lluvia efectiva
• Lluvia Bruta = Almacenamiento en
depresiones + evaporación + infiltración +
escurrimiento superficial
• Lluvia Exceso = Lluvia Bruta – (infiltración
+Almacenamiento en depresiones), ó,
• Lluvia Exceso = Lluvia Bruta – pérdidas
* Almacenamiento amortiguador puede ser incluído en
escurrimiento superficial; EV y EVT despreciadas.
13
Lluvia Exceso o Escurrimiento
Directo
Lluvia Exceso o Escurrimiento Directo o
Lluvia Efectiva = Lluvia Bruta – infiltració*
*Finalmente el contingente más grande de las pérdidas será
formado por la infiltración.
14
Hidrograma Unitario
(Sherman, 1932; Horton, 1933)
• El hidrograma que resulta de 1-mm de lluvia exceso (o 1 pulgada o 1
cm) distribuido uniformemente en espacio sobre un área para una
duración dada.
• Los puntos clave:
1-mm de lluvia EXCESO
La lluvia exceso está distribuída uniformemente en espacio
sobre un área
La lluvia exceso tiene una duración asociada
15
Supuestos del Hidrograma
Unitario (Aparicio, p. 209)
Excesos de Lluvia de igual duración producen hidrogramas con
tiempos bases equivalentes sin importar la intensidad de la
lluvia
Las ordenadas del escurrimiento directo para una tormenta de
una duración dada se suponen directamente proporcionales
(lineales) a los volúmenes de exceso de lluvia. Por lo tanto el
doble de exceso de lluvia produce el doble de las ordenadas del
hidrograma.
Superposición de causas y efectos. El hidrograma que resulte de
un periodo de lluvias puede superponerse a hidrogramas
resultantes de lluvias previas o posteriores.
16
Representación Gráfica
tiempo al pico y tiempo base
Duración de la
lluvia exceso
Tiempo al
pico
Tiempo Base
Flujo base
17
Métodos para determinar el
Hidrograma Unitario
• Tradicional: A partir de datos de
precipitación y aforos
• Sintéticos
– Soil Conservation Service (SCS) ó
método del número de curva
– Snyder
– Time-Area (Clark, 1945)
18
Método Tradicional
1) Separar flujo base de flujo directo
2) Cálculo del volumen de escurrimiento directo. Medir el volumen
total bajo el hidrograma
3) Cálculo de la altura de precipitación efectiva : dividir Vol. Esc.
Directo entre area de la cuenca y obtenerlo en mm o cm o pulgadas
4) Derivar las ordenadas del hidrograma unitario dividiendo las
ordenadas del hidrograma total entre la altura precipitación efectiva
del punto 3
5) Determinar duración efectiva separando lluvia efectiva e infiltración
y viendo la duración de la lluvia efectiva (en este momento hacerlo
con el indice de infiltración media, φ)
19
Indice de Infiltración Media, φ
10
8
Duración lluvia
Exceso= 4
horas
Lluvia exceso=
6 mm
φ= 2.5 mm/hr
6
4
Infiltración=
17 mm
2
0
0-2
2-4
4-6
6-8
8-10
20
EJEMPLO-DETERMINACION H.U.
METODO TRADICIONAL
Determinar H.U. para una cuenca de 888 Km2
Hietograma de altura de precipitacion :
Tiempo (horas)
0-2
2-4
4-6
6-8
8-10
Precipitación, Hp (mm)
7.0
9.0
4.0
1.0
2.0
21
EJEMPLO H.U. METODO TRADICIONAL
Hidrograma de escurrimiento medido a la salida de
la cuenca:
Tiempo (horas)
0
2
4
6
8
10
12
14
Gasto, Q (m3/s)
40.0
80.0
220.0
300.0
200.0
120.0
60.0
40.0
22
Separation of Baseflow
... generally accepted that the inflection point on the recession limb of a
hydrograph is the result of a change in the controlling physical processes
of the excess precipitation flowing to the basin outlet.
In this example, baseflow is considered to be a straight line connecting
that point at which the hydrograph begins to rise rapidly and the
inflection point on the recession side of the hydrograph.
the inflection point may be found by plotting the hydrograph in semilog fashion with flow being plotted on the log scale and noting the time
at which the recession side fits a straight line.
23
Semi--log Plot
Semi
10 0 00 0
Reces sio n sid e o f hydro grap h
be co me s line ar at ap pro xim ately ho ur
6 4.
1 0 00 0
Fl o w (cfs )
1 000
100
10
10
4
10
9
11
4
11
9
12
4
12
9
13
4
94
99
89
79
84
74
69
59
64
54
49
44
39
29
34
1
Tim e (hrs. )
24
Hydrograph & Baseflow
250 00
200 00
Flo w (c fs)
150 00
100 00
50 00
133
126
11 9
112
105
98
91
84
77
70
63
56
49
42
35
28
21
14
7
0
0
T im e (h rs.)
25
Separate Baseflow
25000
20000
Flo w (cfs )
15000
10000
5000
6
9
2
5
3
13
12
11
11
10
98
91
84
77
70
63
56
49
42
35
28
21
7
14
0
0
T im e (hrs.)
26
Sample Calculations
• In the present example (hourly time step), the flows are summed and
then multiplied by 3600 seconds to determine the volume of runoff in
cubic feet. If desired, this value may then be converted to acre-feet by
dividing by 43,560 square feet per acre.
• The depth of direct runoff in feet is found by dividing the total volume
of excess precipitation (now in acre-feet) by the watershed area (450
mi2 converted to 288,000 acres).
• In this example, the volume of excess precipitation or direct runoff for
storm #1 was determined to be 39,692 acre-feet.
• The depth of direct runoff is found to be 0.1378 feet after dividing by
the watershed area of 288,000 acres.
• Finally, the depth of direct runoff in inches is 0.1378 x 12 = 1.65
inches.
27
Obtain UHG Ordinates
• The ordinates of the unit hydrograph are
obtained by dividing each flow in the direct
runoff hydrograph by the depth of excess
precipitation.
• In this example, the units of the unit
hydrograph would be cfs/inch (of excess
precipitation).
28
Final UHG
25 000
St orm # 1 h yd rograp h
St orm #1 dire ct run o ff
h yd rog ra ph
20 000
Flo w (c fs)
15 000
S torm # 1 u nit
hyd rograp h
10 000
S torm # 1
b as eflo w
5 000
1 33
1 26
1 19
11 2
1 05
98
91
84
77
70
63
56
49
42
35
28
21
14
7
0
0
T im e (h rs. )
29
Determine Duration of UHG
• The duration of the derived unit hydrograph is found by examining the
precipitation for the event and determining that precipitation which is
in excess.
• This is generally accomplished by plotting the precipitation in
hyetograph form and drawing a horizontal line such that the
precipitation above this line is equal to the depth of excess
precipitation as previously determined.
• This horizontal line is generally referred to as the Φ-index and is based
on the assumption of a constant or uniform infiltration rate.
• The uniform infiltration necessary to cause 1.65 inches of excess
precipitation was determined to be approximately 0.2 inches per hour.
30
Estimating Excess Precip.
0.8
0.7
Precipitation (inches)
0.6
0.5
Uniform loss rate of
0.2 inches per hour.
0.4
0.3
0.2
0.1
0
0
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19
Time (hrs.)
31
Excess Precipitation
1
0.9
De rived unit hydrog rap h is the
result of ap pro xim ately 6 hours
of exce ss p re cip ita tio n.
0.8
Exc ess P rec. (in ch es)
0.7
0.6
0.5
Sma ll a mo unts o f
exce ss pre cipita tio n a t
be ginning and e nd ma y
b e o mitted .
0.4
0.3
0.2
0.1
0
0
1
2
3
4
5
6
7
8
9
10 11 1 2
13 14 1 5
16
17 1 8
19
T im e (h rs.)
32
Cambiando la Duración
• Muy frecuentemente será neceario cambiar la duración del
hidrograma unitario de duración de lluvia efectiva de a de´
• El método de alterar la duración de un hidrograma unitario
es el método de la curva S.
• Se basa en el principio de superposición de causas y
efectos, es decir, parte del hecho de que una secuencia de
lluvias produce un hidrograma igual a la suma de los
hidrogramas que produciría cada lluvia en particular
• El método consiste en desplazar un hidrograma unitario su
duración y sumar las ordenadas.
33
Método de la Curva S
1. Se desplaza varias veces el hidrograma unitario conocido,
de tal manera que la separación entre cada hidrograma sea
igual a la duración de.
2. Se suman las ordenadas de los hidrogramas unitarios
desplazados, con lo que se obtiene un hidrograma llamado
la curva-S que corresponde a la lluvia efectiva con
intensidad constante i = 1 mm/ de, mantenida durante un
tiempo muy grande y que eventualmente (en tc) llevará a la
cuenca a un escurrimiento equilibrio (todo lo que precipita,
escurre):
1mm
Qe = i × Ac =
× Ac
de
34
... Continúa Curva S
3. Se desplaza la curva S una distancia igual a de´.
4. Se restan las ordenadas obtenidas en (3) de la curva S
5. Las ordenadas del hidrograma unitario deseado (duración
de´) se obtienen multiplicando los resultados obtenidos en
el paso 4 por el cociente de/de´
35
EJEMPLO
H.U. (P.ef.=1 mm), de = 4 hs., Ac=888 Km2
Cambiar a H.U. de´=2 hrs.
Tiempo (horas)
0
2
4
6
8
10
12
14
Gasto, Q (m3/s)
0.0
6.67
30.0
43.33
26.67
43.33
3.33
0
36
T (hs) H.U. Despl. Despl. Despl. Despl. Curva Curva
De=4
S
S
0
0
0
0
2
6.67
4
30.0
6
43.33 6.67
8
26.67 30.0
10
13.33 43.33 6.67
12
3.33
26.67 30.0
14
0
13.33 43.33 6.67
0
0
6.67
6.67
30.0
30.0
50.0
50.0
56.67 56.67
63.33 61.67
0
60.0
61.67
63.33 61.67
16
3.33
26.67 30.0
0
18
0
13.33 43.33 6.67
60.0
61.67
63.33 61.67
37
*Corrección a Gasto equilibrio
1 mm
Qe = i × A =
Ac
de
A
888
Qe =
=
= 61.67
3.6 × de 3.6 × 4
38
Curva S para d.e. = 4 hs
H.U. = 1 mm
Método de la Curva S
G a sto (m 3/s)
80
60
H.U.- 4hs.
40
Curva-S
20
0
0 2 4 6 8 10 12 14 16 18
horas
39
CURVA-S
• La diferencia de las curva S y la curva-S desplazada de´ es
el hidrograma resultante de una lluvia con intensidad
constante 1mm/de que cae durante de´ horas. Para que el
hidrograma unitario resultante sea unitario, la intensidad de
la precipitación debe ser 1/de´, entonces es necesario
multiplicar sus ordenadas por de/de´:
1 de
1
=
de de´ de´
40
De/de´
de = 4 hs.; de´= 2 hs.
de 4
= = 2.0 (multiplicar por esto)
de´ 2
41
Curva S
(4 horas)
S despl. 2
hs.
0
Diferencia
0
H.U. - 2hs.
(m3/s)
Dif. x de/de’
0
6.67
0
6.67
13.33
30.0
6.67
23.33
46.67
50.0
30.0
20.0
40.0
56.67
50.0
6.67
13.33
61.67
56.67
5.0
10.0
61.67
61.67
0.0
0
61.67
61.67
42
61.67
61.67
de/de´=2.0
H.U. = 1 mm
d.e.´´ = 4 hs
d.e.
Gasto en m3/s
H.U. para de´=2 horas
60
40
20
0
0
2
4
6
8
10
12
tiempo en horas
43
Hidrogramas Unitarios
Sintéticos
•
•
•
•
Chow
SCS (triangular y curvilíneo)
Snyder
Clark
44
Hidrogramas Unitarios
Sintéticos
• Para cuencas no aforadas
• Se usan las características generales de las
cuencas (p. ej. tiempo de concentración),
por lo que se utilizan formulas empíricas
• Son para duraciones efectivas críticas
45
H.U. Sintético Triangular del SCS
Duration of
excess
precipitation.
Tiempo de retraso, tr
Tiempo al pico, tp
Tiempo base, tb
46
H.U. SCS gasto pico
A Partir de la geometría de la figura y con la debida
conversión de unidades:
0.555 Ac
qp =
,
tb
(1)
A = area de la cuenca en km2
t b = tiempo base en horas
q p = gasto pico unitario en m3/s/mm
47
Deducción de la ecuación de qp
q
T ×
Vol .
2
1 mm =
=
A
A
b
c
c
T ×q
1 mm =
,
2A
b
despejando q
c
2 A × 1 mm
q=
,
T
c
b
Para tener las unidades necesarias :
q en m3/s, A en Km2 y Tb en horas :
0.2777 × 2 × A
0 . 555 × A
q=
=
T
T
c
b
b
c
48
H.U. SCS tiempos
•
•
•
•
•
TIEMPO BASE, tb
TIEMPO AL PICO, tp
TIEMPO DE RETRASO Ó LAG-TIME, tr
DURACIÓN EFECTIVA DE LA LLUVIA, de
TIEMPO DE CONCENTRACIÓN, tc
49
H.U. SCS tiempos
De acuerdo a Mockus (analisis de hidrograma s) :
t b = 2 . 67 × t p
(2)
De acuerdo a la figura :
de
tp =
+ tr
2
De acuerdo a Mockus :
t r = 0 .6 × t c
(4)
d e = 0 . 1333 × t c
(5 )
(3)
50
H.U Triangular Del SCS
Por lo tanto sustituyendo (4) y (5) en (3) :
2
t p = tc
(6)
3
Una vez estimado t p , q p puede ser reformulado como :
0.208 × Ac
qp =
tp
(7 )
Y la formula empírica de tiempo de concentración (hs), SCS :
0.7
 1000 
0.00227 × L 
− 9
CN


tc =
(8)
0.5
Y
L = Longitud del cauce ppal. en m (longest flow path)
51
Y = pendiente promedio de cuenca en %; CN = numero curva
0.8
H.U. Sintético Curvilíneo del SCS
Se requiere qp y tp:
2
t p = tc
3
0 . 208 × Ac
qp =
tp
(6)
(7 )
 1000

0 . 00227 × L 
− 9
CN


tc =
Y 0 .5
0 .7
0 .8
(8 )
52
H.U. Sintético Curvilíneo del SCS
• Se debe tener calculado el tp y qp
• Para encontrar abscisas del hidrograma se
multiplica el “time ratio” por el tiempo al pico (tp)
• Para encontrar las ordenadas del hidrograma se
multiplica el “Discharge ratio” por el gasto pico
(qp)
53
SCS
SCS Dimensionless UHG Features
1
Flow ratios
Cum. Mass
0.8
Q/Qpeak
0.6
0.4
0.2
0
0
0.5
1
1.5
2
2.5
T/Tpeak
3
3.5
4
4.5
5
54
Dimensionless Ratios
Time Ratios
(t/tp)
0
.1
.2
.3
.4
.5
.6
.7
.8
.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
2.2
2.4
2.6
2.8
3.0
3.2
3.4
3.6
3.8
4.0
4.5
5.0
Discharge Ratios
(q/qp)
.000
.030
.100
.190
.310
.470
.660
.820
.930
.990
1.000
.990
.930
.860
.780
.680
.560
.460
.390
.330
.280
.207
.147
.107
.077
.055
.040
.029
.021
.015
.011
.005
.000
Mass Curve Ratios
(Qa/Q)
.000
.001
.006
.012
.035
.065
.107
.163
.228
.300
.375
.450
.522
.589
.650
.700
.751
.790
.822
.849
.871
.908
.934
.953
.967
.977
.984
.989
.993
.995
.997
.999
1.000
55
Triangular Representation
D
SCS Dimensionless UHG & Triangular Representation
Excess
Precipitation
1.2
Tlag
1
0.8
Flow ratios
Q/Qpeak
Cum. Mass
Triangular
0.6
Point of
Inflection
Tc
0.4
0.2
0
0.0
Tp
1.0
2.0
Tb
3.0
4.0
5.0
T/Tpeak
56
Triangular Representation
T b = 2.67 x T p
D
SCS Dimensionless UHG & Triangular Representation
Excess
Precipitation
1.2
Tlag
1
Tr = Tb - Tp = 1.67 x Tp
0.8
Flow ratios
Q/Qpeak
Cum. Mass
Triangular
0.6
Point of
Inflection
Tc
Q=
qpT p
2
+
qpT r
2
=
qp
2
0.4
(T p +T r )
0.2
0
0.0
qp =
qp=
2Q
T p +T r
654.33 x 2 x A x Q
T p +T r
qp =
484 A Q
Tp
Tp
1.0
2.0
Tb
3.0
4.0
5.0
T/Tpeak
The 645.33 is the conversion used for
delivering 1-inch of runoff (the area
under the unit hydrograph) from 1-square
mile in 1-hour (3600 seconds).
57
484 ?
qp =
484 A Q
Tp
Comes from the initial assumption that 3/8 of the volume
under the UHG is under the rising limb and the remaining 5/8
is under the recession limb.
General Description
Peaking Factor
Urban areas; steep slopes
Typical SCS
Mixed urban/rural
Rural, rolling hills
Rural, slight slopes
Rural, very flat
575
484
400
300
200
100
Limb Ratio
(Recession to Rising)
1.25
1.67
2.25
3.33
5.5
12.0
58
Duration & Timing?
Again from the triangle
T p=
D
+L
2
L = Lag time
L = 0.6 * Tc
Tc + D = 1.7 T p
D
+ 0.6 T c = T p
2
For estimation purposes :
D = 0.133 Tc
59
A Regression Equation
L0.8 (S + 1) 0.7
Tlag =
1900(% Slope) 0.5
where : Tlag = lag time in hours
L = Length of the longest drainage path in feet
S = (1000/CN) - 10 (CN=curve number)
%Slope = The average watershed slope in %
60
Snyder
• En 1938 Snyder estudio varias cuencas en las montañas Apalaches
(varios estados del Este de los E.U.A.)
• Las cuencas variaban de 10 mi2 a 10,000 mi2 (30 a 30,000 Km2)
• Encontró relaciones entre características de las cuencas y su
hidrograma unitario
• En 1959, el U.S. Army Corps of Engineers confirmó dichas relaciones
• Concluyeron que las relaciones obtenidas en las cuencas
instrumentadas (pluviografos y aforos), pudieran ser extrapolados a
cuencas no instrumentadas para deducir su hidrograma unitario
basados en parámetros de la cuenca instrumentada
• La cuenca instrumentada y la no instrumentada deben estar en la
misma región y con características semejantes
61
Hidrograma unitario sintético Snyder:
las cinco características necesarias
Para una lluvía de duración efectiva o duración exceso de
• El gasto pico, qp
• El tiempo de retraso o lag time, tr
• El tiempo base, tb
• Ancho del hidrograma unitario en unidades de tiempo al
50% del gasto pico, W50
• Ancho del hidrograma unitario en unidades de tiempo al
75% del gasto pico, W75 .(El ancho de W50 y W75 están
ubicados 1/3 antes y 2/3 después del qp)
62
H.U. Snyder
Duration of excess
precipitation, de
Tiempo de retraso, tr
W-75
W-50
Tiempo base, tb
63
Relaciones SnyderSnyder- Sist.Inglés
tr = tiempo de retraso
tr = Ct (L • Lca )0.3
de = duración de la lluvia exceso
L=Longitud del cauce principal, mi
La= Longitud sobre cauce principal desde el
d e = tr
5 .5
punto de salida al centroide de la cuenca, mi
Ct= coeficiente derivado de cuencas
instrumentadas en la misma región
A = Area de la cuenca en mi2
Cp = Coeficiente derivado de cuencas
instrumentadas en la misma región
tb= tiempo base en horas
qp = gasto pico en cfs
tr
tb = 3 +
8
qp =
′
640 AC
tr
p
tr = tr +0.25(d −de )
'
e
64
Relaciones SnyderSnyder- Sist.Inglés

W 75 = 440 

W 50
qp
A



 qp 

= 770 
 A 
− 1 . 08
− 1 . 08
W75 =El ancho del hidrograma unitario en
0.75 el qp, en horas.
W50 =El ancho del hidrograma unitario en
0.50 el qp, en horas.
W-75
W-50
Ambos W’s estan distribuídos 1/3 tiempo
antes del qp y 2/3 del tiempo después de qp
65
Snyder-- Sist.Métrico
Snyder
tr = tiempo de retraso
tr = 0.75• Ct (L • Lca )0.3
de = duración de la lluvia exceso
L=Longitud del cauce principal, km
La= Longitud sobre cauce principal desde el
d e = tr
5 .5
punto de salida al centroide de la cuenca, km
Ct= coeficiente derivado de cuencas
instrumentadas en la misma región
A = Area de la cuenca en km2
Cp = Coeficiente derivado de cuencas
instrumentadas en la misma región
tr
tb = 3 +
8
qp
tb= tiempo base en horas
qp = gasto pico en m3/s
′
2 . 75 AC
=
tr
p
tr = tr +0.25(d −de )
'
e
66
H.U. SnyderSnyder- Sist.Métrico

W 75 = 1 . 22 

W 50
qp
A



 qp 

= 2 . 14 
 A 
− 1 . 08
− 1 . 08
W75 =El ancho del hidrograma unitario en
0.75 el qp, en horas.
W50 =El ancho del hidrograma unitario en
0.50 el qp, en horas.
W-75
W-50
Ambos W’s estan distribuídos 1/3 tiempo
antes del qp y 2/3 del tiempo después de qp
67
Snyder-- Sist.Métrico (Chow, 1988)
Snyder
H.U. ESTANDAR qp
PARA duración de
d e = tr
′
tr = tr +0.25(d 'e−de )
5 .5
tr = 0.75• Ct (L • Lca )
qp
H.U. REQUERIDO qpr
PARA duración de´
2 . 75 AC
=
tr
p
Longitudes en kilometros
Areas en Km2
Gastos en m3/s
Tiempos en horas
0.3
q pR
q ptr
=
t r'
tb =
5 . 56
q PR

W 75 = 1 . 22 

q pR
A



q 
W 50 = 2 . 14  pR 
 A 
− 1 . 08
− 1 . 08
68
H.U. DE CLARKCLARK-BASES
La lluvia exceso es transformada a escurrimiento
directo a través de dos procesos:
•Translado o movimiento del exceso de lluvia desde su
orígen hasta la salida de la cuenca (Relaciones tiempotiempoarea y tiempo de concentración)
•Atenuación o reducción de la magnitud del
escurrimiento a medida que parte del exceso transita
por la cuenca y parte es almacenado en la cuenca
(Coeficiente de almacenamiento, R)
69
H.U. DE CLARK
Clark desarrolló el método en 1943 y en su
planteamiento original era para cuencas
instrumentadas y en los 80’s la U.S. Army Corps of
Engineers lo llevarón a método sintético para
generar H.U.
Parámetros necesarios
•Tiempo de concentración en horas, Tc
•Coeficiente de almacenamiento en horas, R
•Relación de tiempo versus area
70
H.U. de Clark o de AreaArea-Tiempo
71
Incrementos de Area
40
Incremental Area (sqaure miles)
35
30
25
20
15
10
8
5
7
0
1
7
2
3
4
5
6
7
8
Time Increment (hrs)
7
6
6
6
5
2
4
0
3
1
5
72
Curva acumulada de areaareatiempo
9
Cumulative Area (sqaure miles)
8
7
6
5
4
3
2
1
8
0
0
20
40
60
80
100
120
140
160
180
200
7
Time (hrs)
7
7
6
6
6
5
2
4
0
3
1
5
73
Problemas para obtener una
curva de TiempoTiempo-area?
TAi = 1.414Ti1.5
1 − TAi = 1.414(1 − Ti )1.5
for (0 ≤ Ti ≤ 0.5)
for (0.5 ≤ Ti ≤ 1.0)
Ti = Fracción del tiempo de
concentración
Use las curvas sintéticas
area-tiempo de la U.S.
Army Corps of Engineers
(HEC 1990)
TA = Area Acumulada
correspondiente al Ti
74
Como regla general…
R – El coeficiente de almacenamiento lineal
Puede ser estimado apróximadamente 0.75 veces
el tiempo de concentración.
¿SERÁ CIERTO?
75
La cuenca como un tanque de
almacenamiento
76
Tránsito del exceso a través del
“tanque de almacenamiento”
dS
dt
O +O  S − S
I −
=
∆t
 2 
I −0 =
1
2
2
I= flujo de entrada
O = flujo de salida
1
S = Almacenamiento
R = Coeficiente de almacenamiento
(Almacenamiento lineal, S = RO)
 O + O  RO − RO
I −
=
∆t
 2 
O = CI + (1 − C )O
1
2
2
2
1
Subíndices 1 y 2 se refieren a valores
en el intervalo computacional ∆tt
1
Donde:
C=
2∆t
(2 R + ∆t )
77
Ecuación básica en el H.U.
sintético de Clark
O = CI + (1 − C )O
2
1
2 ∆t
C=
(2 R + ∆t )
•Se inicia el cálculo con la relación tiempo-area para generar I
•Con ∆t y R se calcula C
•En el inicio del cálculo, el gasto de salida es 0.0 ya que la lluvia inicial es
para infiltración y otras pérdidas.
78
EJEMPLO Clark U.H.
•
•
•
•
•
•
Area de la cuenca = 78 mi2
Tiempo de concentración = 8 horas
Constante de almacenamiento= 7.7 horas
Relación tiempo área dadas
∆t=1 hora
Se calcula C
C = 2 ∆t /( 2 R + ∆t ) = 2(1) /[( 2(7.7 ) + 1]
C = 0.122
O = 0.122 I + 0.878 O
i
i −1
79
Tabla Tiempo-Area
(Translado del Hidrograma)
TIEMPO AREA
(HORAS) (MI^2)
0
1
2
3
4
5
6
7
8
0.0
3.3
12.6
32.0
46.3
55.7
66.5
76.5
78.0
INCR. AREA HIDROGR.
HIDROGR.
(MI^2)
(MI^2-IN/HR) (CFS)
3.3
9.3
19.4
14.3
9.4
10.8
10.0
1.5
3.3
9.3
19.4
14.3
9.4
10.8
10.0
1.5
2130
6002
12519
9228
6066
6970
6453
968
80
Atenuación del Hidrograma
TIEMPO
(HORAS)
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
HIDR.
CI
(1-C)Oi-1
Oi
TRANSL. 0.122 I
0.878 Oi-1
(CFS)
0
0
0
2130
260
0
6002
732
228
12519
1527
843
9228
1126
2081
6066
740
2816
6970
850
3122
6453
787
3488
968
118
3754
0
0
3399
2985
2620
2301
2020
1774
1557
1367
1200
1054
1-hour UH
0
260
960
2371
3207
3556
3972
4275
3872
3399
2985
2620
2301
2020
1774
1557
1367
1200
1054
0
130
610
1665
2789
3382
3764
4124
4073
3635
3192
2803
2461
2160
1897
1665
1462
1284
1127
81
Como regla general…R??
Esto es lo real:
El parámetro requiere calibración (cuenca
instrumentada!) y su significado es más teórico
que físico
De acuerdo a Clark:
Se determina de registros de gastos a la salida de la
cuenca. Es igual al tiempo en el cual el decremento
de gastos a la salida es el más grande
82
Determinación de R
Calibrandolo con parámetros conocidos de
la cuenca
El determinado con cuenca instrumentada se puede
calibrar con parámetros conocidos y hacer
extensivo a cuencas similares. Ejem. En Illinois:
R = 1 . 64 L
0 . 342
S
− 0 . 790
R en horas
L = Longitud del canal principal en millas
S = Pendiente del canal principal, ft/milla
83
Determinación de R
(Requiere más comprensión de tránsito de
avenidas con Muskingum)
De acuerdo a Clark: Se determina de registros de
gastos a la salida de la cuenca y R se determina en
tiempo en el cual el decremento de gastos do/dt a
la salida es el más grande
O
R = −
dO / dt
84