GUIA-Relaciones Binarias.

Sean E y F no vacíos, se define una relación binaria en ExF,
tal que:
R= {( x, y) /( x, y ) ∈ ExF : x ∉ E ∧ y ∈ F }
Notación (x,y) ∈ R es lo mismo a escribir xRy . Esto se lee:”x
esta relacionado con y” o bien el par ordenado (x,y) pertenece a
la relación. Caso contrario se anotara:
o bien (x,y) ∉ R
Normalmente una relación se puede explicitar por extensión.
Ejemplo:
Si E= {x / x ∈ N : 2 < x < 8} , F= {x / x ∈ N : 1 < x ≤ 6}
En este caso E y F por extensión corresponden a:
E= {3,4,5,6,7} y F= {2,3,4,5,6}
Si en ella se define la relación R= {(3,4); (4,5); (5,6)} que esta expresada por
extensión.
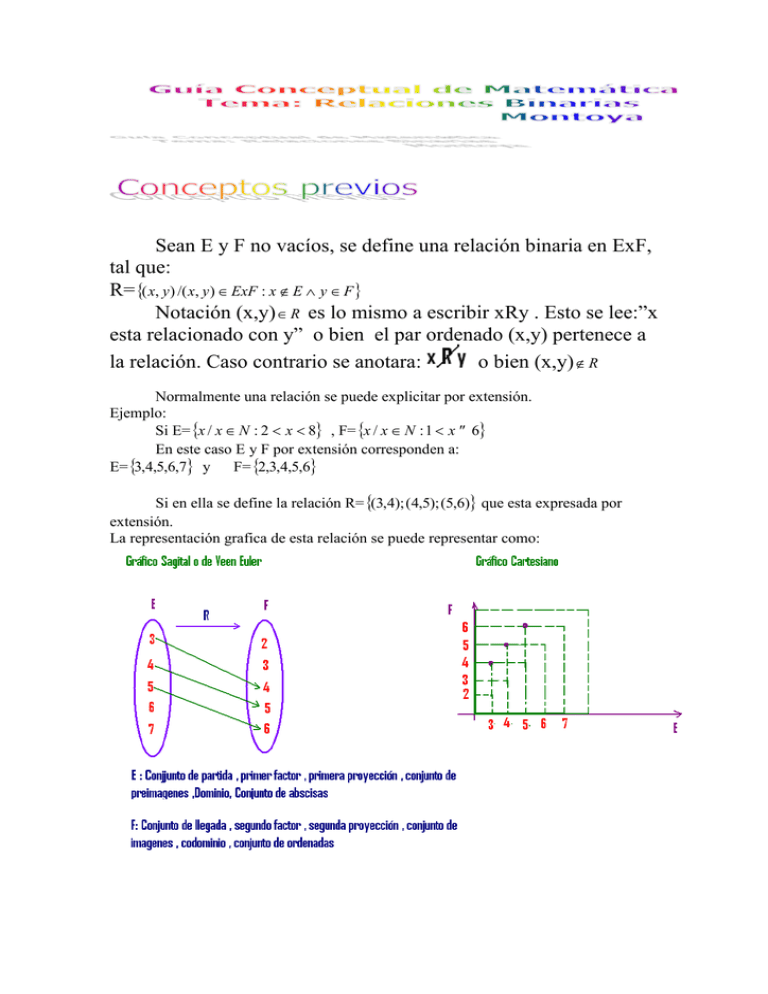
La representación grafica de esta relación se puede representar como:
Se define: Dom(R) = {x / ∀( x, y ) ∈ R}
.Es decir corresponde a las primeras
componentes de los pares ordenados que pertenecen a la relación
Para el ejemplo:
Dom(R)= {3,4,5}
Del mismo modo se define Rec(R)= {y / ∀( x, y ) ∈ R}.Es decir corresponden a
las segundas componentes de los parres ordenados que pertenecen a la relación.
Para el ejemplo:
Rec (R)= {4,5,6}
Esta misma relación se puede definir por comprensión, estableciendo una
relación matemática o ley de formación que se da entre loas componentes de los pares
ordenados.
Para el caso anterior, la ley de formación se puede establecer como:
R = {( x, y ) /( x, y ) ∈ ExF : y − x = 1}
LA RELACION NEGATIVA O COMPLEMENTARIA (R’ o bien R c ), que
se expresa simbólicamente como:
R’= {( x, y ) /( x, y ) ∈ ExF ∧ ∉ R}
En el ejemplo anterior:
(3,2), (3,3), (4,2), (4,3), (4,4), (4,6), (5,2), (5,3), (5,4),5,5), (6,2), (6,3), (6,4), (6,5), (6,6), (7,2), (7,3),
R' = 

(7,4), (7,5), (7,6)

Esta misma relación complementaria se puede abreviar por comprensión
“negando la ley de formación” que define la relación directa R, esto es:
R' = {( x, y ) /( x, y ) ∈ ExF : y − x ≠ 1}
LA RELACION INVERSA(R −1 ) : Se define simbólicamente como:
Sean E y F no vacíos, se define una relación directa, binaria en ExF, tal que:
R= {( x, y ) /( x, y ) ∈ ExF : x ∉ E ∧ y ∈ F } , entonces la inversa es:
R −1 = {( y, x) /( y, x) ∈ FxE ⇔ ( x, y ) ∈ R}
Para el ejemplo anterior
R −1 = {(4,3), (5,4), (6,5)}
Esta misma relación se puede escribir por comprensión como
R = {( x, y ) /( x, y ) FxE : x − y = 1}
−1
OBS: El Dominio de la relación directa equivale al Recorrido de
la Inversa y viceversa
EJERCICIOS DE APLICACIÓN:
1.- Dados: E = {x / x ∈ ℵ : 6 ≤ x < 10} y F= {x / x ∈ ℵ : 3 ≤ x < 12} , en ExF se definen
las relaciones: R 1 {( x, y ) /( x, y ) ∈ ExF : x + y = 15}
R 2 {( x, y ) /( x, y ) ∈ ExF : 2 x + y = 10}
R 3 {( x, y ) /( x, y ) ∈ ExF : x + y > 12}
R 4 {( x, y ) /( x, y ) ∈ ExF : x + 2 y = 12}
R 5 {( x, y ) /( x, y ) ∈ ExF : x − y = 0}
R 6 {( x, y ) /( x, y ) ∈ ExF : x = 2n, n = 1,2,3,. y = 3}
Para cada una de estas relaciones encuentre:
1.1.- La relación por extensión.
1.2.- La cardinalidad
1.3.- El dominio de definición.
1.4.- El dominio de imágenes.
1.5.- El grafico cartesiano
1.6.- El grafico sagital
1.6.- La relación inversa .por extensión y comprensión
1,7,. La relación complementaria por extensión y comprensión.
2.- Si E = {x / x ∈ ℵ : 1 < x ≤ 15}.Se definen en ExE las relaciones:
R 1 {( x, y ) /( x, y ) ∈ ExE : 2 x + 3 y = 24}
R 2 {( x, y ) /( x, y ) ∈ ExE : 2 x = y}
R 3 {( x, y ) /( x, y ) ∈ ExE : x + 2 y ≥ 45}
R 4 {( x, y ) /( x, y ) ∈ ExE : x − y = 0}
Para cada una de las relaciones determine :
2.1.- La relación por extensión.
2.2.-La cardinalidad.
2.3.- El dominio de definición .
2.4.- El dominio de imágenes.
2.5.- El grafico cartesiano
2.6.- El grafico sagital
2.6.- La relación inversa .por extensión y comprensión
2,7,. La relación complementaria por extensión y comprensión.
2.8.- La relaciones que son reflexivas.
2.9.-Las relaciones que son simétricas.
2.10.-Las relaciones que son transitivas.
2.11.-Las relaciones de equivalencias.
3.-Explique por que las siguientes relaciones son de equivalencias.
3.1.-La relación de igualdad.
3.2.- La relación de congruencia entre figuras geométricas.
3.3.-La relación de semejanza entre triángulos.
3.4.-La relación de equivalencias entre figuras geométricas.
4.- Si E= E = {x / x ∈ ℵ : 1 ≤ x ≤ 10} y F= E = {x / x ∈ ℵ : x < 8}.
Se definen: R 1 {( x, y ) /( x, y ) ∈ ExF : 3x + 2 y = 24}
R 2 {( x, y ) /( x, y ) ∈ FxE : x − y = 0}
R 3 {( x, y ) /( x, y ) ∈ FxF : x + y > 15}
R 4 {( x, y ) /( x, y ) ∈ ExE : 2 x − y = 0}
R 5 {( x, y ) /( x, y ) ∈ ExF : x + y < 2}
Determine.
4.1.- Cada una de las relaciones por extensión.
4.2.- Clasifique las relaciones según sus propiedades.
4.3.- ¿Hay alguna de ellas que corresponda a una relación Universal?
4.4.-¿Hay alguna de ellas que corresponda a una relación vacía?
5.- Para cada uno de los gráficos que se indican .determine:
5.1.- El conjunto de partida y el de llegada (primer y segundo factor) por extensión.
5.2.- Cada una de las relaciones en notación conjuntita.
5.3.-El dominio de preimagenes y el dominio de imágenes de cada una de las relaciones.