Ejercicio nº 1.- Desarrolla y simplifica: Ejercicio nº 2.
Anuncio

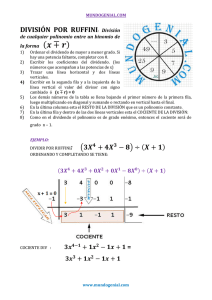
Ejercicio nº 1.- Desarrolla y simplifica: Ejercicio nº 2.- Dado el polinomio P(x) 4x 3 8 x 2 3x 1: a) Halla el cociente y el resto de la división: b) ¿Cuánto vale P(2)? Ejercicio nº 3.- Descompón en factores los siguientes polinomios: a) x 3 13x 2 36x b) 2x 3 9x 2 8x 15 Ejercicio nº 4.- Descompón en factores el dividendo y el divisor, y luego simplifica: Ejercicio nº 5.- Calcula y simplifica: Ejercicio nº 6.- Traduce al lenguaje algebraico empleando una sola incógnita: a El área de un rombo cuyas diagonales suman 46 cm. b Una cantidad x aumentada un 25%. c El producto de dos números cuya diferencia es 9. d La diferencia de precio que habría entre alquilar un autobús por 540 € x estudiantes o seis menos. Ejercicio nº 7.- Calcula un polinomio que dividido por 3x 1 de x2 2x 1 de cociente dejando un resto de 5 unidades. Ejercicio nº 8.- Simplifica la siguiente fracción algebraica: Soluciones: Matemáticas, opción B Opción C Educación Secundaria 4 SOLUCIONES Evaluación: ............................................................................................................................................. ...... Fecha: .............. Ejercicio nº 1.- Desarrolla y simplifica: Solución: Ejercicio nº 2.- Dado el polinomio P(x) 4x 3 8 x 2 3x 1: a) Halla el cociente y el resto de la división: b) ¿Cuánto vale P(2)? Solución: a) Aplicamos la regla de Ruffini: 2 4 8 8 4 0 3 0 3 1 6 5 Cociente 4x 2 3 Resto 5 b) Por el teorema del resto, sabemos que P(2) 5. Ejercicio nº 3.- Descompón en factores los siguientes polinomios: a) x 3 13x 2 36x b) 2x 3 9x 2 8x 15 Solución: a) Sacamos factor común y hallamos las otras raíces resolviendo la ecuación de segundo grado: Por tanto: x 3 13x 2 36 x x x 9 x 4 b) Utilizamos la regla de Ruffini: 1 5 2 9 8 15 2 7 15 2 7 15 0 10 15 2 3 0 2x 3 9x 2 8x 15 x 1 x 5 2x 3 Ejercicio nº 4.- Descompón en factores el dividendo y el divisor, y luego simplifica: Solución: En el primer paso sacamos factor común y en el segundo paso aplicamos el producto notable a2 b2 a b a b a la expresión x4 1. Ejercicio nº 5.- Calcula y simplifica: Solución: b) Efectuamos el cociente: Factorizamos para simplificar: x 2 25 (x - 5) (x 5) Producto notable 2x 10 2(x 5) x2 6x 9 (x 3)2, ya que las raíces de x2 6x 9 0 son: x2 2x 15 (x 5) (x 3), ya que las raíces de x2 2x 15 0 son: Así: Ejercicio nº 6.- Traduce al lenguaje algebraico empleando una sola incógnita: a El área de un rombo cuyas diagonales suman 46 cm. b Una cantidad x aumentada un 25%. c El producto de dos números cuya diferencia es 9. d La diferencia de precio que habría entre alquilar un autobús por 540 € x estudiantes o seis menos. Solución: b 1,25x c Los números son x y 9 x Producto x (9 x 9x x2 Ejercicio nº 7.- Calcula un polinomio que dividido por 3x 1 de x2 2x 1 de cociente dejando un resto de 5 unidades. Solución: Hemos de calcular D(x), polinomio dividendo, conocido el divisor d(x) 3x 1, el cociente c(x) x2 2x 1 y el resto r 5. Ejercicio nº 8.- Simplifica la siguiente fracción algebraica: Solución: