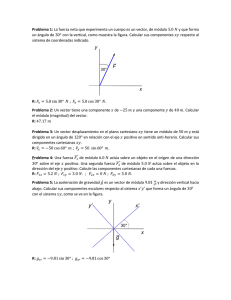
Movimiento circular desplazado del origen.
Anuncio

Movimiento circular desplazado del origen. Hasta ahora sólo hemos estudiado movimiento circular cuando el origen, o punto de referencia, está situado en el centro del círculo. Pero ¿qué pasa cuando el marco preferencial no se encuentra ahí? Entonces tenemos una situación como la que se ilustra en la siguiente figura: y ϕ r a θ x Como puede observarse, hay dos ángulos, uno para el movimiento circular y otro que es el ángulo propio del vector posición con respecto al marco de referencia. Sabemos que si estamos parados en el centro del círculo, el vector de posición tiene la forma: x = r cos φ iˆ + sin φ ˆj ( ) Pero si el círculo está fijo en una posición diferente al origen (desplazado por un vector a ), entonces el vector posición está dado por: ( ) x = r cos φ iˆ + sin φ ˆj + a = ( r cos φ + ax ) iˆ + ( r sin φ + a y ) ˆj ¨ Por lo tanto el ángulo, con respecto al marco de referencia no es ϕ sino θ, el cual se calcula: r sin φ + a y r cos φ + ax θ = arctan En el problema del golfista si ponemos al marco de referencia como la pelota, entonces el círculo que describe el palo estará centrado en: a = rjˆ Ya que el círculo está directamente sobre la pelota y la circunferencia se dibuja hasta el suelo. Entonces la dificultad aquí es reconocer qué parte del movimiento se lleva a cabo en el círculo que describe el palo de golf, y por lo tanto qué valores son los que afectan a ϕ. Y después obtener un valor para θ que será el ángulo para el disparo en tiro parabólico.