Encontrar la ecuación de la parábola que tiene su vertice en el punto
Anuncio

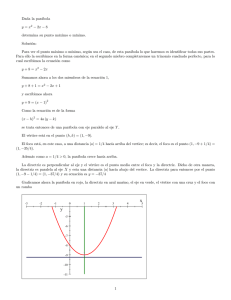
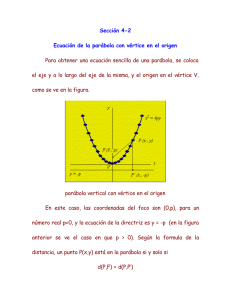
Encontrar la ecuación de la parábola que tiene su vertice en el punto ( 1; 4), el eje focal es vertical y pasa por el punto (2; 2). Solución: La ecuación de una parábola con vertice en (h; k) y foco en (h; k + a) es (x 2 h) = 4a (y k). En este caso, el vertice está en ( 1; 4), así que h = 1 y k = 4. Para encontrar a, usamos el que el punto (2; 2) está sobre la parábola, por tanto, se debe cumplir 2 (2 + 1) = 4a (2 4) o sea 8a + 9 = 0 que nos da a= 9 8 Por tanto, la ecuación de la parábola es 9 8 2 (x + 1) = 4 (y 4) que se reduce a 2x2 + 4x + 9y 34 = 0 La grá…ca de esta parábola es y 5 4 3 2 1 -8 -7 -6 -5 -4 -3 -2 -1 1 2 -1 -2 -3 -4 -5 El punto (2; 2) está marcado por una pequeña cruz azul. 1 3 4 5 x