Encontrar la ecuación de una parábola dado el foco y su directriz Ej. 1

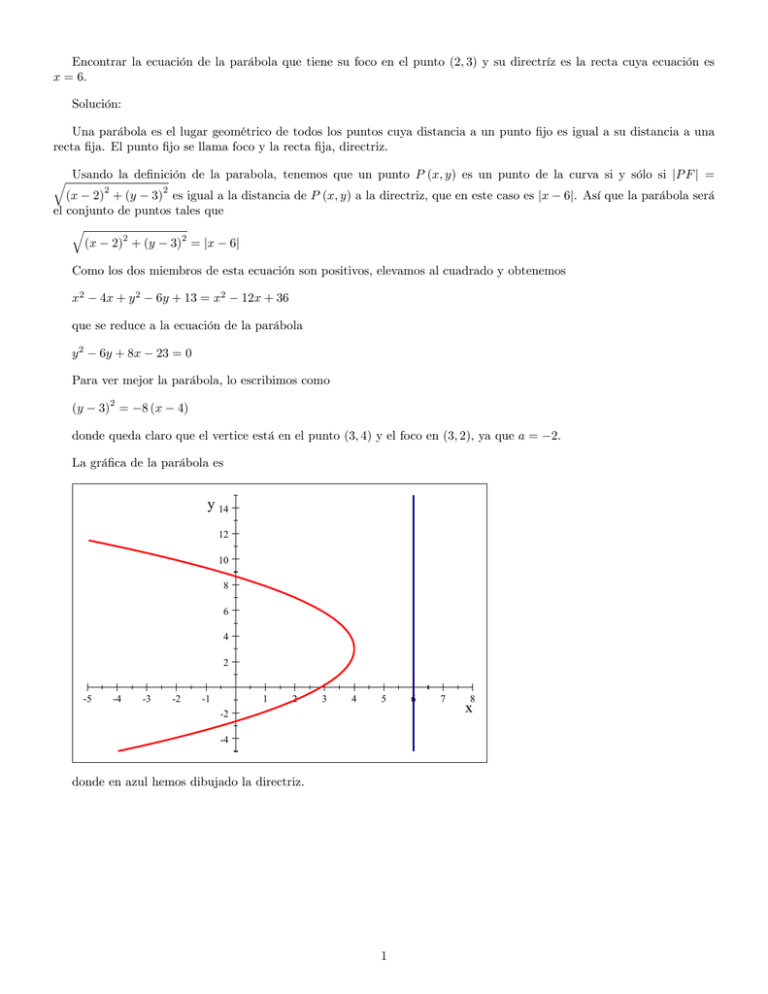
Encontrar la ecuación de la parábola que tiene su foco en el punto (2; 3) y su directríz es la recta cuya ecuación es
x = 6.
Solución:
Una parábola es el lugar geométrico de todos los puntos cuya distancia a un punto …jo es igual a su distancia a una
recta …ja. El punto …jo se llama foco y la recta …ja, directriz.
q Usando la de…nición de la parabola, tenemos que un punto P (x; y) es un punto de la curva si y sólo si jP F j =
2
2
(x 2) + (y 3) es igual a la distancia de P (x; y) a la directriz, que en este caso es jx 6j. Así que la parábola será
el conjunto de puntos tales que
q
2
2
(x 2) + (y 3) = jx 6j
Como los dos miembros de esta ecuación son positivos, elevamos al cuadrado y obtenemos
x2
4x + y 2
6y + 13 = x2
12x + 36
que se reduce a la ecuación de la parábola
y2
6y + 8x
23 = 0
Para ver mejor la parábola, lo escribimos como
2
(y
3) =
8 (x
4)
donde queda claro que el vertice está en el punto (3; 4) y el foco en (3; 2), ya que a =
La grá…ca de la parábola es
y 14
12
10
8
6
4
2
-5
-4
-3
-2
-1
1
2
3
4
5
-2
-4
donde en azul hemos dibujado la directriz.
1
6
7
8
x
2: