Departamento de Física Aplicada III Universidad de Sevilla
Anuncio
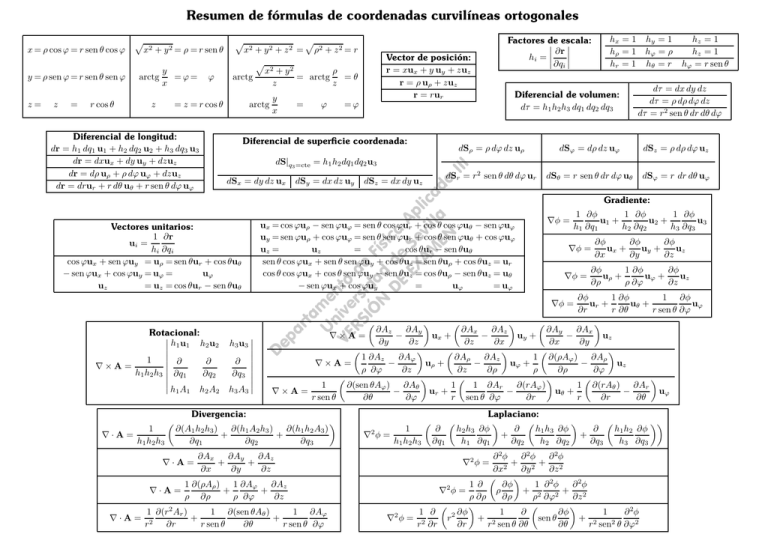
Resumen de fórmulas de coordenadas curvilı́neas ortogonales = r cos θ z ϕ y arctg x = z = r cos θ Diferencial de longitud: dr = h1 dq1 u1 + h2 dq2 u2 + h3 dq3 u3 dr = dxux + dy uy + dzuz dr = dρ uρ + ρ dϕ uϕ + dzuz dr = drur + r dθ uθ + r sen θ dϕ uϕ ∇·A= 1 h1 h2 h3 dSx = dy dz ux 2 dSρ = ρ dϕ dz uρ h3 u3 ∂ ∂q3 h A 3 dSr = r2 sen θ dθ dϕ ur dSz = dx dy uz 3 hx = 1 hy = 1 hρ = 1 hϕ = ρ hr = 1 hθ = r Diferencial de volumen: dτ = h1 h2 h3 dq1 dq2 dq3 hz = 1 hz = 1 hϕ = r sen θ dτ = dx dy dz dτ = ρ dρ dϕ dz dτ = r2 sen θ dr dθ dϕ dSϕ = dρ dz uϕ dSz = ρ dρ dϕ uz dSθ = r sen θ dr dϕ uθ dSϕ = r dr dθ uϕ Gradiente: ux = cos ϕuρ − sen ϕuϕ = sen θ cos ϕur + cos θ cos ϕuθ − sen ϕuϕ uy = sen ϕuρ + cos ϕuϕ = sen θ sen ϕur + cos θ sen ϕuθ + cos ϕuϕ uz = uz = cos θur − sen θuθ sen θ cos ϕux + sen θ sen ϕuy + cos θuz = sen θuρ + cos θuz = ur cos θ cos ϕux + cos θ sen ϕuy − sen θuz = cos θuρ − sen θuz = uθ − sen ϕux + cos ϕuy = uϕ = uϕ ∇φ = 1 ∂φ 1 ∂φ 1 ∂φ u1 + u2 + u3 h1 ∂q1 h2 ∂q2 h3 ∂q3 ∇φ = ∇φ = ∂φ ∂φ ∂φ ux + uy + uz ∂x ∂y ∂z ∂φ 1 ∂φ ∂φ uρ + uϕ + uz ∂ρ ρ ∂ϕ ∂z ∂φ 1 ∂φ 1 ∂φ ur + uθ + uϕ ∂r r ∂θ r sen θ ∂ϕ ∂Ay ∂Az ∂Ax ∂Az ∂Ax ∂Ay − ux + − uy + − uz ∇×A= ∂y ∂z ∂z ∂x ∂x ∂y ∂Aϕ ∂Az 1 ∂(ρAϕ ) ∂Aρ 1 ∂Az ∂Aρ − uρ + − uϕ + − uz ∇×A = ρ ∂ϕ ∂z ∂z ∂ρ ρ ∂ρ ∂ϕ ∂(rAϕ ) 1 1 1 ∂(rAθ ) ∂Ar ∂(sen θAϕ ) ∂Aθ 1 ∂Ar − ur + − uθ + − uϕ ∇×A= r sen θ ∂θ ∂ϕ r sen θ ∂ϕ ∂r r ∂r ∂θ ∂(A1 h2 h3 ) ∂(h1 A2 h3 ) ∂(h1 h2 A3 ) + + ∂q1 ∂q2 ∂q3 ∇·A= ∇·A= 2 dSy = dx dz uy Divergencia: ∇·A= =ϕ dS|q3 =cte = h1 h2 dq1 dq2 u3 Rotacional: h1 u1 h2 u2 ∂ 1 ∂ ∇×A = h1 h2 h3 ∂q1 ∂q2 h A h A 1 ϕ Diferencial de superficie coordenada: Vectores unitarios: 1 ∂r ui = hi ∂qi cos ϕux + sen ϕuy = uρ = sen θur + cos θuθ − sen ϕux + cos ϕuy = uϕ = uϕ uz = uz = cos θur − sen θuθ 1 = Factores de escala: ∂r hi = ∂qi III z y =ϕ= x Vector de posición: r = xux + y uy + zuz r = ρ uρ + zuz r = rur rt am U e n VE ive nto RS rs de IÓ ida F N d ísi DE de ca EX Se Ap AM vil lic EN la ada z= arctg x2 + y 2 + z 2 = ρ2 + z 2 = r ρ x2 + y 2 = arctg =θ arctg z z ∇φ = pa y = ρ sen ϕ = r sen θ sen ϕ x2 + y 2 = ρ = r sen θ De x = ρ cos ϕ = r sen θ cos ϕ ∂Ay ∂Az ∂Ax + + ∂x ∂y ∂z ∂Az 1 ∂(ρAρ ) 1 ∂Aϕ + + ρ ∂ρ ρ ∂ϕ ∂z 1 ∂(sen θAθ ) 1 ∂Aϕ 1 ∂(r2 Ar ) + + r2 ∂r r sen θ ∂θ r sen θ ∂ϕ ∇2 φ = 1 h1 h2 h3 ∂ ∂q1 Laplaciano: ∂ ∂ h2 h3 ∂φ h1 h3 ∂φ h1 h2 ∂φ + + h1 ∂q1 ∂q2 h2 ∂q2 ∂q3 h3 ∂q3 ∂ 2φ ∂ 2φ ∂ 2φ + 2 + 2 ∂x2 ∂y ∂z ∂φ 1 ∂ 2φ 1 ∂ ∂ 2φ ρ + 2 ∇2 φ = + ρ ∂ρ ∂ρ ρ ∂ϕ2 ∂z 2 1 ∂φ 1 1 ∂ ∂φ ∂ ∂ 2φ r2 + 2 sen θ + 2 ∇2 φ = 2 2 r ∂r ∂r r sen θ ∂θ ∂θ r sen θ ∂ϕ2 ∇2 φ =

