Ejercicios 09
Anuncio
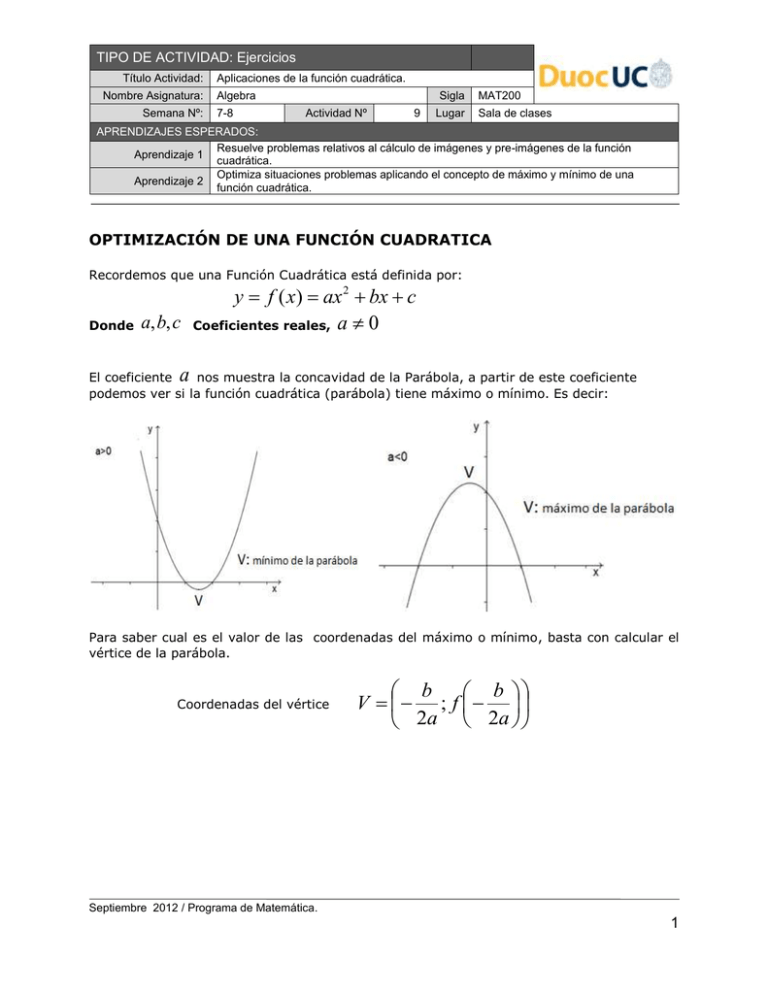
TIPO DE ACTIVIDAD: Ejercicios Título Actividad: Nombre Asignatura: Semana Nº: Aplicaciones de la función cuadrática. Algebra 7-8 Sigla Actividad Nº 9 Lugar MAT200 Sala de clases APRENDIZAJES ESPERADOS: Resuelve problemas relativos al cálculo de imágenes y pre-imágenes de la función Aprendizaje 1 cuadrática. Optimiza situaciones problemas aplicando el concepto de máximo y mínimo de una Aprendizaje 2 función cuadrática. OPTIMIZACIÓN DE UNA FUNCIÓN CUADRATICA Recordemos que una Función Cuadrática está definida por: Donde y f ( x) ax 2 bx c a, b, c Coeficientes reales, a 0 a El coeficiente nos muestra la concavidad de la Parábola, a partir de este coeficiente podemos ver si la función cuadrática (parábola) tiene máximo o mínimo. Es decir: Para saber cual es el valor de las coordenadas del máximo o mínimo, basta con calcular el vértice de la parábola. Coordenadas del vértice b b V ; f 2a 2a Septiembre 2012 / Programa de Matemática. 1 I. Optimice los siguientes ejercicios 1. En una empresa agrícola, la utilidad (en miles de dólares) al vender tractores agrícolas está dada por la función, x repuestos para U( x ) = 6 x 132x . Encontrar la 2 cantidad de repuestos que se deben vender para obtener la máxima utilidad. ¿A cuánto haciende esa máxima utilidad? 2. La cantidad de kilómetros que una moto puede recorrer por litro de bencina a una velocidad v (km/hrs), está dada por la función, K( v ) = 0,8v v2 . ¿Cuál es la 250 velocidad que maximiza el rendimiento de la moto? Es decir encuentre la mayor cantidad de kilómetros como de velocidad, con un litro de bencina. 3. En la casa de la construcción, el costo de la madera a utilizar (en cientos de pesos) por unidad al producir x casas prefabricadas está dado por la función, C( x ) = x 2 180x 20.000. Encontrar la cantidad de casas prefabricadas que minimizan el costo en madera por unidad. ¿Cuánto es el costo mínimo de madera a utilizar? 4. Un contador, estima que sus ingresos mensuales al llevarle la contabilidad a ciertos microempresarios están dados por la función I(c)= 1.200.000 1.000c 2c , donde c es la cantidad de microempresarios que le lleva la contabilidad en el mes. ¿A qué cantidad de microempresarios debe llevarle la contabilidad mensualmente para obtener el mayor ingreso? Y ¿Cuál será su ingreso máximo? 2 5. En una empresa que era exitosa y donde el personal iba creciendo a medida que transcurría el tiempo, los recursos comenzaron a escasear y el personal decreció. El número de trabajadores a los t años de haber creado la empresa está dado por, 2 p(t)= t 22t 112, (t >0). Determine la cantidad de años donde hubo mayor cantidad de trabajadores. ¿Cuál fue la mayor cantidad de trabajadores que logro tener la empresa? 6. La pastoral juvenil de DuocUC organizó un partido de fútbol. Durante el partido, un jugador le da un puntapié a la pelota, tal que la trayectoria de esta queda expresada por la función, h( x ) = 5t 20t 1 , donde h es la altura en metros y t es el tiempo en seg. Determine el tiempo en que la pelota alcanza la altura máxima. ¿Qué altura alcanzó? 2 Septiembre 2012 / Programa de Matemática. 2 INTERSECCIÓN DE FUNCIONES Intersección entre función cuadrática y lineal Sean las funciones f ( x) ax bx c y 2 f ( x) mx n La intersección de estas se puede apreciar en la grafica Donde los puntos Ay B se obtienen igualando las funciones y resolviendo la ecuación: ax2 bx c mx n px2 qx r 0 Donde 𝑝𝑥 2 + 𝑞𝑥 + 𝑟 = 0 es una ecuación de segundo grado, y sus soluciones las encontramos + Con la formula general 𝑥= −𝑞 −√𝑞 2 −4∙𝑝∙𝑟 2∙𝑝 . Septiembre 2012 / Programa de Matemática. 3 II. Analice la intersección de los siguientes ejercicios 7. En una empresa, recursos humanos determinó que el bono de Navidad para este año 2012 dependerá de los años de antigüedad y además del cargo que desempeñan. Para los administrativos su bono se calculará según la fórmula para los cargos superiores según BSup (t ) 26 t 16 BAdm (t ) 4 t 3 t 2 y donde t son los años y B el bono en miles de pesos. a. ¿Habrá algún año de antigüedad tal que el valor de ambos bonos sea el mismo? b. A los 15 años de antigüedad, ¿Quienes obtienen un mejor bono de Navidad? 8. Un grupo de trabajadores de una empresa logran fabricar P1 (t ) t 2 2 t artículos de aseo en t días y otro grupo de igual número de trabajadores fábrica P2 (t ) 4 t 16 artículos en t días. a. ¿Habrá alguna cantidad de días el cuál la producción sea la misma? b. ¿Cuál es esa producción? 9. Dos tasadores utilizan distinta fórmula para la depreciación (perdida de valor) de una maquinaria pesada. El primero utiliza la función cuadrática V1 (t ) 0,2 t 2 2,6 t 10,4 y el otro tasador la función lineal V2 (t ) 1,2 t 9,2 , donde t está en años y V el valor de la máquina en millones de pesos. Considerando t mayor a 1 año. ¿A los cuántos años el valor de ambas tasaciones es de igual valor? 10. La ganancia G (en dólares) de una cadena de comida rápida al vender x hamburguesas semanales viene dado por G 2,44 x x2 2.006 ¿Cuál es la 20.000 menor cantidad de hamburguesas que habrá que vender a la semana para obtener una ganancia de 4.000 dólares? 11. Hoy, el número de habitantes de dos localidades del Sur de Chile crece según los modelos P1 (t ) 80 t 12.500 y P2 (t ) t 2 72 t 12.480 donde t se mide en años. ¿En cuánto años más el número de habitantes de ambas localidades será la misma? 12. Se desea pedir un crédito de $ 20.000.000 en 2 instituciones financieras. Una de ella I1 (t ) 0,06 t 2,434 y la otra calcula la tasa de interés según I 2 (t ) 0,006 t 2 0,02 t 2,49 donde t es el número de meses al cuál se pedirá el crédito. ¿A cuántos meses habrá que tomar el crédito para que la tasa de interés sea la misma? Septiembre 2012 / Programa de Matemática. 4 SOLUCIONES 1. 11 Repuestos y la utilidad máxima haciende a 726.000 dólares. 2. La velocidad máxima es de 100 km/hrs. Y recorre 40 km. Con un litro. 3. 90 casas y el costo mínimo en madera a utilizar es de 1.190.000 pesos. 4. 250 microempresarios y su ingreso máximo será de 1.325.000 pesos. 5. 11 años y la mayor cantidad de trabajadores que tubo la empresa fue de 233. 6. A los 2 segundos, y alcanzó 21 metros. 7. a. 8 años b. El mejor Bono lo tienen los Administrativos $279.000 8. a. 8 días b. 48 artículos 9. A los 6 años 10. 2600 hamburguesas 11. A los 10 años 12. A los 14 meses Septiembre 2012 / Programa de Matemática. 5