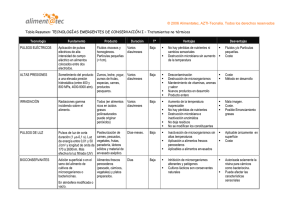
técnicas de interpolación de pulsos

INCERTIDUMBRE DEBIDO A LAS
TÉCNICAS DE INTERPOLACIÓN DE PULSOS USADAS
EN UN PROBADOR COMPACTO
(COMPARACIÓN DE LAS TÉCNICAS DE DOBLE Y CUADRUPLE CRONOMETRIA).
José Lara Manríquez
Centro Nacional de Metrología
Apdo. Postal 1 – 100 CP 76241 Querétaro, México. 2000-2003
jlara@cenam.mx
Resumen:
En los trabajos de calibración de los sistemas de medición de flujo del tipo turbina u
otros tipos de medidores en línea, que manejen como señal de salida un tren de pulsos,
empleando como referencia un probador compacto --que además emplea la técnica de
doble cronometría para interpolar los pulsos del medidor bajo calibración-- ( obtener la
fracción de pulso que no se contabiliza en los indicadores de pulsos en el proceso de
calibración), el CENAM ha efectuado un trabajo de investigación cuyo objetivo es
comparar el desempeño por el uso de las técnicas de interpolación de pulsos.
En este trabajo se presentan los resultados de las dos técnicas de interpolación de pulsos
y la comparación respecto de su contribución en los resultados de calibración en medidores de flujo tipo turbina y la influencia de las técnicas de interpolación de pulsos en la
incertidumbre de la medición del factor k del medidor.
Noviembre 2001
Introducción
En 1978 el interés en la mejora continua
de los probadores convencionales, de la
empresa Flow Technology se introduce
un nuevo concepto, el probador compacto, que era de un orden de magnitud
más pequeño comparable con cualquier
probador en ese tiempo, logrando hacer
esto con el uso de nuevas tecnologías
aplicadas a este proyecto. El probador
constituía en si de cuatro sistemas novedosos, el uso de un sistema hidráulico
que retornaba en contra flujo un pistón
alojado en un cilindro, una cámara separada para la zona de medición, la cual
mediante fotosensores de alta exactitud
definían la posición del pistón en el cilindro, un sistema neumático que propiciaba el cierre de un válvula en el interior de un cilindro y un sistema antibloqueo de conjunto pistón y válvula (válvula póppet); que garantizaba que el
fluido de calibración no interrumpía su
paso a través del probador en ningún
instante.
Principio de Operación.
Constitución física: El probador compacto consta de una sección recta de
tubo (cilindro), de mayor diámetro que
el diámetro de entrada al probador
(diámetro cilindro ≈ ≥ 2 veces el diámetro nominal del probador), esto debido a
que en él se aloja un conjunto pistón y
válvula de características especiales,
que dado un instante abrirá permitiendo
reducidamente circular el fluido a través
del cilindro.
Fuera del pistón y en posición lineal al
cilindro se ubica una sección que está
constituida por una barra delgada, la
cual a un extremo está conectada al pistón que se desplaza dentro del cilindro;
en el otro lado de la barra esta fuertemente sujetada una lengüeta que simu-
laría una bandera y su asta. Paralelo a la
barra que fija la “bandera” están varios
sensores ópticos instalados en un soporte, los cuales detectan el paso de la bandera a través de ellos, en su recorrido
propiciado por el desplazamiento del
conjunto pistón válvula.
Fuera también del probador y en posición lineal y al centro del cilindro, se
encuentra una cámara que aloja el eje
principal sobre el cual se soporta el
arreglo pistón válvula, este eje como se
indica en un extremo esta fijo al arreglo
de pistón-válvula y en el otro lado se
tiene instalado un segundo pistón comparativamente de dimensiones pequeñas, el cual por uno de sus lados esta
sometido a una presión hidráulica y por
el otro a una presión neumática.
Operación: El probador compacto en
“Estado Inicial”, al derivar el fluido a
través de él, el pistón se aloja al final
del cilindro que lo contiene, esto propiciado por la velocidad del fluido de calibración que a través del cilindro. Aquí
la válvula poppet permanece abierta
gracias a un sistema de seguridad mecánico.
Cuando el sistema se pone en “Estado
de Listo” el conjunto pistón válvula es
llevado en contra flujo hasta la posición
de inicio del cilindro gracias a un sistema hidráulico, aquí el sistema mecánico
que propiciaba el que la válvula poppet
permaneciera abierta cesa más no se
cierra la válvula poppet debido a el contra flujo del fluido en calibración.
El “Estado de Calibrando” se logra
cuando en el control del probador se da
la orden de iniciar calibración, esto ocasiona la liberación del sistema hidráulico y a su vez la liberación del conjunto
pistón válvula y el cierre de esta última
propiciado por el sistema alterno neumático y el fluido de calibración.
En el “Estado de Calibrando” los sensores son cortados debido a que el pistón
desplaza consigo la “bandera”, mediante la barra que sujeta a ambos, obteniendo así el volumen del medidor, mediante la colección de los pulsos generados por el medidor correspondientes
al tiempo transcurrido entre el corte de
los sensores para los cuales se tiene el
volumen certificado del cilindro.
Tema de discusión
En el proceso de conteo de pulsos en los
trabajos de calibración, usando un probador compacto, los contadores que se
encargan de esta tarea ocasionan un
error de redondeo de ± 1 pulso debido a
la naturaleza de su función; y esto porque al iniciar la pasada en el probador
(corte del primer sensor). También se
inicia el conteo de los pulsos del medidor, pero la cuenta permanece inmóvil
hasta la aparición del estado de ascenso
(o descenso según configuración) del
tren de pulsos del medidor, lo mismo
ocurre al sensar el paso de la bandera
por el último sensor (término de la pasada), de tal manera que al inicio y final
se desconoce la fracción de pulso contabilizado, o no contabilizado, respectivamente.
Para estimar la fracción de pulso contabilizado existen técnicas que obtienen
esta fracción de pulso y así corregir o
complementar el totalizador de pulsos.
En la contabilización de pulsos por unidad de volumen, el diseño de probadores se realizaba para obtener un valor de
incertidumbre inferior a 0.01% (regla de
los 10 000 pulsos por pasada API 4),
esto significaba grandes dimensiones en
los probadores.
Con las técnicas de interpolación de
pulsos, introducidas en los probadores
de volumen pequeño, el objetivo de
lograr esta incertidumbre por manejo de
la señal de pulsos fue más que alcanzable (usando contadores con una resolución mejor que 0.000 05 partes del
tiempo de una pasada para evitar un
error de redondeo mayor 0.01% ISO
7278).
El uso de estas técnicas se extendió asta
los probadores convencionales donde se
podía tener una cantidad de pulsos por
corrida inferior a 10 000.
Técnica de doble cronometría. Esta
técnica se basa en el hecho de que la
señal de pulsos es continua y con un
periodo constante en el tren de pulsos,
esto es la mayoría de las veces imposible de lograr, dado el principio de funcionamiento de los probadores.
Esta técnica es la más usada, se emplean
dos contadores para contabilizar los
tiempos t1 y t2 como se muestra en la
figura 1, donde t1 mide el intervalo del
sensor óptico de inicio asta el segundo
sensor óptico., t2 mide el intervalo de
tiempo entre el primer pulso, una vez
cortado el primer sensor, y el primer
pulso una vez cortado el segundo sensor.
Un tercer contador totaliza el número
entero de pulsos por pasada del probador.
Usando la relación de tiempos podemos
obtener el número de pulsos interpolado
de la manera siguiente:
Ń=N
t1
t2
Donde:
Ń, Es el numero de pulsos interpolados,
N, Es el numero de pulsos enteros,
t1, Es el tiempo entre sensores ópticos y
t2, Es el tiempo transcurrido para el
conteo del numero de pulsos completos.
t1, Es el tiempo entre el corte del
sensor inicial y la aparición del primer pulso,
t2, Es el periodo del pulso en que es
cortado el sensor inicial.
Pulsos del
medidor
t1
t3, Es el tiempo entre el corte del
sensor final y la aparición del primer
pulso,
t2
Señal del
primer sensor
t4, Es el periodo del pulso en que es
cortado el sensor final.
Señal del
segundo sensor
Figura 1. Tiempos para doble cronometría
Técnica de cuádruple cronometría. Si
el objeto de medir la fracción del pulso
que ocurre en cada extremo de la corrida de calibración, entonces si medimos
esas fracciones de pulso mencionadas
tendremos una mejor estimación de estas con la técnica de cuádruple cronometría.
Esta técnica es poco usada hasta ahora
por el costo considerable que hasta en
ese entonces resultaba instrumentar un
equipo que realizara la toma de tiempo
del periodo de un ciclo de pulso que era
identificado hasta que era señalado por
el corte del primer sensor óptico. Cuatro
contadores son usados en este método y
su distribución esta descrita en la figura
2, y el cálculo del número de pulsos
interpolado esta dado por la relación
siguiente.
Ń=N+
t1 t3
t2 t4
Donde:
Ń, Es el numero de pulsos interpolados,
N, Es el numero de pulsos enteros,
t2
t1
Señal del
primer sensor
t4
Pulsos del
medidor
t3
Señal del
segundo sensor
Figura 2. Distribución de Tiempos
para cuádruple cronometría.
Técnica de enganche en la fase del
pulso.
El principio de esta técnica difiere de
las otras totalmente dado que en esta se
basa en un multiplicador de pulsos
constante el cual su salida es sustituida
por el tren de pulsos del medidor que es
contabilizado por el totalizador del probador.
Esta técnica es quizá la más sencilla y la
menos usada dado el problema de que
para poder garantizar una buena interpolación el tren de pulsos del medidor
debe de garantizar que su periodo no
cambia repentinamente y esto es impredecible por el proceso mismo de que se
trata.
En la figura 3 se muestra el diagrama de
bloques para esta técnica de interpolación de pulsos, donde el resultado de
pulsos interpolados es obtenido de la
manera siguiente.
Ń=
N
R
Donde:
Ń, Es el numero de pulsos interpolados,
N, Es el numero de pulsos generados
por el oscilador y,
R, Es el factor de multiplicación utilizado por el oscilador en la figura 3.
Señal del
primer sensor
Señal del
segundo sensor
Pulsos del
medidor
Comparador de
fase
Oscilador
de voltaje
regulado
1
R
Figura 3. Proceso de la técnica de
enganche de fase para interpolación de pulsos
Tema de discusión.
Desde hace varios años en el Centro
Nacional de Metrología, se realizan
trabajos de caracterización a probadores
del tipo bidireccional y compacto con el
objetivo de conocer las influencias que
ocasionan en las mediciones las técnicas
y metodologías empleadas en estos tipos de probadores.
________* * * _______
En las siguientes líneas se da a conocer
los trabajos realizados y los resultados
de la comparación de las técnicas de
doble cronometría y cuádruple cronometría usadas en los probadores de volumen pequeño.
En las pruebas y en especifico para implementar la técnica de doble cronometría se utilizaron tres contadores de pulsos, dos de los cuales fueron usados
para la obtener la medición de tiempo
entre sensores y tiempo del numero de
pulsos enteros colectados en la pasada
de calibración, el tercer contador se utilizó para obtener el total de números
enteros correspondientes a cada pasada.
En la implementación de la cuádruple
cronometría, el proceso de conteo de
tiempos y pulsos se realizo mediante el
uso de una tarjeta contadora de National
Instruments. Las demás señales de temperatura y presión del medidor y probador fueron adquiridas por una tarjeta de
adquisición de datos del mismo fabricante.
En el proceso de pruebas se utilizo una
turbina del fabricante Brooks como
elemento de comparación, la cual se
instaló aguas arriba del probador, en
una línea con bombeo regulado por un
variador de velocidad, el cual proporciona un flujo constante de aproximadamente ± 0.3 %. Los flujos a los cuales
se realizaron las pruebas fueron los siguientes:
5 800, 5 000, 4 100, 3 400, 2 550 y 1
900 para los cuales se realizaron hasta
60 pasadas por flujo.
En la figura 4, se presenta un diagrama
esquemático de conexiones llevados a
cabo para las pruebas de doble y cuádruple cronometría.
Del probador
1.256 859 356 8
1.256 45 8 595 6
Circuito de sincronización y Control
388 _
tanto a la tarjeta de adquisición de pulsos como a los contadores de tiempo y
de pulsos de la técnica de doble cronometría, además de determinar y controlar la posición del pistón en el interior
del cilindro, mediante la detección del
paso de bandera en los sensores ópticos.
El programa de adquisición se realizo
en el CENAM, considerando para ello
que la resolución de los contadores de la
tarjeta, debería de ser a lo menos de
0,000 001 segundos (20 bits), quedando
una resolución de 0,000 000 10 (24 bits
y capacidad del oscilador), para cada
contador de tiempo, no siendo así para
el contador de pulsos el cual quedo con
una resolución de 65 536 de pulsos
máxima (16 bits).
Nat.Ins.
0. 002 859 268 9
0. 002 798 825 5
0. 000 593 457 1
0. 000 935 547 6
El equipo usado para estos trabajos se
detalla a continuación:
Probador Compacto (del tipo pistón).
388 _
Marca: EG&G
Serie: OF93120009
Figura 4. Diagrama de conexión
Esquemática de las técnicas de interpolación por doble cronometría y
cuádruple cronometría
En la instalación de la figura 4 cabe
mencionar que la problemática de diferencias de osciladores en el conteo
tiempo, y principalmente en la técnica
de doble cronometría, que son instrumentos independientes, se eliminó
usando un solo oscilador para los contadores mencionados (en la cuádruple
cronometría se usa el mismo oscilador
de la tarjeta).
En el circuito sincronizador de señales
se encarga de propiciar la misma señal
Modelo:
OF-1500102A
Vol.Cert.:
61, 154 8 L
Instrumento de comparación, medidor
tipo turbina.
Marca: Brooks instruments
Serie: xxxxxxx
Modelo:
xxxxxxx
Factor k:
xxxxxxxx
Rango de op: xxxxxx
Computadora portátil para cuádruple
cronometría.
Marca: MicroExpress
Serie:
Modelo:
Contadores universales de pulsos (para
tiempos t1 y t2).
Marca: Hewlett Packard
Oscilador:
Serie:
10 GHz
Modelo:
53131A
Indicador de temperatura del cilindro y
del soporte de los sensores.
Frecuencia:
225 MHz
Indicador de presión.
Resolución:
10 digitos
Oscilador:
5 GHz
NOTA: En el grueso de la calibración
se detecto un cambio en cada flujo de
aproximadamente 0,7% esto calculado
a partir de la determinación por la relación Volumen certificado del probador por el tiempo de sensor a sensor.
Contador universal de pulsos.
Marca:
Serie:
Modelo:
Frecuencia:
xxxx MHz
Resolución:
xxxx digitos
Oscilador:
xxxx GHz
Tarjeta contadora.
Marca: National Instruments
Modelo:
PCTIO-10
Frecuencia:
7 MHz
Flujo
5 915
4 996
4 154
3 407
2 546
1 897
En la tabla 1 se muestran los resultados
en cuanto a factor k del medidor, la
desviación estándar del factor y su por
ciento, esto de cada flujo de calibración
y para cada una de las dos técnicas de
interpolación de pulsos tratadas.
Factor k
Doble Cronometría
Cuádruple Cronometría
Promedio
Desv_estándar
% Desv_est.
Promedio
Desv_estándar
% Desv_est.
Promedio
Desv_estándar
% Desv_est.
Promedio
Desv_estándar
% Desv_est.
Promedio
Desv_estándar
% Desv_est.
Promedio
Desv_estándar
% Desv_est.
6,300 724
0,007 631
0,121%
6,297 948
0,007 819
0,124%
6,300 065
0,007 827
0,124%
6,309 061
0,007 446
0,118%
6,303 289
0,007 439
0,118%
6,300 596
0,007 979
0,127%
6,280 591
0,005 169
0,082%
6,288 720
0,003 932
0,063%
6,295 686
0,003 473
0,055%
6,296 783
0,002 220
0,035%
6,298 420
0,000 864
0,014%
6,295 485
0,001 186
0,019%
Tabla1. Datos de la calibración de una turbina utilizando las técnicas de doble
y cuádruple cronometría en la interpolación de pulsos.
uno de los flujos antes mencionados
además de su respectiva desviación estándar para cada punto mencionado.
En la figura 6, se presenta la gráfica
donde aparecen las líneas de tendencia
formadas por los puntos del factor k del
medidor turbina, encontrados para cada
Técnicas Doble y Cuádruple Cronometría
(desviación estándar)
6,320
6,315
6,310
Factor k (p/L)
6,305
6,300
6,295
6,290
6,285
6,280
6,275
6,270
1 600
2 100
2 600
3 100
3 600
4 100
4 600
5 100
5 600
6 100
Flujo (L/min)
Doble Cronometría
Cuádruple Cronometría
Figura 6. Gráfica de la desviación estándar en cada técnica y para cada uno de
los factores de la turbina en calibración.
Incertidumbre.
Existen dos métodos principales para
cuantificar las fuentes de incertidumbre
[1]: El Método de Evaluación Tipo A
está basado en un análisis estadístico de
una serie de mediciones, mientras el
Método de Evaluación Tipo B comprende todas las demás maneras de estimar la incertidumbre.
La diferencia en la evaluación de incertidumbre tipo A con respecto a la de
tipo B es que en la primera se estima
una distribución basándose en las mediciones obtenidas del mismo proceso de
medición, mientras que en el segundo
caso se supone una distribución con
base en experiencia de quien calibra o
información del instrumento.
Incertidumbre tipo A
A partir de la obtención de n datos del
factor k de la turbina, y con la dispersión de sus valores, establecemos de la
manera siguiente la incertidumbre de
tipo A del factor k:
UA =
Sq t
n
=
t
n
$Ú
HL
.
n
1
qi - q
.
n - 1 i=1
2
Donde:
UA:
Sq:
Incertidumbre de tipo A,
Desviación estándar de
los valores qi,
Numero de valores qi,
Distribución t de Student,
Valor i de el factor k.
n:
t:
qi:
De tal manera que al realizar este análisis para cada uno de los 6 flujos de calibración, y para cada una de las técnicas
tratadas, podremos obtener la contribución de incertidumbre tipo A por cada
una de ellas.
Incertidumbre tipo B
En las ecuaciónes 1-9, se define el modelo matemático a utilizar para esta calibración. De esta formulación se realizará un análisis de la contribución, que
tiene cada una de las variables que intervienen, a la incertidumbre del tipo B.
Fk =
Pulsos´
Volumen
Pulsos´ = N
t1
t2
1
“
Pulsos´ = N +
t1 t2
t3 t4
Volumen = V20 CTS1 CTS2 CPS CTL CPL
HL
HL
HL
HL
V20 = en certificado de probador
CTS1 = 1 + a1 Ts - 20
CTS2 = 1 + a2 Tp - 20
CPS =
Pp DI
Ep t
CTL = 1 + b Tm - Tp
CPL =
HL
H
L
HL
HL
HL
HL
HL
HL
HL
1
1 + F Pm - Pp
2
3
4
5
6
7
8
9
De una manera general definiremos la
incertidumbre del tipo B como la sumatoria de la incertidumbre de cada una de
las variables que aparecen en el modelo
matemático anterior. Su formulación es
la siguiente.
UB =
ik HL
y
&Ú
{
n
¶f
i=1 ¶
Xi
2
.U xi
Donde:
UB : Incertidumbre de tipo B,
¶ f
¶ Xi
: Coeficiente de sensitividad Xi
(variable i), en el modelo matemático f
U(Xi): Incertidumbre asociada a la
variable i,
Es conocido que, de la incertidumbre
total del factor k del medidor, la mayor
contribución a esta es la propia incertidumbre del probador usado, es también
sabido que cualquier técnica de redondeo o de interpolación de pulsos no es
suficiente para asegurar que el factor k
obtenido es totalmente fiable, ni la incertidumbre obtenida por este proceso
de calibración es la incertidumbre correspondiente, ya que en el proceso de
calibración se toma una muestra muy
pequeña de los pulsos del medidor, cuyo comportamiento es generalmente
irregular lo cual ocasiona que al estimar
el numero de pulsos por unidad de volumen no sea del todo aplicable a cualquier pulso emitido por el medidor,
aunque a este respecto la norma ISO [3]
sugiere un numero n datos a recolectar
por muestra, donde n tiene correspondencia a la desviación estándar porcentual de la forma de los pulsos del medidor (periodo).
En la tabla 2 se muestran los resultados
de incertidumbre tipo A y tipo B, de las
técnicas tratadas, en la tabla se puede
observar la contribución de cada una de
estas a la incertidumbre total del factor
k del medidor.
Flujo
Υ factor k
Υ Total
% Υ Total
Cronometría
t Student
ΥA
ΥB
Doble
Cuádruple
Doble
Cuádruple
Doble
Cuádruple
Doble
Cuádruple
Doble
Cuádruple
Doble
Cuádruple
2,13
2,11
2,11
2,09
2,11
2,11
2,06
2,06
2,13
2,13
2,13
2,13
0,003 764
0,002 414
0,004 836
0,002 002
0,003 655
0,001 585
0,003 477
0,001 062
0,003 560
0,000 377
0,003 640
0,000 529
0,000 977
0,000 974
0,000 975
0,000 975
0,000 977
0,000 976
0,000 979
0,001 017
0,000 978
0,000 976
0,000 977
0,000 976
5 915
4 996
4 154
3 407
2 546
1 897
0,003 889
0,002 603
0,004 934
0,002 227
0,003 784
0,001 861
0,003 612
0,001 470
0,003 692
0,001 047
0,003 769
0,001 110
0,123%
0,083%
0,157%
0,071%
0,120%
0,059%
0,115%
0,047%
0,117%
0,033%
0,120%
0,035%
Tabla2. Resultados de la contribución de la incertidumbre tipo A y B en la incertidumbre total del Factor k del medidor en calibración.
Conclusión.
vamente reducida (y en gran medida
debido a la incertidumbre de tipo A).
Aunque es conocido que la contribución
a la incertidumbre total, por cualquiera
de las técnicas mostradas, es me mucho
menor que la incertidumbre se sabe es
atribuida a los pulsos debido a su irregularidad, no se puede ignorar que la
incertidumbre por el uso de la técnica
de cuádruple cronometría es comparati-
En la tabla 3 se muestran las conclusiones en forma de tabla de resultados de la
diferencia de las dos técnicas. En Principio se muestra la diferencia que existe
entre los resultados del factor k y en
segundo lugar la diferencia en el resultado de incertidumbre para cada técnica.
Flujo
(L/min)
5 915
4 996
4 154
3 407
2 546
1 897
Desviación factor k
ΥTotal factor k (p/L)
(p/L)
%
Doble C.
Cuádruple C.
0,020 1
0,009 2
0,004 4
0,012 3
0,004 9
0,005 1
0,32
0,15
0,07
0,19
0,08
0,08
0,007 8
0,009 9
0,007 6
0,007 2
0,007 4
0,007 5
0,005 2
0,004 5
0,003 7
0,002 9
0,002 1
0,002 2
Diferencia
Υ factor k
(p/L)
0,002 6
0,005 4
0,003 8
0,004 3
0,005 3
0,005 3
Tabla3. Diferencias de incertidumbre de los datos del factor k obtenidos por la
comparación de las técnicas de doble y cuádruple cronometría en la interpolación de pulsos.
La desviación que se indica del factor k
en la tabla 3 es considerable y en algunos casos, mayor a la propia incertidumbre de la técnica empleada, comparativamente se observa que es mejor
contar con una técnica de cuatro contadores para la interpolación de pulsos.
Bibliografía
[1] Guía para estimar la incertidumbre de la medición.
Wolfgang A. Schmid y Ruben J. Lazos Martínez
[2] Comprobadores de gasto en tuberías
Hayward
[3] ISO 7278-3. Liquid hydrocarbons – dynamic measurement – proving systems for volumetric meters – part 3:
pulse interpolation techniques.
International standards organization, ginebra.
[4] API
Manual of Petroleum Measurement Standards
Proving System. Chapter 4.6. Pulse interpolation.
[5] Proceedings of the Seventy-sixth International School of
Hydrocarbon Measurement 2001