Solución
Anuncio

T3: TRIGONOMETRÍA
1º BCT
ÁREA DE UN ROMBO
Dado un rombo cuyo lado mide 36 cm y uno de sus ángulos mide 38º 20´, calcula:
a) La medida de sus diagonales.
b) Su área.
Solución
B
B
36 cm
Extrayendo el triángulo AOB
38º 20´
A
36 cm
C
19º 10´
O
A
D
a) Calculamos las dos diagonales:
Diagonal BD:
sen A =
OB
→ OB = AB·sen A → OB = 36 · sen 19º 10´ = 11,82 cm
AB
BD = 2 · OB = 2 · 11,82 = 23,64 cm
Diagonal AC:
cos A =
OA
→ OA = AB·cos A → OA = 36 · cos 19º 10´ = 34 cm
AB
BD = 2 · OA = 2 · 34 = 68 cm
b) Área del rombo =
BD· AC
23,64·68
2
=
= 803,76 cm
2
2
También se puede calcular:
Área del rombo = 4 · área triángulo AOB = 4·
11,82·34
2
= 803,76 cm
2
TORRE DE TELEVISIÓN.
Ana y Pedro ven desde la puerta de sus casas una torre de televisión, bajo ángulos de 45º y 60º,
respectivamente. La distancia entre la casa de Pedro y la torre es de 75 m. Si la entena está situada
entre sus casas, halla la altura de la torre y la distancia de la misma a la casa de Ana.
Solución
En el triángulo DBC:
tg60º =
B
h
→ h = 75· tg 60º = 75·1,73 = 129,75
75
h
La altura es 129,75 m
En el triángulo DBC:
h
tg 45º = → h = y = 129,75 →
y
45º
A
60º
x
D
C
75
La distancia a casa de Ana es 129,75 m
Luisa Muñoz
2
T3: TRIGONOMETRÍA
1º BCT
EL CAMPO DE FÚTBOL.
Un campo de fútbol mide 40 m de ancho y la portería tiene 8 m de ancho. Si un jugador está situado en
la banda lateral, a 12 m de la línea de fondo, ¿bajo qué ángulo ve la portería?
8m
12 m
40 m
Solución
El problema nos pide calcular el ángulo α.
C
α
Empleando el triángulo ACD, tenemos:
12 m
CD 12 1
tg A =
=
=
→ A = 26º 33´ 54´´
AD 24 2
Empleando el triángulo BCD, tenemos:
tg B =
B
A
8m
16 m
D
CD 12 3
=
=
→ B = 36º 52´ 12´´
BD 16 4
El ángulo ABC = 180º − B = 180º – 36º 52´ 12´´ = 143º 7´ 48´´
El ángulo α mide: 180º – (143º 7´ 48´´ + 26º 33´ 54´´) = 180º – 169º 41´42´´ = 10º 18´18´´
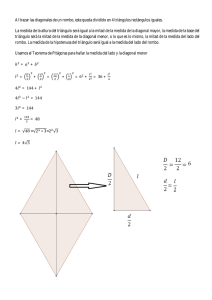
ALTURA CORRESPONDIENTE A LA HIPOTENUSA
Los catetos de un triángulo rectángulo son 3 y 4 m. Hallar la altura correspondiente a la hipotenusa.
Solución
Calculamos la hipotenusa, aplicando el teorema de Pitágoras:
A
CB = 5 ({3, 4, 5} terna pitagórica)
4
C
3
h
Empleando el triángulo ABC:
α
D
B
sen α =
4
5
Empleando el triángulo ADB:
sen α =
h
4 12
→ h = 3·sen α = 3· =
3
5
5
La altura es 2,4 cm
Luisa Muñoz
3
T3: TRIGONOMETRÍA
1º BCT
ÁREA DE UN HEXÁGONO
Calcular el área de un hexágono regular de 5cm de lado.
Solución:
Cálculo de la apotema:
sen 60º =
h
→ h = 5 · sen 60º = 4,33 → a = 4,33 cm
5
Cálculo del área:
5
h
60º
A=
p · a 6 · 5 · 4,33 129,9
2
=
=
= 64,95 → Área = 64,95 cm
2
2
2
LA ANTENA
Tenemos una antena sujeta por dos cables anclados en los puntos C y D.
Si el anclaje C se encuentra a 50 m del pie de la antena, calcular:
a) Altura de la antena (AB)
A
b) Distancia entre los dos anclajes (CD)
30º
Nota: CBD = 90º
45º
100 m
B
D
C
Solución:
a) tg 30º =
CB
CB
100
→ AB =
=
= 173,3 → AB = 173,3 m
AB
tg 30º tg 30º
b) BD = AB por ser isósceles (dos ángulos iguales)
CD = CB + BD → CD = 100 + 173,3 → CD = 200,08 m
2
2
Luisa Muñoz
2
2
2
2
4