VIII – Política monetaria y fiscal

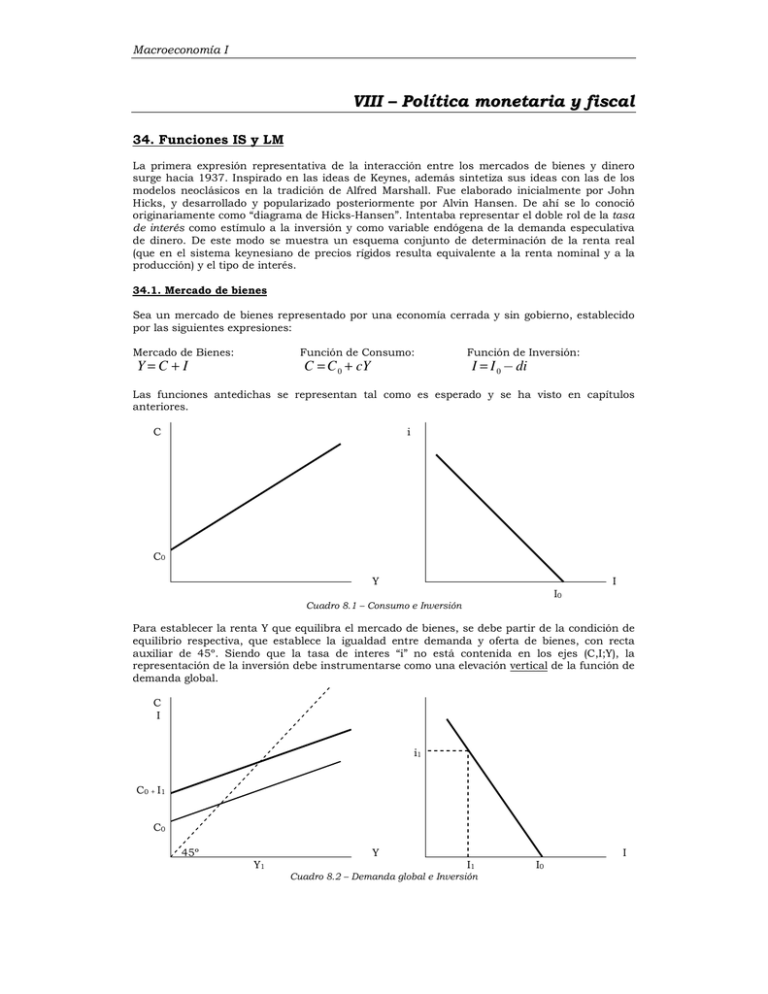
Macroeconomía I
VIII – Política monetaria y fiscal
34. Funciones IS y LM
La primera expresión representativa de la interacción entre los mercados de bienes y dinero
surge hacia 1937. Inspirado en las ideas de Keynes, además sintetiza sus ideas con las de los
modelos neoclásicos en la tradición de Alfred Marshall. Fue elaborado inicialmente por John
Hicks, y desarrollado y popularizado posteriormente por Alvin Hansen. De ahí se lo conoció
originariamente como “diagrama de Hicks-Hansen”. Intentaba representar el doble rol de la tasa
de interés como estímulo a la inversión y como variable endógena de la demanda especulativa
de dinero. De este modo se muestra un esquema conjunto de determinación de la renta real
(que en el sistema keynesiano de precios rígidos resulta equivalente a la renta nominal y a la
producción) y el tipo de interés.
34.1. Mercado de bienes
Sea un mercado de bienes representado por una economía cerrada y sin gobierno, establecido
por las siguientes expresiones:
Mercado de Bienes:
Función de Consumo:
C = C 0 + cY
Y=C + I
Función de Inversión:
I = I 0 @ di
Las funciones antedichas se representan tal como es esperado y se ha visto en capítulos
anteriores.
C
i
C0
Y
I
I0
Cuadro 8.1 – Consumo e Inversión
Para establecer la renta Y que equilibra el mercado de bienes, se debe partir de la condición de
equilibrio respectiva, que establece la igualdad entre demanda y oferta de bienes, con recta
auxiliar de 45º. Siendo que la tasa de interes “i” no está contenida en los ejes (C,I;Y), la
representación de la inversión debe instrumentarse como una elevación vertical de la función de
demanda global.
C
I
i1
C0 + I1
C0
45º
Y
Y1
I
I1
Cuadro 8.2 – Demanda global e Inversión
I0
23
Macroeconomía I
Precisamente por esta razón, los cambios en valores de la tasa de interés reflejarán
desplazamientos en la función de demanda global; así, si en el gráfico anterior, la tasa de
interés descendiera a i2, la inversión aumentaría a I2, y con ella la demanda global.
Nótese que el aumento de la inversión de I1 a I2 ha provocado un aumento en el ingreso de Y1 a
Y2, el que es mayor al aumento de la inversión original, por la existencia del efecto
multiplicador, 1/(1-c).
C
I
b
a
i1
C0 + I2
C0 + I1
i2
C0
45º
Y
Y1
I
Y2
I1
I2
I0
Cuadro 8.3 – Desplazamiento de la demanda global
Esto indica que ante la disminución de la tasa de interés, el nivel de ingreso que equilibra la
demanda y oferta de bienes aumenta, puede reflejarse en la siguiente expresión:
Y = C 0 + cY + I 0 @ di
`
a
Y 1 @ c = C 0 + I 0 @ di
+
If
Cf
df
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f f
f
f
f
f
f
f
f
f
f
f
f
f
f
Y= 0 0 @
i
1@c 1@c
i
-d/(1-c)
i1
a
i2
b
C0
IS
Y
Y1
Y2
(C0+I0)/(1-c)
I
I1
I2
I0
Cuadro 8.4 – Función IS
Esta función en el espacio (i;Y) se denomina función “IS”, debiendo su nombre a la igualación de
Inversión (investment) y Ahorro (savings). La pendiente negativa se explica por el hecho de que
una disminución en la tasa de interés estimulará un aumento en la inversión, y éste a su vez
generará un aumento en el producto y consumo (vía multiplicador).
La antedicha es la expresión del equilibrio en el mercado de bienes. Es la expresión de una recta
con abscisa al origen
Cf
+
If
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
0f
0f
y
1@c
pendiente
df
f
f
f
f
f
f
f
f
f
f
f
f
f
f
, tal
1@c
como se ha mostrado en el gráfico
precedente.
Podemos reexpresar los elementos autónomos y el multiplicador como:
23
Macroeconomía I
1f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
C0 + I 0 = A
1@c
Por tanto, es:
`
=α
a
Y = Aα @ dαi = α A @ di
Alternativamente, podemos despejar en la expresión antedicha la tasa de interés:
Y = C 0 + cY + I 0 @ di
di = C 0 + cY @ Y + I 0
+
If
Cf
@
cf
1f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f 1f
f
f
f
f
f
f
f
f
f
f
f
f A
f
f
f
f f
f
f
f
f
f
f
0f
0f
i= f
@ f
= f
@ f
Y
d
d
d αd
De esta forma se consigue una expresión que muestra la tasa de interés en términos de la renta,
y es análoga a la anterior. Si bien presenta menos lógica económica, nos muestra el valor de la
ordenada al origen de la expresión IS:
A/d
i
i1
a
i2
b
C0
IS
Y
Y1
Y2
Aα
Cuadro 8.5 – Ordenadas y abscisas de la función IS
Resulta sencillo en el gráfico anterior identificar los puntos resultantes con sus homólogos en
un gráfico de demanda global:
A/d
C
I
G
I
C+I(i2)
b
d
C+I(i1)
i1
a
c
c
a
C0
i2
d
b
IS
Y
Y1
Y2
Aα
Y
Cuadro 8.6 – Puntos de la función IS y de la demanda global
34.2. Mercado de Dinero
Se caracteriza el mercado monetario como de oferta monetaria rígida, debida a la inexistencia de
un sistema bancario. Su expresión es:
s
M =M0
23
Macroeconomía I
i
M0
M
Cuadro 8.7 – Oferta Monetaria
La demanda monetaria recoge los antecedentes keynesianos basados en los motivos para
mantener el dinero, denominados como transacción y precaución, y especulación. Los dos
primeros se entienden vinculados directamente a la renta, y el tercero se reconoce como
vinculado inversamente al tipo de interés, como se ha visto en el capítulo correspondiente al
mercado de dinero:
Demanda de Dinero:
d
Demanda para Transacciones:
Demanda Especulativa:
Lt = kY
M = Lt + Le
Le = L0 @ hi
El equilibrio en el mercado de dinero puede establecerse siguiendo premisas análogas a las
establecidas anteriormente para el mercado de bienes. Se descuenta que la variable exógena
que puede implicar cambios en este mercado es la renta (Y), así como en el mercado de bienes lo
era la tasa de interés.
Lt
i
kY
Y
Le
Cuadro 8.8 – Demanda para transacciones y para especulación
En los dos gráficos precedentes se muestra la demanda para transacciones, Lt, y la demanda
especulativa, Le.
Lt
i
i1
Lt1
Y
Y1
Le
Le1
L0
Le+Lt
Cuadro 8.9 – Demanda total de dinero
Puede observarse en el diagrama de la derecha que si el nivel de ingreso ascendiese a Y2,
quedaría como sigue:
23
Macroeconomía I
Lt
i
Lt2
i2
d
Lt1
i1
c
Y
Y1
Y2
L0 M0 Le+Lt1 Le+Lt2
Cuadro 8.10 – Demanda y oferta monetaria
El desplazamiento horizontal se debe a que la modificación en la renta real (Y), no contenida en
los ejes, implica un aumento en la demanda total de dinero que no puede ser reflejado por la
función previa. En consecuencia, ante los aumentos en el nivel de renta se produce un aumento
en la tasa de interés, como se muestra a continuación:
i
LM
i2
d
i1
d
c
c
Y
Y1
Y2
M0 Le+Lt1 Le+Lt2
(L0-M0)/h
Cuadro 8.11 – Mercado monetario y función LM
Nótese que la ordenada al origen de la expresión es negativa. Esto se debe al hecho de que la
suma total de fondos especulativos L0 no podría ser superior a la oferta total de dinero M0.
La derivación de la relación LM puede asimismo formularse algebraicamente:
M 0 = kY + L0 @ hi
hi = kY + L0 @ M 0
Lf
@
M
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f kf
f
f
0f
0f
i= f
+ f
Y
h
h
La antedicha es la expresión del equilibrio en el mercado de dinero despejando el tipo de interés.
Esta determinación es apta para la solución del sistema de ecuaciones que implica la
integración con el mercado de bienes aplicando el método de sustitución, como se verá más
adelante. La expresión obtenida muestra el valor del tipo de interés que equilibra oferta y
demanda de dinero. El término de la izquierda muestra la ordenada al origen y el de la derecha
(k/h) evidencia la pendiente de la expresión LM. Esta expresión debe su nombre a la sigla que
combina la liquidity preference (demanda monetaria) y money (oferta monetaria).
Alternativamente, puede despejarse el nivel de renta en este mercado:
M 0 = kY + L0 @ hi
hi @ L0 + M 0 = kY
Mf
@
Lf
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f hf
f
f
0f
0f
Y= f
+ f
i
k
k
Esta condición alternativa del equilibrio del mercado de dinero muestra la abscisa al origen de
la expresión y su pendiente, aunque en forma invertida:
23
Macroeconomía I
i
i2
d
i1
c
(M0-L0)/k
Y
Y1
Y2
(L0-M0)/h
Cuadro 8.12 – Ordenadas y abscisas de la función LM
Al igual que con el modelo IS, resulta sencillo identificar puntos homólogos en un gráfico LM y
en un gráfico que representa demanda y oferta monetaria.
i
i
M0
L(Y1) L(Y2)
i2
i1
e
d
i2
c
f
i1
e
d
c
f
Y
Y1
L,M
(L0-M0)/h
Y2
Cuadro 8.13 – Puntos de la función LM y del mercado monetario
35. Propiedades del modelo IS-LM
35.1 Función IS. Propiedades
Se presenta a continuación un gráfico IS en el cual pueden mostrarse las ordenadas y abscisas
al origen:
i
A/d
-d/(1-c)
A/(1-c)
Y
Cuadro 8.14 – Función IS, pendientes y puntos de corte
Puede apreciarse que la posición de la función IS está determinada en forma directa por los
elementos autónomos, y por el multiplicador, y en forma inversa por un aumento en la
propensión a invertir.
23
Macroeconomía I
A’/d
A’>A
A/d
c’>c
d’>d;
A/d
A/d’
A/(1-c)
A’(1-c)
A/(1-c)
A/(1-c’)
Y
Y
Y
Cuadro 8.15 – Desplazamientos de la función IS
Se prueba que la pendiente de la función de inversión (“d”) determina la pendiente de la IS:
C+I
I
45º
DG2
b
DG1
a
C+I2
DG0
e
C+I1
C+I0
Y
i
I
i
e
i0
e
a
b
a b
i1
IS’
0
Y0
Y1
Y2
IS
I’
0
I0
I1
I
I2
Cuadro 8.16 – Demostración de la pendiente de la función IS
Y cambios en “c” y “d” modifican las abscisas u ordenadas al origen, y simultáneamente
modifican la pendiente de IS.
i
i
i
i
Y
Aumento en el gasto
autónomo C0 ó I0
Y
Aumento en “d”
(reacción de la inversión)
Y
Y
Aumento en PMgC (“c”) Disminución en PMgC
ó en el multiplicador
(“c”) o en multiplicador
Cuadro 8.17 – Resumen de movimientos comparativos de la función IS
23
Macroeconomía I
35.2 Función LM. Propiedades
Se muestra a continuación un gráfico de la función LM que exhibe ordenada y abscisa al origen:
i
k/h
(M0-L0)/k
Y
(L0-M0)/h
Cuadro 8.18 – Función LM
El siguiente gráfico muestra cómo un diferente valor de “k” (pendiente de la demanda para
transacciones) determina un diferente valor de pendiente de la función LM:
Lt
k3Y
L
k2Y
k1 Y
Lt3
Lt2
Lt1
b
a
e
Y
i3
L
b
i
a
i2
e
i1
0
Y0
e
Y1
0
M0
a b
L1 L2
L3
Cuadro 8.19 – Demostración de la pendiente de la función LM
Se puede mostrar que cambios en la oferta monetaria determinan cambios en la posición de la
función LM, así como que cambios en “k” y “h” determinan cambios en la pendiente de la
función, con algunas particuaridades:
23
Macroeconomía I
i
i
i
Y
Aumento en la oferta
monetaria (M0)
i
Y
Aumento en “k”
Y
Aumento en L0
Y
Aumento en “h”
(modificación en cruz)
Cuadro 8.20 – Resumen de movimientos comparativos de la función LM
36. Desequilibrios en IS y LM
Se puede demostrar la existencia de un único par de valores (i; Y) que satisface
simultáneamente los equilibrios del mercado de bienes y del mercado de dinero. Esta
demostración puede fundarse en principios geométricos, como también algebraicamente.
36.1 Desequilibrios en el mercado de bienes
Veamos en principio el mercado de bienes, representado por la función IS. En el gráfico que se
muestra a continuación debe quedar en claro que a lo largo de todos los puntos de la función IS
el mercado de bienes se encuentra equilibrado. Esto significa que la oferta y la demanda de
bienes se hallan igualadas.
i
ΕΟΒ
A/d
EDB
IS
Y
Aα
Cuadro 8.21 – Desequilibrios en el mercado de bienes
Queda evidenciado en el gráfico precedente que cualquier punto que se halle a la izquierda o por
debajo de la función IS representa un exceso de demanda de bienes, dado que deberá aumentar
la producción (oferta), para que así alcance al valor de la mayor demanda, o bien aumentar la
tasa de interés, para así deprimir la inversión, que es un componente de la demanda, y así
adecuarla a la menor oferta. Claro está que podrá ocurrir una combinación de ambos ajustes.
En sentido contrario, cualquier punto que se halle a la derecha o por encima de la función IS,
representa un exceso de oferta de bienes, dado que deberá disminuir la producción (oferta) para
adecuarla a la menor demanda, o bien disminuir el tipo de interés para estimular la inversión
(demanda), para así alcanzar la mayor oferta. Asimismo podrá aquí ocurrir una combinación de
ambos ajustes.
36.2 Desequilibrios en el mercado de dinero
Veamos ahora el mercado de dinero, representado por la función LM. En el gráfico que se
muestra a continuación se aprecia que a lo largo de todos los puntos de la función LM el
mercado de dinero se encuentra equilibrado. Esto significa que la oferta y la demanda de dinero
se hallan igualadas.
23
Macroeconomía I
i
LM
EOM
EDM
(M0-L0)/k
Y
(L0-M0)/h
Cuadro 8.22 – Desequilibrios en el mercado de dinero
Se muestra en el gráfico precedente que cualquier punto que se halle a la izquierda o por
encima de la función LM representa un exceso de oferta de dinero, dado que deberá aumentar el
ingreso, para que así aumente la demanda para transacciones y así alcance al valor de la mayor
oferta, o bien disminuir la tasa de interés, para así estimular la demanda especulativa de dinero
y asi alcanzar la mayor oferta. Una vez más, podrá ocurrir una combinación de ambos ajustes.
En sentido contrario, cualquier punto que se halle a la derecha o por debajo de la función LM,
representa un exceso de demanda de dinero, dado que o bien deberá disminuir el ingreso para
así restringir la demanda de dinero para transacciones, o bien aumentar el tipo de interés para
restringir la demanda especulativa, y en cualquiera de ambos casos adecuarla a la restricción
de oferta. Podrá ocurrir aquí también una combinación de ambos ajustes.
36.3 Equilibrio simultáneo de ambos mercados
Una superposición de los gráficos que representan las tensiones dinámicas en ambos mercados
se presenta a continuación:
i
LM
IS
Y
Cuadro 8.23 – Tensiones dinámicas en IS-LM
Puede apreciarse que existen fuerzas contrapuestas. El interrogante es cuales de ellas
triunfarán, y ver si de la combinación de esas fuerzas puede derivarse que el sistema será o no
estable.
El principio de correspondencia de Samuelson, que genéricamente puede resumirse
simplificadamente en la sentencia “el exceso de demanda u oferta en un mercado afectará
preferentemente al precio o variable de equilibrio de ese mercado” nos acerca a la respuesta.
Implica que los excesos de demanda y oferta en el mercado de bienes afectarán preferentemente
(y más inmediatamente) a la variable representativa de ese mercado, que aquí es la producción
u oferta (Y); y análogamente, los excesos de demanda u oferta en el mercado monetario
afectarán preferentemente a la tasa de interés (i).
Suponer lo contrario (que los desequilibrios en el mercado de bienes afectarán
preeminentemente al tipo de interés y que los desequilibrios en el mercado de dinero afectarán
preeminentemente a la producción) es, además de contrario al sentido común, una violación al
principio de correspondencia enunciado, que puede ser demostrado matemáticamente.
De ese modo podemos depurar las flechas antedichas, de modo tal que:
23
Macroeconomía I
a) en caso de discrepancia respecto de cuál de las fuerzas contrapuestas triunfará respecto del
producto (cuadrantes II y IV), deberemos privilegiar aquellas vinculadas con el mercado de
bienes.
b) en caso de discrepancia respecto de cuál de las fuerzas contrapuestas triunfará respecto de la
tasa de interés (cuadrantes I y III), deberemos privilegiar aquellas vinculadas con el mercado de
dinero.
El gráfico resultante de esta depuración de flechas dinámicas es el siguiente:
i
II
III
LM
I
IV
IS
Y
Cuadro 8.24 – Tensiones dinámicas resultantes en IS-LM
Se comprueba así la tendencia natural de giro en sentido contrario a las agujas del reloj para el
caso de ajuste dinámico a cualquier desequilibrio, y asimismo la estabilidad del modelo, en el
sentido de que, ante cualquier perturbación, el sistema volverá automáticamente a su punto de
equiibrio.
37. Estática comparativa en IS-LM
Se considera estática comparativa a la comparación entre dos situaciones de equilibrio, a una
de las cuales se le ha aplicado o introducido algún tipo de perturbación. En el modelo IS-LM, la
fuente esencial de perturbaciones con impacto estático-comparativo surge de las modificaciones
que el Estado puede introducir en el mercado de bienes (lo que afectaría la posición de la
función IS), o en el mercado de dinero (lo que afectaría la posición de la función LM).
Suele llamarse al primer grupo de perturbaciones política fiscal, y al segundo grupo de
perturbaciones política monetaria.
Deberá asimismo tenerse en cuenta el sentido de ambas políticas, medido en su impacto
esperado sobre la renta. Así, las políticas fiscales o monetarias expansivas serán aquellas que
pretenden aumentar la renta, y contractivas aquellas que pretenden disminuirla, dicho esto con
prescindencia del análisis del posible éxito o fracaso de tales intentos.
37.1. Política fiscal expansiva: aumento del gasto público
Se considera política fiscal expansiva a un aumento en el déficit fiscal, o a una disminución en
el superávit fiscal. Este puede ser obtenido mediante un aumento liso y llano en el gasto
público, o una disminución en los impuestos. En este caso consideraremos una expansión fiscal
debida a un aumento en la demanda de bienes por parte del gobierno (gasto público). Cabe
considerar que la disminución en los impuestos tiene idéntico efecto, pero si éstos son
proporcionales a la renta, puede afectar la pendiente de la demanda global, y como se ha visto,
con ella, la pendiente de la función IS, caso que se verá más adelante.
Partimos de un equilibrio original IS, materializado en el mercado de bienes como el equilibrio
de la demanda global DG1 en su intersección con la línea auxiliar de 45 grados (sucedáneo de la
oferta de bienes), en el punto “a”, y un equilibrio original LM materializado en el mercado de
dinero como la intersección entre la oferta monetaria M0 y la demanda monetaria L, en el punto
“a”. Ambos equilibrios se expresan en el gráfico IS-LM en un punto designado asimismo con la
letra “a”.
23
Macroeconomía I
C
I
G
DG2
DG3
DG1
b
c
a
Y
i
i
LM
c
i2
c
a
i1
a
M0
b
b
L
L’
IS
Y
Y1 Y2 Y3
IS’
∆Gα Y
Cuadro 8.25 – Expansión fiscal en IS-LM
Una expansión fiscal originada, por ejemplo, en un incremento en las compras de bienes y
servicios por parte del gobierno, provocará un desplazamiento de la función de demanda global
de DG1 a DG2, y un consecuente incremento inicial de la renta de equilibrio de Y1 a Y3 tal como
se muestra en el punto “b”. El aumento de la renta de Y1 a Y3 equivale al incremento en el gasto,
amplificado por el multiplicador keynesiano convencional.
Este pasaje de “a” a “b” se puede ver en el gráfico IS-LM como un desplazamiento horizontal y
en paralelo de IS a IS’, donde a igual tasa de interés, i1, la renta ha experimentado un aumento
de Y1 a Y3.
Es en este punto donde el mercado de bienes se halla en equilibrio, pero no lo hay en el
mercado monetario, el que presenta un desequilibrio caracterizado por un exceso de demanda
de dinero (dado que el punto “b” se halla a la derecha y por debajo de la función LM original).
Las razones del mismo radican en que, al haber aumentado la renta de equilibrio, la demanda
monetaria para transacciones se incrementó en un valor equivalente al coeficiente “k”
multiplicado por tal incremento de renta, de L a L’. Este punto se exhibe como “b” en el gráfico
del mercado de dinero (a la izquierda del gráfico IS-LM). Y muestra asimismo el exceso de
demanda que, a la tasa de interés i1 existe por sobre la oferta monetaria M0.
Este exceso presionará al alza la tasa de interés en el mercado monetario, hasta encontrar su
equilibrio en el valor i2, generando un equilibrio en el mercado de dinero caracterizado por el
punto “c”. Pero este aumento en la tasa de interés es una señal que inducirá a los inversores
privados a desistir o reducir sus proyectos de inversión, empujando hacia abajo la demanda
global, la que ahora se situará en DG3. El consecuente valor de la renta de equilibrio será Y2,
Macroeconomía I
23
consistente con el punto “c”. Este punto se correlaciona con su homónimo en el gráfico IS-LM.
Así, el par de valores (Y2, i2) será el nuevo equilibrio de ambos mercados, que se caracteriza por
reflejar un aumento parcial en la renta de equilibrio y un aumento parcial en el tipo de interés
de equilibrio.
Una consecuencia importante de esta política es que la inversión privada se contrajo
parcialmente, cediendo terreno a la inversión pública. Ha cambiado la composición del gasto, y
este efecto se conoce comúnmente como efecto desplazamiento (“crowding out”).
Se puede comprobar además que la efectividad de la política será mayor cuanto menor
pendiente tenga la función LM; esto es, que los valores finales se acerquen más a la solución
keynesiana tradicional (Y3), con escaso incremento en la tasa de interés por sobre i1. Por el
contrario, la política fracasará si el tipo de interés aumenta demasiado y la renta no lo hace, lo
que sería consecuencia de una función LM excesivamente empinada. Se muestra como ejemplo
extremo de esta situación el punto “d” en el cuadro IS-LM.
37.2. Política fiscal contractiva: aumento en la tasa impositiva
Consideraremos una contracción fiscal (un aumento en el superávit fiscal o disminución en el
déficit fiscal) originada en un aumento en la tasa impositiva, definida como una tasa
proporcional sobre los ingresos. Este cambio fiscal originará modificaciones en la pendiente de
la demanda global, debido a la reducción de la propensión marginal a consumir.
Partimos de un equilibrio original IS, materializado en el mercado de bienes como el equilibrio
de la demanda global DG1 en su intersección con la línea auxiliar de 45 grados (sucedáneo de la
oferta de bienes), en el punto “a”, y un equilibrio original LM materializado en el mercado de
dinero como la intersección entre la oferta monetaria M0 y la demanda monetaria L, en el punto
“a”. Ambos equilibrios se expresan en el gráfico IS-LM en un punto designado asimismo con la
letra “a”. La renta de equilibrio original es Y1 y la tasa de interés original de equilibrio es i1.
Una contracción fiscal originada, por ejemplo, en un incremento en la tasa impositiva sobre los
ingresos, provocará una disminución en la función de demanda global de DG1 a DG2, originada
en el cambio de pendiente de la misma por aplicación de la mayor tasa fiscal; y una
consecuente reducción inicial de la renta de equilibrio de Y1 a Y2 tal como se muestra en el
punto “b”.
Este pasaje de “a” a “b” se puede ver en el gráfico IS-LM como un desplazamiento de la función
IS a IS’ (la que no conserva su pendiente original, debido a que la reducción en la PMgC debida
a los impuestos afecta la pendiente de IS haciéndola más empinada, como se viera más arriba);
en este caso, a igual tasa de interés, i1, la renta ha experimentado una reducción de Y1 a Y2.
Es en este punto donde el mercado de bienes se halla en equilibrio, pero no lo hay en el
mercado monetario, el que presenta un desequilibrio caracterizado por un exceso de oferta de
dinero (dado que el punto “b” se halla a la izquierda y por encima de la función LM original). Las
razones del mismo radican en que, al haber disminuido la renta de equilibrio, la demanda
monetaria para transacciones disminuyó en un valor equivalente al coeficiente “k” multiplicado
por tal descenso en la renta, de L a L’. Este punto se exhibe como “b” en el gráfico del mercado
de dinero (a la izquierda del gráfico IS-LM), que muestra el exceso de oferta M0 que, a la tasa de
interés i1 existe por sobre la demanda monetaria L’.
Este exceso presionará a la baja la tasa de interés en el mercado monetario, hasta encontrar su
equilibrio en el valor i3, generando un equilibrio en el mercado de dinero caracterizado por el
punto “c”. Pero esta baja en la tasa de interés estimulará a los inversores privados a adquirir
bienes de inversión, empujando hacia arriba la demanda global, la que ahora se situará en DG3.
Nótese que este aumento es paralelo, a diferencia del anterior. El consecuente valor de la renta
de equilibrio será Y3, consistente con el punto “c”. Este punto se correlaciona con su homónimo
en el gráfico IS-LM. Así, el par de valores (Y3, i3) será el nuevo equilibrio de ambos mercados,
que se caracteriza por reflejar una disminución parcial en la renta de equilibrio y una
disminución parcial en el tipo de interés de equilibrio.
Se verifica aquí, a la inversa del caso anterior, un cambio en la composición del gasto total a
favor de los inversores privados y el consumo privado, y en detrimento del gasto gubernamental.
23
Macroeconomía I
C
I
G
DG1
a
DG3
DG2
c
b
Y
i
i1
LM
M0
b
a
b
a
i3
c
c
d
L
IS’
IS
L’
L
Y
Y2 Y3
Y1
Cuadro 8.26 – Aumento en la tasa impositiva en IS-LM
Se puede comprobar que el descenso en la renta será mayor cuanto más aplanada sea la
función LM; esto es, que los valores finales se acerquen más a la solución keynesiana
tradicional (Y2), con escaso descenso en la tasa de interés por sobre i1. Por el contrario, la
política logrará una reducción exigua en la renta si el tipo de interés disminuye demasiado y la
renta no lo hace, lo que sería consecuencia de una función LM excesivamente empinada. Se
muestra como ejemplo extremo el punto “d” en el cuadro IS-LM.
37.3. Política monetaria expansiva: emisión monetaria
Consideraremos una expansión monetaria, originada en un aumento en la oferta de dinero,
definida como una emisión de billetes y monedas que se lanzan a la circulación. Este objetivo
también podría ser alcanzado por cualquiera de las herramientas que generan un aumento en
la base monetaria. Este cambio originará modificaciones en la tasa de interés, la que se espera
tenga consecuencias en la demanda de bienes.
Partimos de un equilibrio original IS, materializado en el mercado de bienes como el equilibrio
de la demanda global DG1 en su intersección con la línea auxiliar de 45 grados (sucedáneo de la
oferta de bienes), en el punto “a”, y un equilibrio original LM materializado en el mercado de
dinero como la intersección entre la oferta monetaria M0 y la demanda monetaria L, en el punto
“a”. Ambos equilibrios se expresan en el gráfico IS-LM en un punto designado asimismo con la
letra “a”. La renta de equilibrio original es Y1 y la tasa de interés original de equilibrio es i1.
Una expansión monetaria originada, por ejemplo, en un incremento en la base monetaria por
impresión de billetes puestos en circulación, provocará un aumento en la oferta monetaria de
M0 a M1, la que enfrentada a una demanda monetaria L, provocará un abrupto descenso en el
tipo de interés de i1 a i3, tal como se muestra en el pasaje del punto “a” al punto “b”.
23
Macroeconomía I
Este pasaje de “a” a “b” se puede ver en el gráfico IS-LM como un desplazamiento vertical y
paralelo hacia abajo de la función LM a LM’ en este caso, a igual renta, Y1, la tasa de interés ha
experimentado una reducción de i1 a i3.
Es en este punto donde el mercado de dinero se halla en equilibrio, pero no lo hay en el
mercado de bienes, el que presenta un desequilibrio caracterizado por un exceso de demanda de
bienes (dado que el punto “b” se halla a la izquierda y por debajo de la función IS). Las razones
del mismo radican en que, al haber disminuido el tipo de interés de equilibrio, la demanda de
inversiones aumentará. Y este aumento desplazará hacia arriba la demanda global en forma
paralela, de DG1 a DG2, generando una nueva renta de equilibrio, Y2. Este punto se exhibe
como “c” en el gráfico del mercado de bienes (por encima del gráfico IS-LM).
C
I
G
DG2
DG1
c
a
Y
i
M0
M1
i
LM
LM’
a
a
i1
i2
i3
c
c
∆M/h
b
L
b
L’
IS
L
Y1
Y2
Y
Cuadro 8.27 – Expansión monetaria en IS-LM
Este aumento en la demanda de bienes (y el consecuente aumento en la renta de equilibrio de
Y1 a Y2) incrementará la demanda de dinero de L a L’ (en una proporción determinada por “k”
multiplicado por el aumento de renta) y presionará al alza la tasa de interés en el mercado
monetario, hasta encontrar su equilibrio en el valor i2, generando un equilibrio en el mercado de
dinero caracterizado por el punto “c”.
En consecuencia, el nuevo valor de la renta de equilibrio será Y2, y el tipo de interés será i2,
consistente con el punto “c”. Este punto se correlaciona con su homónimo en el gráfico IS-LM.
Así, el par de valores (Y2, i2) será el nuevo equilibrio de ambos mercados, que se caracteriza por
reflejar un aumento parcial en la renta de equilibrio y una disminución parcial en el tipo de
interés de equilibrio.
Se puede comprobar que el aumento en la renta será mayor cuanto más aplanada sea la
función IS; esto es, que los valores finales se acerquen más a la solución keynesiana tradicional,
23
Macroeconomía I
con escaso o nulo descenso en la tasa de interés por sobre i1. Este caso extremo podría estar
representado por el punto “d” del gráfico IS-LM. Por el contrario, la política logrará un aumento
escaso en la renta si el tipo de interés disminuye drásticamente y la renta no lo hace, lo que
sería consecuencia de una función IS excesivamente empinada. El caso extremo de esta
situación sería el punto “b” en el cuadro IS-LM.
37.4. Politica monetaria contractiva: emisión de bonos
Consideraremos una contracción monetaria, originada en una emisión de bonos de deuda
pública, adquiridos por el público a cambio de dinero que se retira de la circulación. Este
objetivo también podría ser alcanzado por cualquiera de las herramientas que generan una
disminución en la base monetaria. Se espera que este cambio origine un aumento en la tasa de
interés, que se espera tenga consecuencias en la demanda de bienes.
C
I
G
DG1
DG2
a
c
Y
i
M1
M0
i
LM’
LM
b
i2
b
c
c
i3
i1
a
a
L’
L
IS
L
Y3
Y1
Y
Cuadro 8.28 – Contracción monetaria en IS-LM
Partimos de un equilibrio original IS, materializado en el mercado de bienes como el equilibrio
de la demanda global DG1 en su intersección con la línea auxiliar de 45 grados (sucedáneo de la
oferta de bienes), en el punto “a”, y un equilibrio original LM materializado en el mercado de
dinero como la intersección entre la oferta monetaria M0 y la demanda monetaria L, en el punto
“a”. Ambos equilibrios se expresan en el gráfico IS-LM en un punto designado asimismo con la
letra “a”. La renta de equilibrio original es Y1 y la tasa de interés original de equilibrio es i1.
Una contracción monetaria originada, por ejemplo, en una emisión de bonos del gobierno
adquirida por los particulares, provocará una reducción en la oferta monetaria de M0 a M1, la
que enfrentada a una demanda monetaria L, provocará un incremento en el tipo de interés de i1
a i2, tal como se muestra en el pasaje del punto “a” al punto “b”.
Macroeconomía I
23
Este pasaje de “a” a “b” se puede ver en el gráfico IS-LM como un desplazamiento vertical y
paralelo hacia arriba de la función LM a LM’ en este caso, a igual renta, Y1, la tasa de interés ha
experimentado un aumento de i1 a i2.
Es en este punto donde el mercado de dinero se halla en equilibrio, pero no lo hay en el
mercado de bienes, el que presenta un desequilibrio caracterizado por un exceso de oferta de
bienes (dado que el punto “b” se halla a la derecha y por encima de la función IS). Las razones
del mismo radican en que, al haber aumentado el tipo de interés de equilibrio, la demanda de
inversiones disminuirá. Y esta disminución desplazará hacia abajo la demanda global en forma
paralela, de DG1 a DG3, generando una nueva renta de equilibrio, Y3. Este punto se exhibe
como “c” en el gráfico del mercado de bienes.
Esta caída en la demanda de bienes (y la consecuente reducción en la renta de equilibrio de Y1 a
Y3) reducirá la demanda de dinero de L a L’ (en una proporción determinada por “k”
multiplicado por la disminución de la renta) y presionará a la baja la tasa de interés en el
mercado monetario, hasta encontrar su equilibrio en el valor i3, generando un equilibrio en el
mercado de dinero caracterizado por el punto “c”.
En consecuencia, el nuevo valor de la renta de equilibrio será Y3, y el tipo de interés será i3,
consistente con el punto “c”. Este punto se correlaciona con su homónimo en el gráfico IS-LM.
Así, el par de valores (Y3, i3) será el nuevo equilibrio de ambos mercados, que se caracteriza por
reflejar una baja parcial en la renta de equilibrio y un aumento parcial en el tipo de interés de
equilibrio.
Se puede comprobar que la disminución en la renta será mayor cuanto más aplanada sea la
función IS; esto es, que los valores finales se acerquen más a la solución keynesiana tradicional,
con escaso o nulo descenso en la tasa de interés por sobre i1. Este caso extremo podría estar
representado por el punto “d” del gráfico IS-LM. Por el contrario, la política logrará un descenso
escaso en la renta si el tipo de interés aumenta drásticamente y la renta no se modifica, lo que
sería consecuencia de una función IS excesivamente empinada. El caso extremo de esta
situación sería el punto “b” en el cuadro IS-LM.
37.5. Políticas fiscal y monetaria simultáneas: gasto financiado con emisión
Un caso interesante de la estática comparativa es el ensayo del gasto público financiado con
emisión de dinero por igual cuantía. En este caso, se planea contrarrestar los efectos negativos
de la irrupción del estado en la economía con una inyección de dinero que reduciría o anularía
los aumentos previstos en el tipo de interés.
Siendo el escenario “b” el caso típico de una expansión fiscal (dejando inalterada la oferta
monetaria), y “c” el caso típico de una expansión monetaria (dejando inalterada la función IS),
puede apreciarse que la expansión simultánea de ambas expresiones llevará la solución final al
punto “d”. El escenario puede analizarse en forma secuencial y en cualquier orden; así, la
secuencia “abd” representará una expansión fiscal seguida de emisión monetaria, y la secuencia
“acd” representará una expansión monetaria seguida de una expansión fiscal.
En cualquiera de los dos casos, y tal como puede pronosticarse, el punto “d” será el escenario
final de un aumento combinado del gasto público (de IS a IS’) y emisión monetaria (de LM a
LM’). En este caso, los puntos “a” y “d” se hallan alineados de modo tal que la tasa de interés
permanece inalterada en el valor i1, pero cabe constatar que esta solución es poco probable, por
lo que la tasa de interés final podría hallarse ligeramente por encima o por debajo del valor
inicial. El par de valores de equilibrio final es (Y3, i1) en este caso, con las salvedades aquí
descriptas.
Este caso modelo fue incorporado en la práctica por numerosos gobiernos, que hallaron una
herramienta práctica para lograr una máxima expansión de la renta sin impacto sobre el
mercado monetario. Tarde o temprano la experiencia indicaría que la inflación y el pleno empleo
representaron un límite importante al desarrollo indiscriminado de esta política expansiva
combinada.
23
Macroeconomía I
C
I
G
DG3
d
DG2
DG1
c
a
Y
i
M0
M1
i
LM
LM’
b
i3
b
a
d
i1
a
i2
d
c
c
L
L’
L”
IS
L
Y1
Y2 Y3
IS’
Y
Cuadro 8.29 – Expansion fiscal financiada con emisión en IS-LM
37.6. Multiplicadores de la política fiscal y monetaria
Se trata a continuación de analizar los efectos sobre la renta de la política fiscal y monetaria en
un único modelo, que contenga los impactos estático-comparativos de ambas políticas por
separado y en forma conjunta1. Veamos a continuación una presentación simplificada de las
ecuaciones IS y LM que utilizaremos para este fin.
IS simplificada:
Y = Aα @ dαi
`
a
Y = α A @ di
LM simplificada:b
c
M 0 = kY @ hi L0 = 0
Mf
f
f
f
f
f
f
f kf
f
f
0f
i =@ f
+ f
Y
h
h
Reemplazando el valor de la tasa de interés obtenido en LM en la expresión IS, y distribuyendo:
f
g
dM
Mf
kf
f
f
f
f
f
f
f
f
f
f
f
f dk
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
0f
0f
Y=α A + f
@ f
Y = αA + αd f
@ αd f
Y
h
h
h
h
Pasando al miembro de la izquierda los términos en Y:
f
g
dM
dk
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
0f
Y 1+α
= αA + α f
h
h
Despejando Y y sacando “h” como factor común:
1
Adaptado de Dornbusch-Fischer, “Macroeconomía”, Mc Graw Hill.
23
Macroeconomía I
dM
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
0f
αA
+f
α
+f
αdM
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f αAh
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
hf
0f
Y=
= f
dk
f
f
f
f
f
f
f
f
f
h
+
αdk
1+α
h
Por lo que el nivel de equilibrio del ingreso bien podría ser presentado como la resultante de sus
multiplicadores, lo que se obtiene descomponiendo la expresión precedente:
αh
αd
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
Y= f
A+ f
M
h + αdk
h + αdk 0
Con lo que el multiplicador de la política fiscal representa el primer término, y el de la política
monetaria el segundo:
∂Y
αh
f
f
f
f
f
f
f
f
f f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
= f
∂A h + αdk
∂Y
αd
f
f
f
f
f
f
f
f
f
f
f
f
f
f f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
= f
∂M 0 h + αdk
Sea:
1f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
β= f
h + αdk
Con lo que las expresiones antedichas quedan simplificadas como sigue:
∂Y
f
f
f
f
f
f
f
f
f
f
f
f
f
f
= αβd
∂M 0
∂Y
f
f
f
f
f
f
f
f
f
= αβh
∂A
Puede claramente apreciarse que, dadas las constantes “α" y “β", la efectividad del gasto público
depende de la pendiente de la LM, determinada por la pendiente de la demanda especulativa de
dinero, “h”; y la efectividad de la expansión monetaria depende de la pendiente de la función IS,
determinada por la pendiente de la demanda de inversión, “d”.
Los efectos respecto del tipo de interés pueden obtenerse despejando de la expresión original
esta variable:
i =@
M
M
a
f
f
f
f
f
f
f
f
f kf
f
f
f `
f
f
f
f
f
f
f
f
f
f αkA
f
f
f
f
f
f
f
f
f
f
f
f
f
f αd
f
f
f
f
f
f
f
f
f
0f
+ α A @ di = @ 0 +
@
i
h
h
h
h
h
Pasando al otro miembro:
f
g
Mf
αd
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f αAk
f
f
f
f
f
f
f
f
f
f
f
f
f
0f
i 1+ f
=@ f
+ f
h
h
h
Sacando factor común y eliminando “h”:
M
αAk
f
f
f
f
f
f
f
f
f
f f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
0f
@
+f
M
+
αAk
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f @
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
hf
hf
0f
i=
= f
αd
f
f
f
f
f
f
f
f
f
f
f
h
+
αd
1+
h
y por ultimo obtenemos la descomposición del multiplicador:
αk
1f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
i= f
A@ f
M
h + αd
h + αd 0
Sea:
1f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
γ= f
h + αd
Con lo cual la expresión antedicha puede verse de modo simplificado:
i = γαk A @ γM 0
Con lo que se prueba el impacto positivo de los elementos autónomos del gasto (ponderados por
el multiplicador y por “k”) y negativos respecto de la oferta monetaria sobre el tipo de interés.
21
Macroeconomía I
37.7. Cuadro comparativo de valores posibles IS-LM
En el siguiente cuadro auxiliar (Cuadro 8.30) se muestran algunas alternativas estático-comparativas para un modelo IS-LM convencional.
M. Dinero
M. Bienes
Caso
IS
Caso I
Descripción Situación
del caso
original
Variables
Co
50
Io
104
Go
250
A=Co+Io+Go
404
d
800
c = PMgC
0,8
t (%)
25%
Mo
300
Lo
150
k
0,2
h
1000
Caso II
Aumento
consumo
autónomo
de 20
Caso III
Aumento
inversión
autónoma
de 10
Caso IV
70
104
250
424
800
0,8
25%
300
150
0,2
1000
50
114
250
414
800
0,8
25%
300
150
0,2
1000
50
104
270
424
800
0,8
25%
300
150
0,2
1000
Expansión
fiscal de
20
A/(1-c(1-t))
d/(1-c(1-t))
(Lo-Mo)/h
k/h
1.100,00
2.000,00
-0,15
0,0002
1.150,00
2.000,00
-0,15
0,0002
1.200,00
2.000,00
-0,15
0,0002
1.150,00
2.000,00
-0,15
0,0002
Ye
ie
Renta eq.
Tasa eq.
1.000,00
5,00%
1.035,71
5,71%
1.071,43
6,43%
1.035,71
5,71%
C
I
G
T
Yd
T-G
Consumo
Inversión
Gasto Gob.
Impuestos
Y disponible
Sup. Fiscal
650,00
100,00
250,00
250,00
750,00
-
698,85
99,23
250,00
262,02
786,06
12,02
664,42
109,62
250,00
256,01
768,03
6,01
678,85
99,23
270,00
262,02
786,06
-7,98
Mo
Lt
Oferta Mon.
Dem. Trans.
300,00
200,00
300,00
209,62
300,00
204,81
300,00
209,62
Le
Dem. Espec.
100,00
90,38
95,19
90,38
LM
Caso V
Inversión
más
inelástica
(menor d)
Caso VII
Caso VIII
Caso IX
Caso X
Aumento
Aumento Expansión Gasto fi-.
oferta de
nanc. con de fondos
Aumenta
tasa de
impuestos dinero de emisión
espec. de
PMgC
30
(mayor c) (mayor t) 30
por 20
Tabla de parámetros y variables exógenas
50
50
50
50
50
50
104
104
104
104
104
104
250
250
250
250
270
250
404
404
404
404
424
404
200
800
800
800
800
800
0,8
0,9
0,8
0,8
0,8
0,8
25%
25%
30%
25%
25%
25%
300
300
300
330
320
300
150
150
150
150
150
180
0,2
0,2
0,2
0,2
0,2
0,2
1000
1000
1000
1000
1000
1000
Ecuaciones IS y LM
1.100,00
1.353,85
1.000,00
1.100,00
1.150,00
1.100,00
500,00
2.461,54
1.818,18
2.000,00
2.000,00
2.000,00
-0,15
-0,15
-0,15
-0,18
-0,17
-0,12
0,0002
0,0002
0,0002
0,0002
0,0002
0,0002
Renta y tasa de interés de equilibrio
1.068,18
1.154,64
933,33
1.042,86
1.064,29
957,14
6,36%
8,09%
3,67%
2,86%
4,29%
7,14%
Valores resultantes de las variables del mercado de bienes
630,00
873,46
560,88
653,46
681,15
646,54
86,67
96,48
101,40
102,31
100,77
97,69
250,00
250,00
250,00
250,00
270,00
250,00
241,67
304,99
273,68
251,44
262,98
248,56
725,00
914,96
638,60
754,33
788,94
745,67
-8,33
54,99
23,68
1,44
-7,02
-1,44
Valores resultantes de las variables del mercado de dinero
300,00
300,00
300,00
330,00
320,00
300,00
193,33
243,99
182,46
201,15
210,38
198,85
106,67
Caso VI
56,01
117,54
128,85
109,62
101,15
Caso XI
Aumento
demanda
transacc.
(mayor k)
Caso XII
Caso XIII
Emisión
Trampa de de bonos
liquidez
públicos
(mayor h) por 50
Caso XIV
Reducción
déficit
fiscal de
20
50
104
250
404
800
0,8
25%
300
150
0,25
1000
50
104
250
404
800
0,8
25%
300
150
0,2
2500
50
104
250
404
800
0,8
25%
250
150
0,2
1000
50
104
230
384
800
0,8
25%
300
150
0,2
1000
1.100,00
2.000,00
-0,15
0,00025
1.100,00
2.000,00
-0,06
0,00008
1.100,00
2.000,00
-0,1
0,0002
1.050,00
2.000,00
-0,15
0,0002
933,33
8,33%
1.051,72
2,41%
928,57
8,57%
964,29
4,29%
644,29
96,19
250,00
247,62
742,86
-2,38
653,54
102,36
250,00
251,48
754,43
1,48
644,23
96,15
250,00
247,60
742,79
-2,40
621,15
100,77
230,00
237,98
713,94
7,98
300,00
247,62
300,00
201,18
250,00
198,08
300,00
190,38
52,38
98,82
51,92
109,62
21
Macroeconomía I
38. Modelo IS-LM dinámico
Resulta interesante estudiar una adaptación dinámica2 sencilla del modelo IS-LM, a través del
siguiente grupo de ecuaciones representativas del mercado de bienes:
d
C t = C 0 + cY t
I t = I 0 @ dit
T t = tY t
[1]
d
Y t = Y t @T t
Se caracteriza un desfasaje temporal a través de la siguiente ecuación que muestra la brecha de
producción:
Y t = Ct@ 1 + It@ 1 + G0
[2]
En cuanto al mercado de dinero, tenemos:
s
Mt =M0
t
M d = kY t + L0 @ hit
s
[3]
d
Mt =Mt
Retrasando un período las ecuaciones del mercado de bienes, y sustituyendo las mismas en la
ecuación que muestra la brecha de producción, tenemos:
d
Y t = C 0 + cY t @ 1 + I 0 @ dit @ 1 + G 0
Y t = C 0 + cY t @ 1 @ ctY t @ 1 + I 0 @ dit @ 1 + G 0
`
a
Y t = C 0 + c 1 @ t Y t @ 1 + I 0 @ dit @ 1 + G 0
[4]
A continuación retrasaremos la ecuación del mercado de dinero en un período y la igualaremos
a la oferta monetaria:
M 0 = kY t @ 1 + L0 @ hit @ 1
[5]
Resolveremos el valor de la tasa de interés para esta expresión:
it @ 1 =
Lf
@
M
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f kf
f
f
f
0f
0f
+ Yt@1
h
h
[6]
Reemplazamos este valoren la ecuación [4], y obtenemos una ecuación en diferencias en Y:
F Lf
G
@
M
`
a
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f kf
f
f
0f
0f
Y t = C0 + c 1 @ t Y t@ 1 + I0 @ d f
+ f
Yt@ 1 + G0
h
h
[7]
Agrupando y ordenando, y haciendo que A contenga la totalidad de los elementos autónmos del
gasto, es:
F `
G
Lf
@
M
a dk
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
0f
0f
[8]
Yt = A + c 1 @t @ f
Yt@1@ d f
h
h
De este modo, conociendo el valor de Y para un único lapso, y dados los parámetros “c”, “d”, ‘k”,
”h” y “t” y las variables exógenas o autónomas, podrán conocerse los valores de Y para todos los
períodos siguientes, usando la expresión [8].
Un valor estable para la renta implicará:
@
Y = Y t = Y t @ 1 = Y t @ 2 = …A
[9]
Por lo que la expresión [8] puede formularse de la siguiente manera:
2
Adaptado de Warren Smith, “Macroeconomía”, Edit. Amorrortu.
23
Macroeconomía I
F `
f
g
G@
Lf
@
M
dk
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
0f
Y= c 1@t +
Y+ A@d 0
h
h
@
a
Lf
@
M
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
0f
0f
A
@
df
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
h
D
E
Y=
`
a dk
1 @ c 1 @ t + fffffffff
h
[10]
@
Podemos definir la variable yt-i como el desvío entre el valor corriente del producto para cada
período y el valor de equilibrio:
@
yt = Y t @ Y
@
y t @ 1 = Y t @ 1 @Y
[11]
@
y t @ 2 = Y t @ 2 @Y
@
y t @ i = Y t @ i @Y
Restando la ecuación [10] de la [9], es:
Gb
@ F `
a dk
@c
f
f
f
f
f
f
f
Y t @Y = c 1 @ t @ f
Y t@1 @Y
h
F `
a
G
dk
f
f
f
f
f
f
f
yt = c 1 @ t @ f
y
h t@1
F `
a
[12]
Como regla general, puede determinarse que, para varios períodos, tenemos:
yt = c 1 @ t @
F `
G
dk
f
f
f
f
f
f
f
f
yt @ 1
h
a
yt @ 1 = c 1 @ t @
…
F `
G
dk
f
f
f
f
f
f
f
f
yt @ 2
h
[13]
t
G
dk
f
f
f
f
f
f
f
f
y0
yt = c 1 @ t @
h
a
Por lo que conociendo el valor de Y0 inicial, pueden determinarse todos los valores Yt de los
períodos sucesivos para t=1, t=2, etcétera.
El sistema será estable si:
F `
G
a dk
f
f
f
f
f
f
f
c 1@t @ f
<1
h
[14]
Dado
B C que si se cumple tal condición, necesariamente se verificará que:
@
Yt
=Y
[15]
tQ1
También es cierto, derivando de [14], que:
`
a
dk
f
f
f
f
f
f
f
c 1 @ t <1 + f
h
[16]
Y esta expresión tiene la importante implicancia de que el modelo será estable, aun en el caso de
que la propensión marginal a gastar fuera mayor que la unidad. Sólo debe cumplirse que sea
menor al término de la derecha de la expresión [16], que es claramente mayor que la unidad.
Suponer que la propensión marginal a gastar fuera mayor que la unidad implicaría admitir que
la función IS tiene pendiente positiva. Esto tiene aún otras consecuencias. La pendiente de las
expresiones IS y LM son (considerando la tasa de interés como variable dependiente):
23
Macroeconomía I
`
a
1f
@
cf
1f
@
tf
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
=@
dY IS
d
dr
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f kf
f
f
f
=
dY LM h
dr
f
f
f
f
f
f
f
f
f
f
f
f
f
f
[17]
i
LM
Si transformamos convenientemente [16], es:
`
a
dk
f
f
f
f
f
f
f
c 1 @ t @ 1< f
h
`
a
1f
@
cf
1f
@
tf
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f kf
f
f
@ f
< f
d
h
dr
dr
f
f
f
f
f
f
f
f
f
f
f
f
f
f f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
f
< f
dY IS dY LM
[18]
IS
Y
Cuadro 8.31 – IS-LM dinámico
De lo antedicho, se puede extraer la siguiente conclusión:
La pendiente de IS podría ser positiva, pero se requiere
que tenga menor valor absoluto que la pendiente de LM.
Bibliografía básica
Dornbusch - Fischer, "Macroeconomía" – McGraw-Hill.
Sachs - Larrain. "Macroeconomía en la economía global" – Prentice-Hall.
Bibliografía adicional
Mankiw, Gregory, “Macroeconomia” – Antoni Bosch Editores.
Dernburg – Mc Dougall, “Macroeconomia” – McGraw-Hill
Smith, Warren, “Macroeconomia” – Amorrortu.